箔条弹的投放决策研究

，

(1.海军驻苏州地区通信军事代表室， 江苏苏州 215000；2.海军驻嘉兴地区通信军事代表室， 浙江嘉兴 314033)

0 引言

现代战争中，空空导弹的过载远远超过了飞机，单纯靠机动，飞机几乎没有摆脱导弹的可能。因此在飞机受到雷达制导导弹的威胁时，一般需要投放箔条弹对其进行干扰，而如何投放箔条干扰诱饵才能使干扰效果达到最佳至关重要，这就需要正确地确定干扰诱饵的投放参数和投放时机，这将决定战场上作战飞机的生存率和作战效能[1-2]。投放参数主要包括箔条弹数、弹间隔、组数、组间隔等。这个方向已经有很多人研究[3-4]，但研究条件太过理想。本文以前人的研究为基础，考虑更全面的限制条件，例如，在研究弹间隔时考虑了反射截面积的变化情况，给出了更符合实际的研究结果。

1 箔条干扰的原理及过程

箔条质心干扰是机载箔条在实战中的一种有效应用干扰方式，它的物理基础是雷达的空间跟踪点位于其分辨单元的能量中心上，当分辨单元内存在一个目标时，雷达跟踪该目标的能量散射中心[5]；当雷达分辨单元存在两个或两个以上的目标时，雷达则跟踪由这几个目标散射能量中心构成的共同的能量中心。按照这个原理，通过打箔条的方法，在被压制雷达天线方向的一定范围内设置一个假目标，并使得之后形成箔条云的雷达有效反射截面积大于飞机的雷达有效反射截面积，从而使雷达跟踪点偏离飞机，而飞机则乘机迅速机动飞出雷达的分辨单元，摆脱雷达的跟踪。随着雷达技术的发展，当飞机移出导弹的跟踪单元之后，导弹跟踪目标点的速度发生突变，导弹的末制导雷达将会发现飞机已经逃逸，这样雷达会从跟踪状态转入到搜索状态，直至再次转入跟踪，如此往复，直到导弹击中目标或自爆。

2 箔条干扰弹的投放参数

2.1 弹间隔

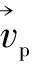
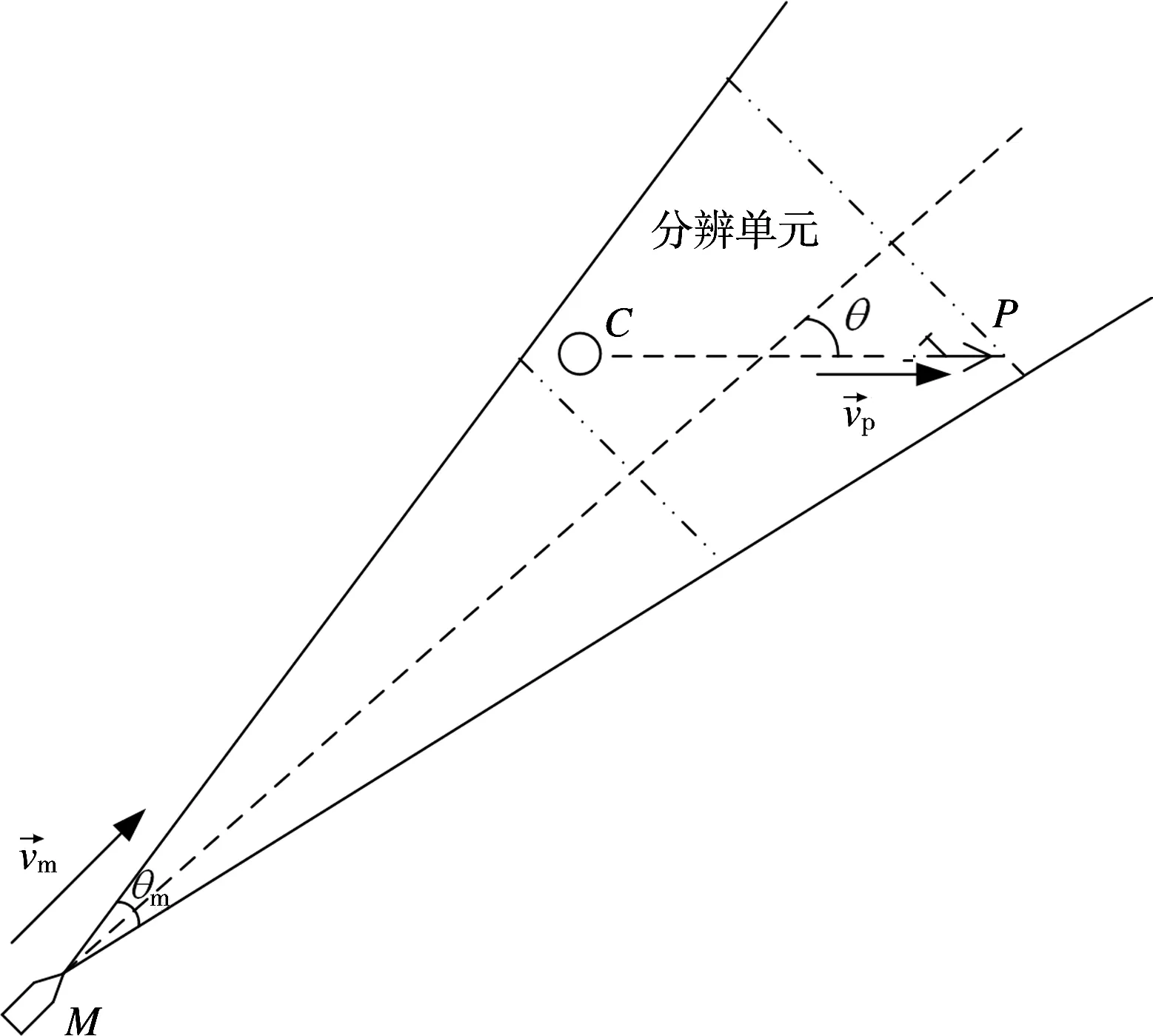
图1 箔条诱饵干扰导弹末制导雷达

由图1可知，飞机通过导弹末制导雷达距离分辨单元所用的时间为

(1)

式中，τ为雷达脉冲宽度，c为光速。

飞机通过末制导雷达的角度分辨单元所用的时间为

(2)

式中，R为导弹距飞机的距离。

(3)

如果在一个分辨单元内投放多发箔条干扰弹，那么就需要考虑箔条诱饵的发射截面积随时间的变化，然而要精确给出箔条云团的散射截面积是十分困难的，根据其散开情况进行分析，可用瑞利曲线来模拟箔条播撒后箔条云团反射截面积随时间的变化情况[6]，可表示为

(4)

式中，d为瑞利分布的参数，反映箔条云有效持续时间。仿真如图2所示。

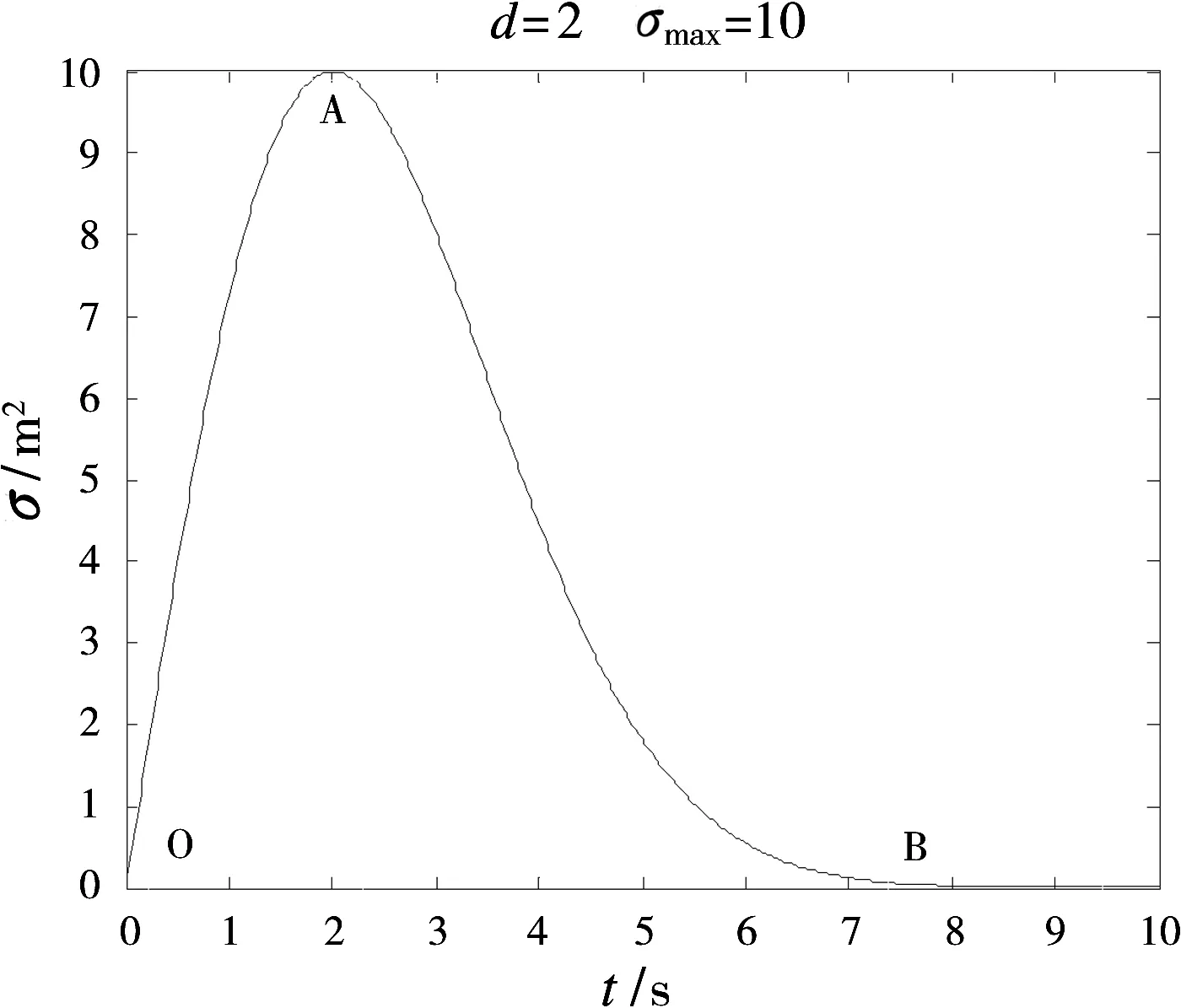
图2 箔条云发射截面积随时间的变化

飞机的反射截面积为Sp，设箔条云的面积必须大于飞机的反射截面积时，质心干扰才真正起到作用，那么给出下面的方程式：

Sc(t)=Sp

(5)

求解可得到两个时间t11和t22，箔条弹的投放间隔与这两个时间密切相关。

如果箔条弹投放时间间隔过短，雷达的导引头将从跟踪两个目标的能量中心转向跟踪3个目标的能量中心，这样第二发箔条弹将会破坏第一发箔条弹的质心干扰，当弹机之间的距离过近时，可能会导致飞机受到攻击；如果投放间隔的时间过长，有一段时间将存在导弹的分辨单元内箔条云的反射截面积小于飞机的反射截面积，导致质心干扰不能真正起到作用，或者飞机已经飞出了导弹的跟踪单元再投放箔条弹导致箔条弹的浪费。

为了使质心干扰发挥最佳的效果，可以适当地选择投放间隔，使第一发箔条质心干扰结束时，第二发箔条的质心干扰恰好发生作用，所以箔条弹的投放间隔可取为

(6)

2.2 箔条弹数

在角度上摆脱导弹威胁的时间为ta：

(8)

设导弹一次威胁攻击的时间Tb，必须满足下面的条件：

Tb≥ta且Tb≥td

(9)

当飞机飞出导弹的距离分辨单元或角度分辨单元之后，一次质心干扰就取得了成功，那么导弹的一个威胁攻击时间为Tb=min(ta,td)。

那么箔条弹数为导弹一次威胁攻击时间与箔条弹间隔之间的比值，即

(10)

当弹数为非整数时，通常向上取整，所以箔条弹数的实际取值为

(11)

2.3 箔条组间隔

一次质心干扰成功后，飞机逃离出导弹的跟踪单元，质心的状态将发生突变，导弹转入搜索状态，当导弹搜索到飞机后，将再次转入到跟踪状态，然后飞机告警，再次实施箔条质心干扰，如此往复[7]。箔条组间隔就是指导弹从失去目标到再次跟踪上目标的这段时间，是末制导雷达从跟踪状态转入到搜索状态，导弹再次捕获到目标和末制导雷达从搜索状态转入到跟踪状态三者所用时间的和。其中两种状态之间的转换时间与末制导雷达本身的特性有关，而导弹再次捕获到目标的时间与导弹和飞机的相对空间位置有关，并且与雷达的扫描方式也有一定的关系。那么箔条组间隔可表示为

Tcg=T1+T2·k(θ,φ)·k+T3

(12)

式中，T1为雷达跟踪转入搜索所用的时间，T2为开始搜索到发现目标所用的最短时间，T3为发现目标到跟踪目标所用的时间，k(θ,φ)为相对空间系数，k为雷达扫描方式对应的系数。

2.4 箔条组数

干扰弹组数是指飞机成功实施干扰所投放箔条的次数，它与导弹和飞机的相对位置、速度、威胁源本身的特性、飞机反射截面积等因素有关。由于箔条弹多组干扰过程中，导弹受到箔条云多次干扰而使导弹的跟踪路线发生变化，而且飞机和导弹间的相对方位也随时间发生变化，所以对箔条组数的求解须在具体条件下给出仿真结果并作分析[8]。在所有的导引方法中，只有平行导引法能够通过几何解算求出弹目相遇时间的解析解，以此为例，如图3所示。

图3 导弹跟踪飞机

由余弦定理得到下面的方程式：

(13)

式中，rMP为飞机初被跟踪时弹机的距离，rPP′为导弹命中目标时飞机飞行的距离，rMP′为导弹命中目标时导弹飞行的距离，φ为飞机飞行方向与末制导雷达跟踪方向的夹角。

由于导弹和飞机均看作匀速直线运动， 那么

(14)

(15)

其中，rMP为已知。通过上面3式求解可以得出相遇时间tmeet：

(16)

如果导弹采用其他的引导方法，tmeet的值就必须通过仿真的方法解算出。以导弹采用比例导引法为例，在给出上述条件的基础上，设定比例导引系数，那么通过仿真可以得出结果，如图4所示。

(b)弹目之间的距离差图4比例导引法下导弹跟踪飞机

由图4(b)很容易看出在相应仿真条件下的弹目相遇时间tmeet，由此可以更准确地估计出弹目的相遇时刻，对结合实际情况估计箔条弹的组数更有帮助。

箔条弹投放测组数为

(17)

同样，组数也应向上取整，所以实际中Ncg的取值为

(18)

3 箔条投放时机

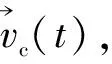
(19)

飞机在垂直方向上距质心的距离为

(20)

图5 导弹转向跟踪质心

由于导弹的转弯角速度不是很大，且转入跟踪箔条云的时间很短，仍假设箔条云作直线运动，在这段时间内导弹的位移为

(21)

所以此时导弹距飞机的位移近似为

(22)

导弹从跟踪飞机转入跟踪质心的过程中，导弹转过的角速度对应的弧长为

(23)

考虑到导弹转过的角度很小，其对应的弧度可近似等于lpc，表示为

(24)

4 实例分析

飞机速度vp=400 m/s，导弹速度vm=800 m/s，导弹角度分辨率θm=3°，飞机运动方向与导弹来袭方向的夹角θ=15°，导弹和飞机距离r=1 000 m，末制导雷达脉冲宽度τ=0.6 μs，不考虑箔条弹的散开过程，且箔条弹的反射截面积与飞机的反射截面积之比为Sc∶Sp=4∶1。末制导雷达跟踪转入搜索的时间和发现目标转入跟踪的时间均为0.1 s，开始搜索到发现目标所用的最短时间为0.05 s，相位相对系数为1.5，雷达扫描方式对应的系数为2。

在如上的条件下，代入推导公式得出弹间隔和一次威胁时间分别为

Tcb=min(tr,tan)=0.232 9 s

Tb=min(ta,tb)=0.582 3 s

由此可以推导箔条弹数为

组间隔为

Tcg=0.1+0.05×1.5×2+0.1=0.35 s

假设导弹采用比例导引式，则由仿真结果得到弹目相遇时间为

tmeet=1.93 s

则箔条组数为

5 结束语

在现代战争中，突防飞机往往不能携带足够多的箔条干扰诱饵，所以箔条弹投放参数和投放时机的选择对箔条质心干扰的效果有着十分重要的影响，正确地选择投放参数和时机既不会导致箔条干扰诱饵的浪费，又提高了箔条干扰的效率。本文结合实际的情况，计算出了箔条投放的各参数和时机，对箔条的投放有一定的参考意义。

[1] 才干. 机载无源干扰技术应用的研究[D]. 西安：西北工业大学, 2007.

[2] 蒋志彪,骆鲁秦,李鑫,等. 机载箔条弹投放系统作战效能评估[J]. 雷达科学与技术, 2013, 11(3):246-250.

JIANG Zhibiao, LUO Luqin, LI Xin, et al. Operational Effectiveness Evaluation of Airborne Chaff Cartridge Delivery Subsystem[J]. Radar Science and Technology, 2013, 11(3):246-250.(in Chinese)

[3] 赵恩起,牛继涛. 质心干扰中机载红外弹、箔条弹投放间隔时间的讨论[J]. 光电对抗与无源干扰, 2002(3):19-22.

[4] 才干. 直升机机载无源干扰的战术算法研究[J]. 光电对抗与无源干扰, 2000(2):27-31.

[5] 冯云松,郭宇翔. 雷达箔条的战术应用及发展趋势[J]. 飞航导弹, 2012(12):54-57, 61.

[6] 胡华强,徐忠伟. 机载箔条弹最佳使用时机仿真研究[J]. 航天控制, 2008, 26(4):61-64.

[7] 李海浩,李海涛,李宁龙. 箔条质心干扰仿真模型研究[J]. 电子信息对抗技术, 2010, 25(1):52-55.

[8] 杨超. 箔条特性对投放战术的影响[J]. 光电技术应用, 2013, 28(2):80-82.