基于OMP算法的极化敏感阵列多参数估计

， ，

(电子科技大学电子工程学院， 四川成都 611731)

0 引言

压缩感知(Compressive Sensing, CS)[1]是近几年提出的一种稀疏信号重构技术，它突破了奈奎斯特采样定理对采样频率的制约，可以以低频率进行欠采样，然后以高概率、高精度重构原始信号，降低数据采样、存储和处理的成本。CS理论为开辟高性能DOA估计算法提供了良好思路，但目前CS理论在多参数估计方面仍然存在比较大的问题。

对极化敏感阵列的研究自20世纪90年代开始日趋活跃，并成为阵列信号处理研究的新热点[2]。其中对目标的DOA和极化参数估计一直都是研究的重点，而与常规标量阵列相比，利用矢量阵列可以进行多参数的估计，包括功率、极化参数等。多重信号分类[3](MUSIC)算法的提出使得高分辨测向技术发展有了飞跃性的突破。但是，对于多参数估计，传统的MUSIC算法需要进行多维谱峰搜索，计算量太大，文献[4-5]提出模值约束求解极化参数，降低了运算量，但在相干信号情况下估计失效。文献[6]提出了通过旋转不变性进行信号参数估计(ESPRIT)算法，避免了空间谱峰搜索，解决了运算量和储存量方面的问题，但相干信号情况下失效。而将压缩感知理论应用于矢量阵列参数估计时，其表现出的少快拍、低信噪比条件下仍有较好性能，以及天然的解相干能力等优势，是传统DOA估计算法不具备的，因此利用压缩感知理论进行矢量阵列DOA估计，具有十分重要的意义。

标量阵列下压缩感知理论已经有了比较成熟的研究，文献[7-8]分别提出了L1-SVD算法以及L1-SRACV算法，文献[9-10]提出加权范数算法，三者都属于凸松弛算法，信号分辨率高，但运算复杂度大。文献[11]在凸松弛算法的基础上提出了将极化信号分解并利用LASSO算法求解极化参数的算法，得到比较精确的DOA估计，但极化参数估计结果并不好，并且算法涉及到正则化参数的选择，计算复杂度非常高。文献[12]提出了标量阵列下的正交匹配追踪算法OMP算法，相对于L1-范数算法，OMP算法的优点是计算量小，并能够更多地运用在实际工程中。本文在OMP算法的基础上，对极化敏感阵列信号观测矩阵重新建模，将空域与极化域参数分离进行估计，首先利用改进的OMP算法得到空域到达角估计结果，在已知空域到达角估计结果的基础上，利用模值约束构造代价函数计算得到极化域参数估计结果，将空域和极化域分离处理，达到了降维的目的，减小了算法计算量。与传统的MUSIC算法以及ESPRIT算法不同，该算法不需要求解协方差矩阵，进行特征值分解，这使得该算法在相干信号情况下同样适用，同时也在一定程度上减少了算法运算复杂度。本文算法在小快拍数的情况下估计性能相较于ESPRIT算法以及模值约束MUSIC算法也有比较明显的优势。

1 常规OMP算法求解DOA

考虑均匀线性阵列，阵元数为M， 阵元间距为d， 均匀线性阵列空间导向矢量为

as(θ,φ)=[1,e-jφ,…,e-j(M-1)φ]T

(1)

式中，φ=2πdsinθsinφ/λ，λ为波长。为方便且不失一般性，假设信源方位角φ=90°。为得到波达方向估计，将整个空间的方位角划分为Nθ份，构造M×Nθ维的冗余字典：

(2)

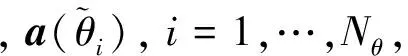
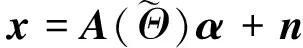
(3)

式中，x和n分别为阵列各通道的接收矩阵和其中的噪声，均为M×N维，α为Nθ×1维的稀疏向量，只有信号入射方向对应的位置非零，其余位置全为零。上述稀疏表示模型对应的稀疏重构问题可以写为

(4)

1) 初始值设置：残差R0=x，原子集合A0为空矩阵，原子指针集Γ0为空，迭代次数k=0；

4) 计算最小二乘问题s′k=arg max‖x-Aks′‖2，并更新残差Rk=x-Aksl；

5)如果k=K那么结束迭代，得到K个信号的DOA估计，否则k=k+1重复步骤2)。

OMP算法属于压缩感知重构方法中贪婪算法的一种，相较于凸优化算法虽然精度稍有欠缺，但运算复杂度小，因此更多的运用在实际工程中。本文中选择OMP算法对极化敏感阵列模型进行求解。

2 极化敏感阵列信号模型

为了将标量阵列下的OMP算法运用到极化敏感阵列信号多参数估计中，进行如下信号建模。对于完全极化波，考虑一个由M个天线单元所组成的极化敏感均匀线性阵列，阵元间距为d，以及K个远场窄带极化信源。对应的极化矢量可以表示为

ap(θ,φ,γ,η)=V(θ,φ)·E(γ,η)=

(5)

式中，γ∈[0,π/2)为极化幅角，η∈[-π,π)为极化相角，θ∈[-π/2,π/2]和φ∈[0,2π)分别为空域俯仰角和空域到达角。为推导方便且不失一般性，假设空域角度φ=90°，那么极化矢量ap(θ,φ,γ,η)退化为

ap(θ,γ,η)=V(θ)·E(γ,η)=

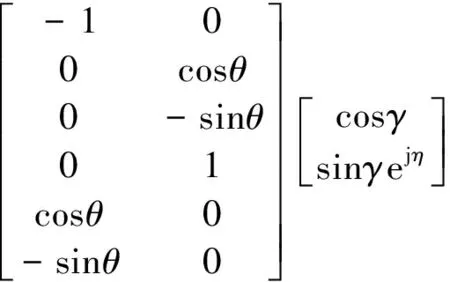
记api为极化矢量ap(θ,γ,η)中对应的每一行的元素值。极化敏感阵列的导向矢量可以表示为极化矢量与空域导向矢量的Kronecker积，即

as,p(θ,γ,η)=ap(θ,γ,η)⊗as(θ)

(7)

式中，as(θ)=[1,e-jφ,…,e-j(M-1)φ]T，φ=2πdsinθ/λ，λ为波长。第k个信号的接收模型可以表示为

xk(t)=as,p(θk,γk,ηk)sk(t)+nk(t)

(8)

将上述极化敏感阵列信号接收模型对应行相加可以表示为

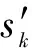
(9)

x′=As′+n′

(10)

x′=A(Θ)α+n′

(11)

观察式(11)和式(3)可以发现，此时的极化敏感阵列是可以采用OMP算法求解的。

3 改进的OMP算法及极化参数求解

3.1 改进的信号波达方向估计算法

RK-1=x′-AK-1s′K-1

(12)

那么最小二乘问题的解为

[(AK-1)HAK-1]-1(AK-1)Hx′

(13)

将x′及式(10)代入式(9)，可以得到下面的形式：

RK-1=(I-AK-1((AK-1)HAK-1)-1(AK-1)H)·

(14)

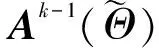
4) 计算最小二乘问题s′k=arg max‖x′-Aks′‖2，并更新残差Rk=x′-Aks′l；

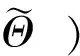
6) 如果k=K那么结束迭代，得到K个信号的DOA估计，否则k=k+1重复步骤2)。

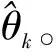
3.2 极化参数的估计

极化敏感阵列导向矢量如式(7)中所示，证明得到

as,p(θ,γ,η)=ap(θ,γ,η)⊗as(θ)=

(V(θ)⊗as(θ))·E(γ,η)

(15)

式中，as,p(θ)=V(θ)⊗as(θ)。由上节步骤2)中的原子选择准则可以看到，信号到达角方向与残差的相关性最大。同样，在得到DOA的估计结果后，极化敏感阵列信号导向矢量与观测矩阵的相关性最大，这样可以得到极化参数的估计结果。那么求解极化参数就可以转换为如下问题：

s.t.‖E(γ,η)‖=1

(16)

式中，x为观测矩阵，as,p为极化导向矢量。

(‖xH(as,p(θ)E(γ,η))‖1)2=

(xH(as,p(θ)E(γ,η)))H(xH(as,p(θ)E(γ,η)))=

E(γ,η)Has,p(θ)HxxHas,p(θ)E(γ,η)

(17)

式中，

G(θ)=as,p(θ)HxxHas,p(θ)

(18)

那么式(16)就变成如下问题：

maxE(γ,η)HG(θ)E(γ,η) s.t. |E(γ,η)|2=1

(19)

G(θ)E(γ,η)=uE(γ,η)

(20)

为解决上式的问题，建立代价函数：

L(θ,γ,η)=EH(γ,η)G(θ)E(γ,η)-

u[EH(γ,η)E(γ,η)-1]

(21)

对式(21)关于E(γ,η)求梯度，并令结果等于0，得到

(22)

即G(θ)E(γ,η)=uE(γ,η)

(23)

可以看出，E(γ,η)为G(θ)的特征值u所对应的特征向量，因为

EH(γ,η)G(θ)E(γ,η)=uEH(γ,η)E(γ,η)=u

(24)

所以，要使得EH(γ,η)G(θ)E(γ,η)最大，相当于要求得最大的u。而G(θ)的最大特征值对应的特征向量正好是E(γ,η)，即

E(γ,η)=vmax[G(θ)]

(25)

(26)

(27)

3.3 基于OMP算法的极化敏感阵列多参数估计算法步骤

1) 将极化敏感阵列信号接收矩阵按照式(9)、(10)中所示的形式进行建模；

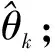
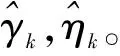
3.4 算法复杂度分析

算法的运算量主要与M,N,K和n有关，其中M代表阵元个数，N代表采样快拍数，K代表入射信号个数，n代表搜索范围内点数。通常情况下，M,N和K都比n小得多，所以算法的运算量主要取决于与n有关的项。在计算入射信号的波达方向时，本文算法构造了冗余字典，模值约束MUSIC算法运用谱峰搜索，都与搜索范围点数n有关，但本文算法不需要求解协方差矩阵，同时也不需要对协方差矩阵进行特征值分解，相对模值约束MUSIC算法，复杂度小。对于极化ESPRIT算法，算法不需要进行谱峰搜索，因此算法运算量与n无关，但与模值约束MUSIC算法相同，两者都需要比较大的快拍数才能得到精确的估计结果，而本文算法小快拍下就可以得到良好的估计结果，减少了算法运算量。

4 算法仿真及分析

仿真实验一：假设阵元数M=16，阵元间距d=λ/2，噪声为高斯白噪声，两个入射信号的角度及极化参数分别为(θ1,γ1,η1)=(10°,15°,30°)， (θ2,γ2,η2)=(60°,45°,75°)，两个信号非相干情况下进行实验。改变采样快拍数，信噪比为5 dB，每个快拍条件下进行500次蒙特卡罗实验，图1(a)、(b)、(c)分别给出了在小快拍情况下极化ESPRIT算法、模值约束MUSIC算法、本文的入射信号波达方向估计及极化参数估计的均方误差曲线。从仿真结果可以看出，随着快拍数的增加，误差减小，对于信号到达角的估计，本文算法在快拍数小于17 dB时，性能比ESPRIT以及MUSIC算法好，这表现出压缩感知小快拍下性能优越的特点。极化参数估计方面，本文算法优于ESPRIT和模值约束MUSIC算法。

仿真实验二：改变入射信号的信噪比，快拍数为50，进行500次蒙特卡罗实验，两个信号非相关条件下进行实验，其余仿真条件与实验一中相同。图2(a)、(b)、(c)分别给出了极化ESPRIT算法、模值约束MUSIC算法、本文的入射信号波达方向估计以及极化参数估计的均方根误差曲线。从仿真结果可以看出，随着信噪比增加，均方根误差越来越小。对入射信号的到达角估计，本文算法在信噪比小于0 dB时优势明显，随着信噪比的增加MUSIC算法的估计性能优势凸显出来，这是因为MUSIC算法在求解DOA时运用特征分解，在大信噪比时优势明显。两者的估计结果都优于ESPRIT算法。极化参数的估计本文算法总体优于极化ESPRIT算法和模值约束MUSIC算法，从图1(b)中可以看到在信噪比增大到16 dB左右ESPRIT和模值约束算法的性能要比本文算法好，这也是由于两种算法都运用了特征值分解而带来的优势。

仿真实验三：入射信号的信噪比为10 dB，快拍数为200，两个信号相干情况下进行实验，其他实验条件与实验一中相同，进行500次蒙特卡罗实验仿真得到统计均方根误差对比结果如表1所示。从仿真结果可以看出，本文算法在相干信号情况下可以进行工作，但模值约束MUSIC算法及ES-PRIT算法已经失效，不能够进行多参数的估计。所以将压缩感知运用于极化敏感阵列中，无论在相干信号还是非相干信号的情况下都能够得到良好的估计结果。

(a)到达角估计误差随快拍变化

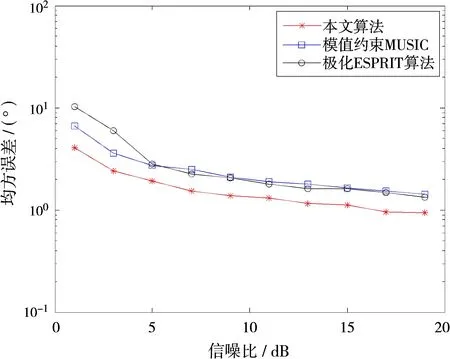
(b)极化幅角估计误差随快拍变化

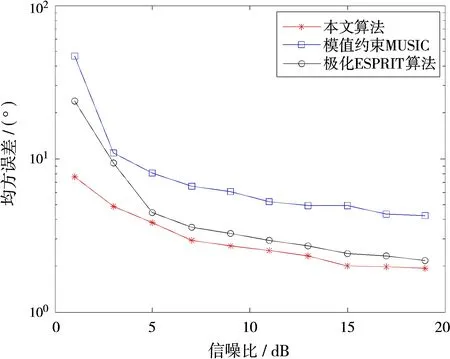
(c)极化相角估计误差随快拍变化图1估计误差随快拍变化曲线

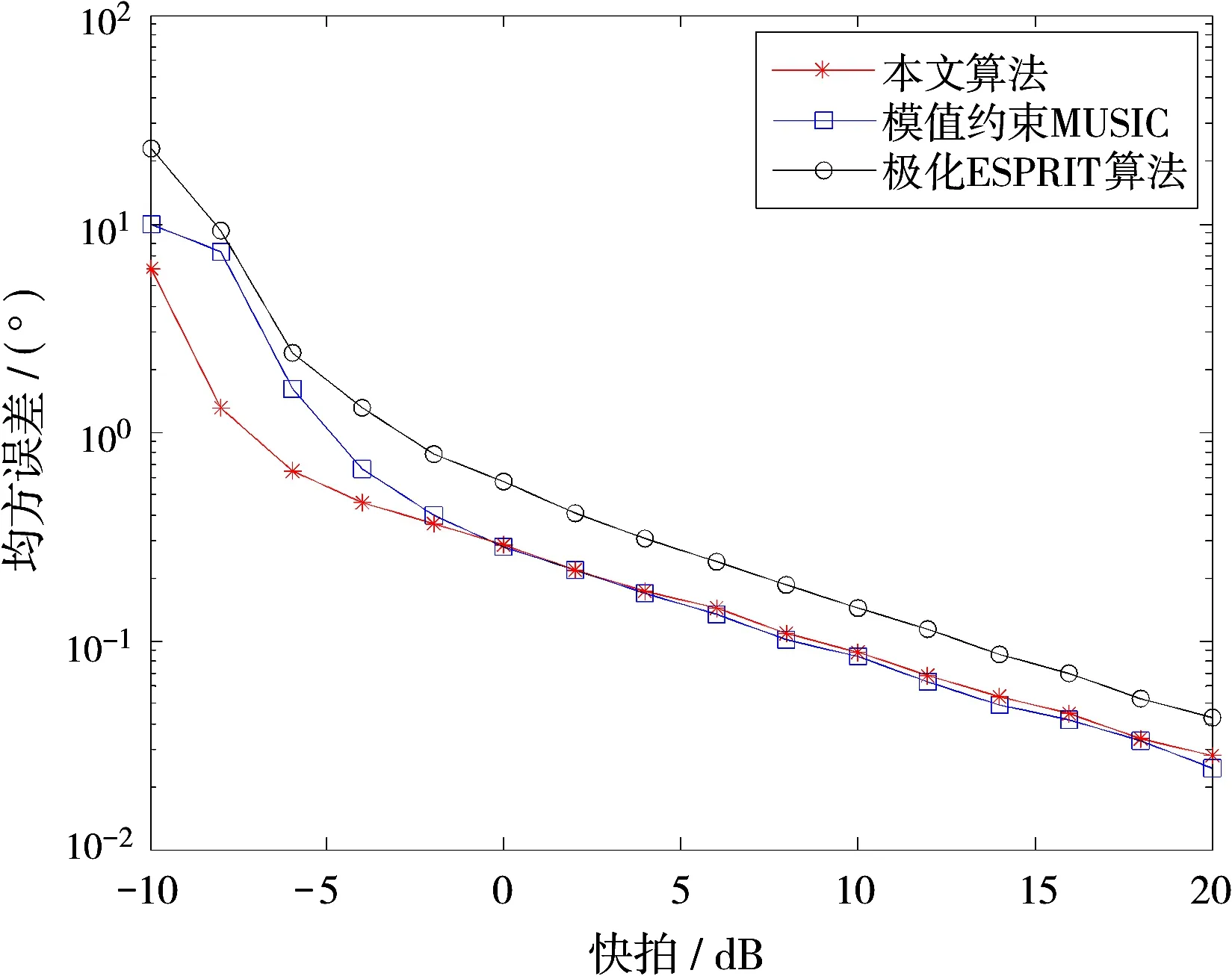
(a)到达角估计误差随信噪比变化

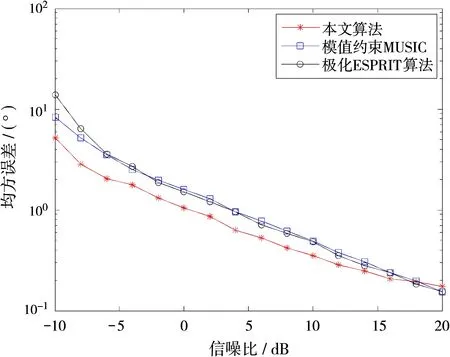
(b)极化幅角估计误差随信噪比变化

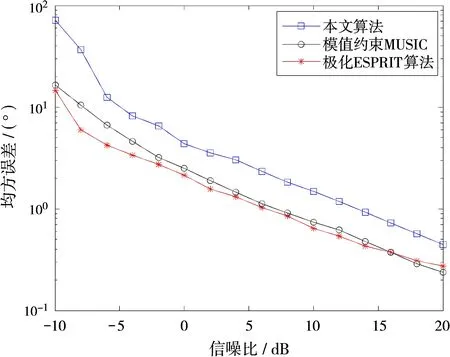
(c)极化相角估计误差随信噪比变化图2估计误差随信噪比变化曲线

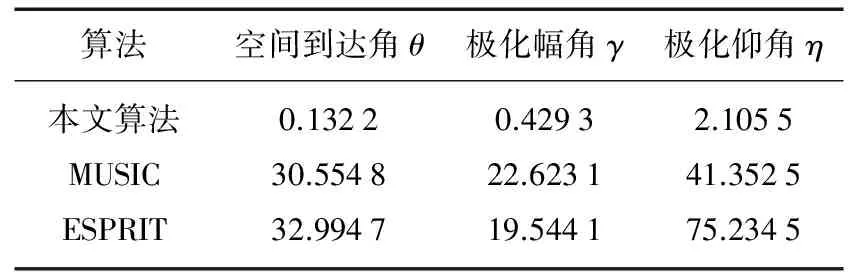
表1 统计均方根误差结果对比

注：表中的MUSIC算法为模值约束MUSIC算法。

5 结束语

本文研究压缩感知理论在极化敏感阵列信号多参数估计中的应用，在OMP算法的基础上，提出一种改进的极化OMP算法。算法对极化敏感阵列信号观测矩阵重新建模，将空域与极化域参数分离进行估计，达到了降维以及独立估计的目的。与传统的MUSIC算法以及ESPRIT算法不同，算法不需要求解协方差矩阵，进行特征值分解，这使得算法在相干信号情况下同样适用，同时也在一定程度上减少了算法运算复杂度。本文算法在小快拍数的情况下估计性能相较于ESPRIT算法以及模值约束MUSIC算法也有比较明显的优势。通过仿真验证了算法的正确性以及性能的优越性。通过与传统的ESPRIT算法以及模值约束MUSIC算法的仿真性能对比，也可以看到将压缩感知理论运用在极化敏感阵列多参数估计中能够达到比传统极化方法更好的估计性能。并且本文算法在小快拍及低信噪比时性能更好，具有很好的估计效果以及较快的收敛速度。

[1] DONOHO D L. Compressed Sensing[J]. IEEE Trans on Information Theory, 2006, 52(4):1289-1306.

[2] 庄钊文,徐振海,肖顺平. 极化敏感阵列信号处理[M]. 北京：国防工业出版社, 2006:199-263.

[3] SCHMIDT R O. Multiple Emitter Location and Signal Parameter Estimation[J]. IEEE Trans on Antennas and Propagation, 1986, 34(3):276-280.

[4] LI Huiyong, ZHANG Yuanfang, XIE Julan. A Reduced-Dimensional Music Algorithm with Modulus Constraint Based on Electromagnetic Vector Sensor Array[C]∥Asia-Pacific Signal and Information Processing Association Annual Summit and Conference, Hong Kong:APSI PA, 2015:328-332.

[5] 张远芳,周正,李会勇. 极化敏感L型阵模值约束的多参数联合估计[J]. 雷达科学与技术, 2016, 14(1):81-85.

ZHANG Yuanfang, ZHOU Zheng, LI Huiyong. Multi-Parameters Estimation for L-Shaped Polarization Sensitive Array Using the Modulus Constraint[J]. Radar Science and Technology, 2016, 14(1):81-85.(in Chinese)

[6] OH D, LI Y, KHODJAEV J, et al. Joint Estimation of Direction of Departure and Direction of Arrival for Multiple-Input Multiple-Output Radar Based on Improved Joint ESPRIT Method[J]. IET Radar, Sonar and Navigation, 2015, 9(3):308-317.

[7] MALIOUTOV D, CETIN M, WILLSKY A. A Sparse Signal Reconstruction Perspective for Source Localization with Sensor Arrays[J]. IEEE Trans on Signal Processing, 2005, 53(8):3010-3022.

[8] YIN J, CHEN T. Direction-of-Arrival Estimation Using a Sparse Representation of Array Covariance Vectors[J]. IEEE Trans on Signal Processing, 2011, 59(9):4489-4493.

[9] 田野,孙晓颖,秦宇镝. 基于两步加权L1范数约束的高分辨率波达方向和功率估计[J]. 电子与信息学报, 2014, 36(7):1637-1641.

[10] 刘福来,彭泸,汪晋宽,等. 基于加权L1范数的CS-DOA算法[J]. 东北大学学报(自然科学版), 2013, 34(5):654-657.

[11] TIAN Ye, SUN Xiaoying, ZHAO Shishun. Sparse-Reconstruction-Based Direction of Arrival, Polarisation and Power Estimation Using a Cross-Dipole Array[J]. IET Radar, Sonar and Navigation, 2015, 9(6):727-731.

[12] TROPP J A, GILBERT A C. Signal Recovery from Random Measurements via Orthogonal Matching Pursuit[J]. IEEE Trans on Information Theory, 2007, 53(12):4655-4666.