巧用课堂生成,演绎精彩课堂
2016-03-09周艳娟
周艳娟
[摘要]本文由一个发生在公开课上的真实案例,从把握课堂中的“意外”生成,激发学生的学习潜能,点拨课堂中的“错误”生成,化课堂生成为一次新的学习,直面课堂中的“非预设”生成,冷静处理化尴尬为精彩.本文从三个方面来谈如何巧用课堂生成,演绎精彩课堂.
[关键词]课堂生成;演绎;精彩课堂
在我们的数学课堂教学中总是孕育着许多非预期性的因素,教师常常会遇到这样的情形:学生对一个问题的回答,或是小组讨论所得的结果,或是针对教学内容提出的疑问等偏离了教师预设的“轨道”.这时,教师往往感觉难以应对,一来担心在课堂上出现科学性错误;二来担心耽误了时间,无法完成教学任务.因此,对之要么视而不见,要么置之不理,要么暂时回避(留作课后讨论),要么生硬地将学生的思路拉回“预定轨道”.久而久之,就会让学生感受到课堂上的讨论是“假讨论”,课堂上的探究是“假探究”,从而失去对数学学习的热情和兴趣,变得不愿想、不愿说、不愿做.
有一个发生在公开课教学中的真实案例:上课老师在讲完“负负得正”的法则后,让学生计算(-3)×(-4)=?,学生甲回答是9,教师让他坐下,另一位学生乙回答是12,教师再请学生乙说出算法依据.下课后一位听课的教研员与学生甲交流,才让学生甲有机会讲出自己的思考:在数轴上,站在-3这个点上,因为是乘-4,所以要沿着数轴向反方向——右方移4次,每次移动3格,结果是9.对于这个案例有不少文章已进行了讨论,不少文章大都从数学角度来分析解决学生甲发生的错误,而这则案例却引发了笔者对课堂生成方面的一些思考.
把握课堂中的“意外”生成,激发学生的学习潜能
人文主义心理学指出:限制和顺从不能养成创造性,权威主义的教育只能造就驯服,而不是有创造性的学生.因此,教师不要把学生当作部属来对待,不要忘记学生也是一个“人”,应当尊重学生的情感和个性,营造一种自由、平等的人文氛围,让学生获得生动、和谐的发展.首先,教师要从神圣的三尺讲台上走下来,到学生中去,做学生的朋友.学生“只有卸下心理上的包袱,才会迸发出创造的潜能”.在这种自由平等的氛围中,学生才会敢想、敢说、敢做,其次,教师要从学生精神生命发展的主宰者的位置上退下来,一改过去无视学生人格,忽视学生差异,指令多、指责多、框框多的做法,容许学生自由活动,容许学生提问质疑,容许学生指出老师的错误,打破教师的“权威”,把学生精神生命发展的主动权还给学生,教师应该认识到:学生是一个学习者,更是一个合作交流、自主探究者,每个学生都有自己的感官和头脑、自己的知识和思想基础、自己的思考方式和行动规律.教师不可能代替学生感知、观察、分析、思考,代替学生明白任何道理和掌握任何规律.因此,出现学生的思维偏离教师的“预设轨道”的情形时,如果教师能把它作为一种资源巧妙地加以利用,则往往能成为教学过程中闪亮的环节.
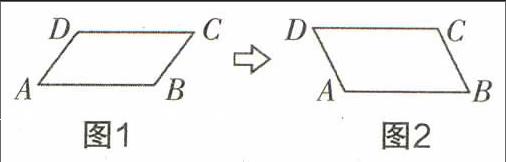
笔者曾上过一堂市级公开课《矩形》,在得到矩形定义这个环节,设置了如下情境:如图,将平行四边形ABCD的边AB固定不动,则从图1到图2的变化过程中,哪些量发生了变化,怎样变化?哪些量保持不变,为什么?
对于这样开放性的问题设计,学生的学习兴趣和热情充分被调动起来了,发言热烈积极,有学生提到面积发生了变化,下面马上有同学反对,笔者立马拿出准备好的教具让学生进行演示.既然学生提到了面积,便顺水推舟提问:在面积变化过程中什么时候面积达到最大?有了刚才的教具演示,学生很快回答出来了,并且有不少学生还能够解释为什么那时面积最大.虽然课堂上多花了几分钟时间,但是不仅让学生加深了对矩形的理解,而且还为学生的后续学习埋下了伏笔,更是锻炼了学生的数学思维能力,
点拨课堂中的“错误”生成,化课堂生成为一次新的学习
古人云:人非圣贤,孰能无过.学生在学习过程中出现错误是在所难免的,课堂中学生出现错误是美丽的,错误其实是孩子们经验最真实的暴露,学生在教师面面俱到、点滴不漏、无微不至的“关怀”和“体贴”下,一帆风顺地朝着教师指引的方向前进,这种教学方式可能一时比较容易让学生尝到“成功”的喜悦,但长此以往只会造成学生的依赖心理,作为高明的教师,不要惧怕学生出现的错误,把错误当成一种难得可利用的生成性资源,加以巧妙运用则可以产生“柳暗花明又一村”,将这些错误生成五彩缤纷的“精彩”,
在上面的案例中,这位学生在老师讲了教材上写的“负负得正、绝对值相乘”法则后,竟然敢于用一个不同的算法来计算,这种独立思考、勇于创新的科学精神,正是我们在当今教育中提倡并在实际教学中努力实践、用心培养的。从该生所得的结果看,是违背了“负负得正、绝对值相乘”的法则,从该生的计算方法看,计算错误的真正原因还是没有理解“负负得正”的道理.在数轴上规定向右运动为正,那么(一3)×(-4)中的-3代表的不是表示一3的点,而是表示从原点向左移动3个单位;乘-4就是从原点(而不是-3在数轴上的点)向反方向(右)运动四次共十二个单位,第一个负号代表向左运动,第二个负号表示沿相反方向运动,而运动的起点是原点.这不正是学生最容易产生困惑、教学的重难点之处吗?因此在教学中,教师不必回避学生的错误算法,而应该引导全体学生讨论这个错误的算法,然后点化其错误之处,让该生的错误算法成为帮助全体学生理解“负负得正”的有益素材,转化为全体学生的一次新的学习,
锁定“错误”的目的是为了放大生成,不仅解决了所生成的问题,还让学生在思辨、修正和提升中获得深刻的情感体验和广泛的活动经验,使学习过程充满着激情与活力,
直面课堂中的“非预设”生成,冷静处理化尴尬为精彩
叶澜教授指出“教学过程中教师要把学生看作教学资源的重要构成和生成者,教师是课堂教学过程中呈现信息的重组者”.而传统教学条件下,教师个人知识不是那么外显,教师只要具备本学科的专业知识外,大可高枕无忧,因为一切都是预设的,绝不节外生枝,但在新课程条件下,课堂是开放的、是生成的.要科学而艺术地把握课堂教学中的预设与生成需要教师有高超的教学智慧.endprint
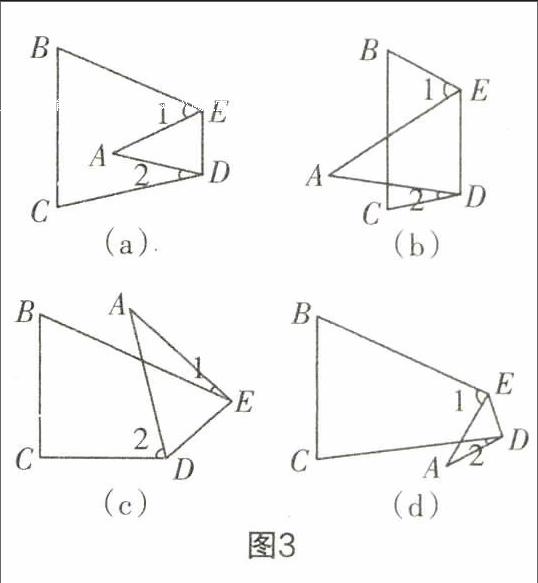
在一次练习课上,有这样一道题:如图3,把△ABC纸片沿DE折叠,使点A落在四边形BCDE的内部.∠A与∠l+∠2之间存在怎样的数量关系?请试着找出来,并说明理由.
为了解决这个问题,笔者先给出两个特殊化的条件:①∠B=50°,∠C=70°;②∠B=40°,∠C=60°,学生很快便求出了∠A以及∠1+∠2的度数,并且发现了它们之间的关系为∠1+∠2=2∠A.根据上面的解题思路,学生给出了答案.正当笔者准备为本题做一个小结的时候,有位学生竟然提出了这样一个问题:如果点A在四边形BCDE的边上或者外部,这个结论还成立吗?
面对这样的提问,笔者毫无心理准备,很想把这个问题放到课后去解决,但转念一想或许当堂解决会有意想不到的收获.于是,迅速作出反应:这个问题提得很好,请大家讨论讨论.经过全体学生的合作探究,得到以下结果:(1)若点A在四边形BCDE的边上,点A分别在BC,BE,CD上时,∠1+∠2=2∠A仍然成立;(2)若点A在四边形BCDE的外部则有三种情况:①如图(a),∠1+∠2=2∠A成立;②如图(b),解得∠2-∠1=2∠A;③如图(c),解得∠1-∠2=2∠4.这个收获对笔者来说是意外的,同时也给笔者敲响了警钟——平时要深入研究教材,挖掘教材,只有这样才有足够的底气和勇气去面对教学中出现的问题
“生成”对应于“预设”,尽管在课前的设计中,教师对学生可能出现的一些情况作了设想,然而我们面对的毕竟是一个个活生生的学生,有些情况并非我们可以主观臆测的,当课堂中出现这样那样始料未及的尴尬时,教师若装聋作哑,会挫伤学生学习的积极性;若严词斥责,将泯灭学生智慧的火花;若敷衍搪塞,将使学生疑窦倍增,如坠云雾,于是就需要教师能直面尴尬,冷静思考,巧妙捕捉其中的“亮点”资源,从容不迫、胸有成竹面对,在与学生的平等对话与合作中一定会迎刃而解;并灵活地调整教学进程,使课堂在不断“生成”中绽放精彩,
《数学课程标准》也指出:数学是人类的一种文化,它的内容、思想、方法和语言是现代文明的重要组成部分;义务教育阶段的数学课程,其基本出发点是促进学生全面、持续、和谐的发展;使学生获得对数学理解的同时,在思维能力、情感态度与价值观等方面得到进步和发展由此可见,教育的目标蕴含着深刻的人文化倾向,为此,我们必须深刻反思,并努力探索初中数学人文化教育的新途径、新方法.数学课堂教学需要我们直面生成、即兴创作,在教学中我们应该随时关注学生的发展,了解学生在关注什么,需要什么,希望接受什么;审视学生在学习过程中遇到了什么问题,及时优化教学的策略,关注课堂中生命的涌动和成长.endprint
