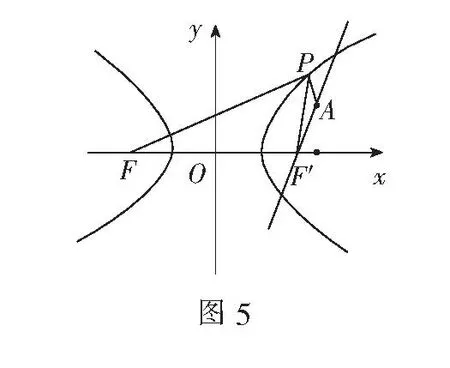
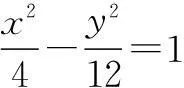一道高考题的解法、推广及启示

2016-03-02杨瑞强

高中数学教与学 2016年1期

关键词：双曲线交点切线

一道高考题的解法、推广及启示

杨瑞强

(湖北省黄石市第一中学,435000)

一、试题呈现(2015年四川高考题)

(1)求椭圆E的方程;

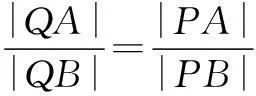
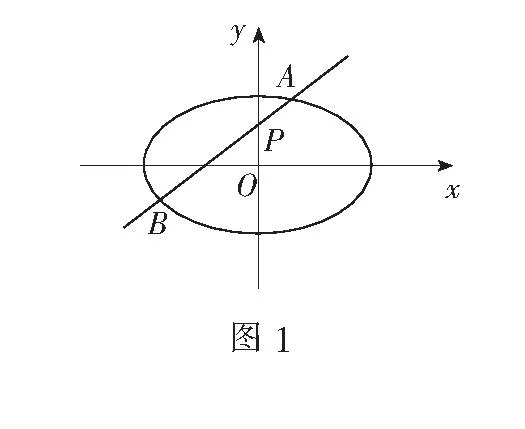
二、试题分析与证明

所以点Q在y轴上,可设Q(0,t).

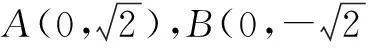
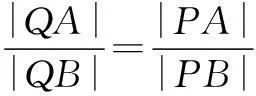
解得t=1或t=2.

所以,若存在与点P不同的定点Q满足条件,则Q点的坐标只可能为Q(0,2).

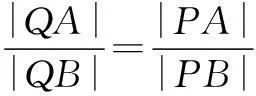
① 当直线l的斜率不存在时,由上可知,结论成立.

② 当直线l的斜率存在时,可设直线l的方程为l:y=kx+1,A(x1,y1),B(x2,y2),其中x1x2<0,y1y2<2,则

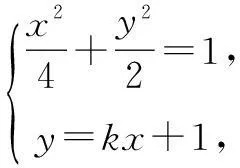
得(2k2+1)x2+4kx-2=0,

因此Δ=16k2+8(2k2+1)>0,

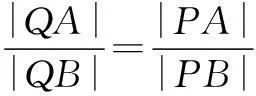
证法1(利用对称性,证明三点共线)

易知,与点B关于y轴对称的点的坐标为B′(-x2,y2).

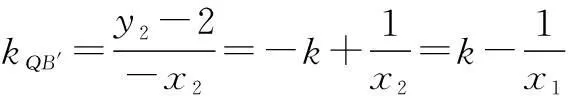
所以kQA=kQB′,即Q,A,B′三点共线(如图2)，

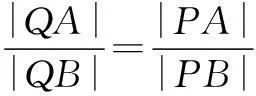
证法2(线段坐标化,代数推理论证)

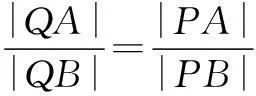
整理，得x2(2-y1)+x1(2-y2)=0,

即x1+x2-2kx1x2=0.

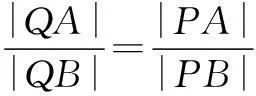
证法3(利用内角平分线定理,证明斜率互为相反数)

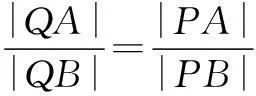
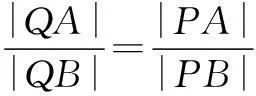
证法4(利用伸缩变换,将椭圆变圆)

由l的两种特殊位置:x=0和y=1,可求出Q(0,2).(具体过程同上)

由OA′2=OB′2=2=OP′·OQ′知,直线OA′、OB′分别是∆P′A′Q′、∆P′B′Q′外接圆的切线.

因为∠OA′P′=∠OB′P′,所以由弦切角与圆周角的关系，知∠P′Q′A′=∠P′Q′B′,从而

tan∠P′Q′A′=tan∠P′Q′B′,

即∠PQA=∠PQB,

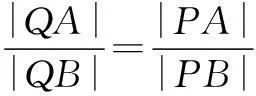
三、试题推广

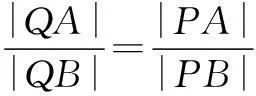
由OA′2=OB′2=OP′·OQ′知,直线OA′、OB′分别是∆P′A′Q′、∆P′B′Q′外接圆的切线.

因为∠OA′P′=∠OB′P′,所以∠P′Q′A′=∠P′Q′B′,从而

tan∠P′Q′A′=tan∠P′Q′B′,

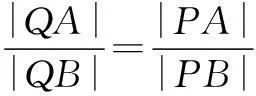
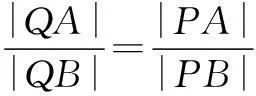
(说明:此处推广命题仅利用伸缩变换证明,也可以利用前三种方法证明,限于篇幅,留给有兴趣的读者自行完成.)

(证明同上,此处略.)

四、试题解法启示

(1)圆锥曲线中的定点(定值)问题,一直是高考的热点问题,解决此类问题常见的方法有两种:一是直接推理、计算,并在推理计算的过程中消去变量,从而得到定点(定值);二是从特殊位置入手,求出定点(定值),再证明这个点(值)与变量无关.前者研究一般情形,通过逻辑推理与计算得到定点(定值),这种方法难度大,运算量大,且思路不好寻找;后者就是先利用特殊情况确定定点(定值),然后验证.

(2)在解决解析几何问题时,学生偏重于相关量的数量关系研究,习惯于代数的严密推理过程,而忽视了有关形的知识的应用,导致计算量很大.事实上,若能充分把握解析几何问题中形的特征,注意挖掘隐蔽条件,灵活运用平面几何知识,对于拓宽解题思路,减少运算量,将会起到非常重要的作用.比如在本文的高考试题中,学生如果能发现此比例关系是角平分线定理,那么求解起来会相当轻松.因此,在求解解析几何问题时,要重视平面几何知识的运用,细心观察,敢于联想,从而发现重要关系,为解决问题开辟道路.

(3)从变换的角度看,把圆“压”一下即成椭圆,椭圆也可以再“伸”一下还原成圆.在研究直线与椭圆的位置关系的问题时,利用伸缩变换将椭圆转化为圆后,往往可以避免联立方程组这一繁琐的程序,而将问题转化到直线与圆的位置关系这一大家非常熟悉的问题中来,使得原来隐于椭圆内的一些几何关系,得以显性化，然后可以利用圆的有关性质加以解决,从而达到简化运算的目的.

高三数学综合测试

一、填空题(本大题共14小题,每小题5分,共70分)

1.已知集合A={x||x|≤2},B={x|3x-2≥1},则A∩B=______.

3.命题“∀θ∈R,sinθ≤1”的否定是______.

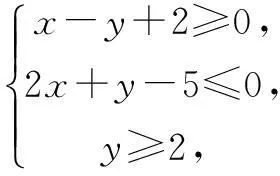
11.若x轴是曲线f(x)=lnx-kx+3的一条切线,则k=______.

12.已知定点M(-1,2),动点N在单位圆x2+y2=1上运动,以OM，ON为邻边作平行四边形OMPN,则点P到直线3x+4y+10=0距离的取值范围是______.

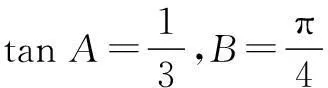
14.实数a、b、c满足a2+b2+c2=5,则 6ab-8bc+7c2的最大值为______.

二、解答题(本大题共6小题,共计90分,解答时应写出文字说明、证明或演算步骤)

15.(本小题满分14分)设函数

(1)求f(x)的单调增区间;

(2)若x∈(0,4),求y=f(x)的值域.

(1)求角C的大小；

(2)若a2=2b2+c2,求tanA的值.

(1)若椭圆C的右准线方程为x=4,求椭圆C的方程；

18.(本小题满分16分)有一块三角形边角地,如图中∆ABC，其中AB=8(百米)，AC=6(百米)，∠A=60°.某市为迎接2500年城庆,欲利用这块地修一个三角形形状的草坪(图中∆AEF)供市民休闲,其中点E在边AB上，点F在边AC上，规划部门要求∆AEF的面积占∆ABC面积的一半，记∆AEF的周长为l(百米).

(1)如果要对草坪进行灌溉,需沿∆AEF的三边安装水管,求水管总长度l的最小值;

(2)如果沿∆AEF的三边修建休闲长廊,求长廊总长度l的最大值,并确定此时E、F的位置.

(1)求圆C的方程；

(2)过原点O作圆C的两条切线，与抛物线y=x2相交于M、N两点(异于原点).证明：直线MN与圆C相切；

(3)若抛物线y=x2上任意三个不同的点P、Q、R，且满足直线PQ和PR都与圆C相切，判断直线QR与圆C的位置关系，并加以证明.

20.(本小题满分16分)已知函数

f(x)=|x3-1|+x3+ax(a∈R).

(1)解关于字母a的不等式

[f(-1)2]≤f(2);

(2)若a<0,求f(x)的最小值；

(3)若函数f(x)有两个零点x1,x2,试判断f(x1x2)的符号，同时比较f(x1x2)与a+1的大小，并说明理由.

参考答案

一、填空题

1.[1,2];2.2;3.∃θ∈R,sinθ>1;

二、解答题

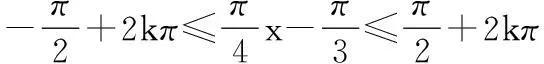
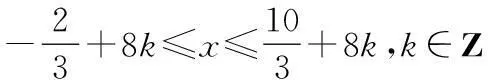
∴f(x)的单调增区间为

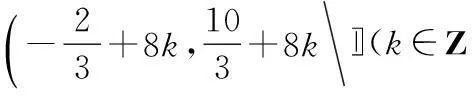
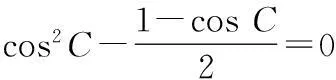
整理得 2cos2C+cosC-1=0,

∵a2=2b2+c2,∴a2=2b2+a2+b2-ab.

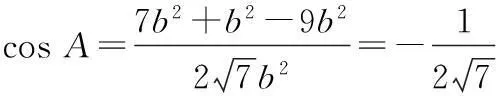
(2)设A(x1,y1),D(x2,y2),则B(-x1,-y1),

∵A,D在椭圆上，

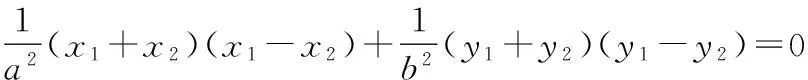
18.(1)设AE=x(百米)

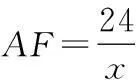
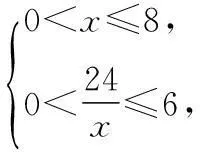
∵∆AEF中，

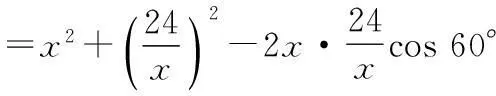
列表

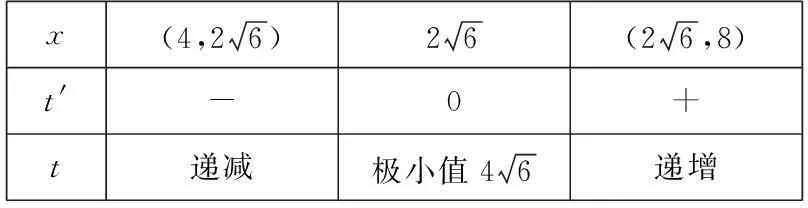
x(4,26)26(26,8)t'-0+t递减极小值46递增

且x=4时，t=10;x=8时，t=11,则

∴当t=11时，lmax=18,此时AE=8,AF=3.

19.(1)∵C(0,2),∴圆心C到直线x-2y+2=0的距离

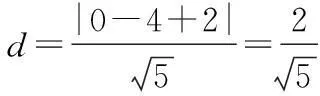
∴圆C的方程为x2+(y-2)2=1.

(2)设过原点的切线方程为

y=kx,即kx-y=0,

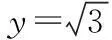
∵圆心C(0，2)到直线MN的距离为1，且r=1,∴直线MN与圆C相切.

(3)直线QR与圆C相切.证明如下：

设P(a,a2),Q(b,b2),R(c,c2),则直线PQ、PR、QR的方程分别为

PQ：(a+b)x-y-ab=0,

PR:(a+c)x-y-ac=0;

QR:(b+c)x-y-bc=0.

∵PQ是圆C的切线，

化简得(a2-1)b2+2ab+3-a2=0.

①

∵PR是圆C的切线，同理可得

(a2-1)c2+2ac+3-a2=0.

②

则b,c为方程(a2-1)x2+2ax+3-a2=0的两个实根，

∵圆心到直线QR的距离

∴直线QR与圆C相切.

20.(1)∵[f(-1)]2≤f(2),

∴(1-a)2≤15+2a,

即a2-4a-14≤0,

(2)∵f(x)=|x3-1|+x3+ax

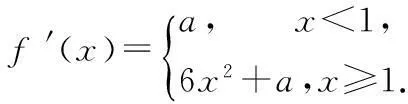
∴当x<1时，f′(x)<0,当x>1时，f′(x)>0,∴f(x)在(-∞,1)上单调减，在(1,+∞)上单调增，故函数f(x)有最小值f(1)=a+1.

综上可得

(3)由(2)知，当a≥0时，f′(x)>0,函数f(x)在R上单调递增,至多只有一个零点,不合题意.

当-1≤a<0时，f(x)min=a+1≥0，不可能有两个零点.

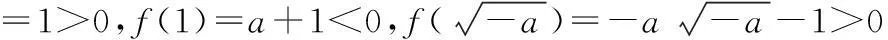
∴x1

又f(x)在(0,1)上单调递减，

∴f(1)

即a+1

○短文集锦○

探究双曲线中一类最值的求法

张云霄李光记

(河南省濮阳市综合高中，457000)

我们知道,双曲线上一点到它的一个焦点与另一定点的距离之和或差的最值问题,是双曲线问题的常见题型．本文对这类问题进行分类讨论,研究其解法,供读者参考．

解如图1,设F′是双曲线的右焦点,由定义得

|PF|=|PF′|+4，

所以|PF|+|PA|≥4+|F′A|=4+5=9.

当且仅当P为线段F′A与双曲线右支的交点时，|PF|+|PA|取得最小值9.

评注上述解法用到了以下方法:① 用定义,把到左焦点的距离转化为到右焦点的距离;② 若A、B为定点,P为不同于A、B的任意一点,则|PA|+|PB|≥|AB|,当且仅当P在线段AB上时,|PA|+|PB|取得最小值|AB|．

一、变换结论进行探究

解|PF|-|PA|=4+|PF′|-|PA|.

因为|PA|-|PF′|≤|AF′|=5，

所以|PF′|-|PA|≥-|AF′|=-5,

从而|PF|-|PA|≥4-|AF′|=-1.

当且仅当P为线段AF′的延长线与右支的交点时,等号成立.

二、变换条件进行研究

解如图4,与上面的题不同的是点A在右支弧内,结合图形分析,知

解如图5,|PF|-|PA|=4+|PF′|-|PA|，又-|AF′|≤|PF′|-|PA|≤|AF′|,即 2≤|PF|-|PA|≤6.由于直线AF′与双曲线右支有两个交点,所以当且仅当P为线段F′A的延长线与双曲线右支的交点时,|PF|-|PA|取到最大值6,当且仅当P为线段AF′的延长线与双曲线右支的交点时,|PF|-|PA|取到最小值2．