函数零点问题的常见处理策略
2016-03-02臧华
函数零点问题的常见处理策略
臧华
(江苏省泰州市姜堰区蒋垛中学,225503)
在学习过程中学生经常会碰到函数零点问题.虽然命题类型不多,但是难度颇大.如果学生解题方法掌握不到位,解题时往往感到束手无策.解决函数的零点问题,通常有以下处理策略.
一、求解型
这类问题通常是研究函数零点的个数和确定零点所在区间,或者已知函数的零点个数或零点所在区间求参数的取值范围.处理的方法有两类:一类是直解型,另一类是图象型.
例1函数
的零点为______.
分析两段函数均可以直接解出零点,需要注意的是定义域的限制.
解当x≤0时,由x2-2x-3=0,得x=3(舍去),x=-1;当x>0时,由-1+lnx=0,得x=e,所以函数f(x)的零点分别为-1和e.
评注函数y=F(x)有零点等价于方程F(x)=0有实数根.当函数是一元二次函数或者是基本初等函数时,函数的零点可以直接解出.



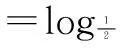
评注函数y=F(x)=f(x)-g(x)有零点也等价于函数y1=f(x),y2=g(x)图象有交点.
当函数是一元二次函数和基本初等函数的组合时先判断函数是否单调:如果单调且连续,可以用零点存在性定理检验零点的情况;如果不单调,可以先令函数等于0,移项后再作出两个函数的图象,研究它们的交点情况.
变式训练函数f(x)=lnx+2x-5的零点个数为______(答1个).
例3已知a是实数,函数f(x)=2ax2+2x-3-a.如果函数y=f(x)在区间[-1,1]上有零点,求实数a的取值范围.
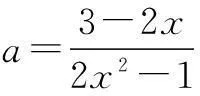
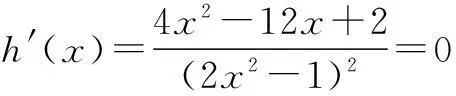

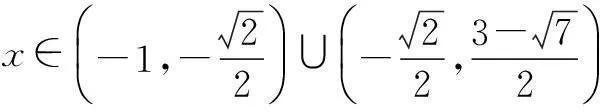

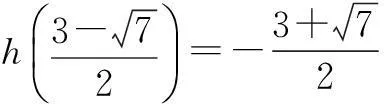



评注对于已知函数零点个数求参数的取值范围,首先变量分离,分离后方法如下:
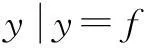
(2)方程f(x)=a在区间I上的零点数⟺y=f(x)与y=a的图象在区间I上的交点数.
例4已知二次函数f(x)=x2+2bx+c(b,c∈R)满足f(1)=0,且关于x的方程f(x)+x+b=0的两个实数根分别在区间(-3,-2)、(0,1)内,求实数b的取值范围.
分析先利用f(1)=0得到c关于b的表达式,进而构造函数g(x),再利用根与系数的关系求解.
解由题知,f(1)=1+2b+c=0,∴c=-1-2b.
记g(x)=f(x)+x+b=x2+(2b+1)x-b-1,则

评注对于不方便变量分离的问题,可利用根与系数的关系处理.先作出图象,标出区间,写出相应限制条件.

二、求证型
这类问题要证明函数有一个或几个零点,通常处理方法是:零点存在性定理和导数法结合使用.



∴f(2)=a-c.
若c>0,则f(0)f(1)<0,f(x)在(0,1)内有零点;
若c≤0,则f(2)>0,f(1)f(2)<0,f(x)在(1,2)内有零点.
所以函数f(x)在[0,2]内至少有一个零点.
评注利用零点存在性定理确定函数有几个零点,不仅要求函数f(x)在[a,b]上是连续的曲线,且f(a)f(b)<0,还必须结合函数的图象与性质(如单调性).
变式训练求证:函数f(x)=3ax2+2bx+b-a在区间[-1,0]内至少有一个零点.
例6已知函数f(x)=(a-x)ex+1,其中a>0,证明函数f(x)只有一个零点.
分析f′(x)=ex(-x+a-1).于是,可由导数的符号求出函数的单调区间,确定f(a-1)是极大值,也是最大值.再结合函数的解析式特点,判断函数f(x)在区间(-∞,a-1)和(a-1,+∞)内的变化情况,结合函数零点存在性定理加以说明.
解f′(x)=ex(-x+a-1).
令f′(x)=0,解得x=a-1.
因为x∈(-∞,a-1)时,f′(x)>0,x∈(a-1,+∞)时,f′(x)<0.
所以函数f(x)的单调增区间是(-∞,a-1),减区间是(a-1,+∞).
所以f(a-1)是极大值,也是最大值,且
f(a-1)=ea-1+1>0.
① 当x
所以f(x)在(-∞,a-1)上恒为正数,函数f(x)没有零点.
② 当x>a-1时,取x=a+1,则f(a+1)=-ea+1+1.
因为a>0,所以ea+1>e,-ea+1<-e.
从而f(a+1)=-ea+1+1<0.
由零点存在定理可知,在区间(a-1,a+1)上函数f(x)有一个零点.
因为(a-1,+∞)是f(x)的减区间,所以f(x)零点只有一个.
综上,函数f(x)零点只有一个.
解决函数零点个数问题,主要方法有零点存在性定理和图象法.根据函数零点的性质求解参数的取值范围主要有分类讨论、数形结合、等价转换等方法,掌握这些基本方法可以有效解决和零点相关的问题.
