基于APOS 理论的“柯西不等式”教学



○教学研究○

基于APOS 理论的“柯西不等式”教学

席明明

(安徽省安徽师范大学,241000)

APOS理论是由美国数学教育学家杜宾斯基在20世纪80年代提出的一种关于数学知识学习的新理论,是一种具有数学学科特色的建构主义学习理论．这种理论认为,学生学习数学概念必须要经历“操作(Action)”,“过程(Process)”,“对象(Object)”,“图式(Schema)”四个阶段,才能完成知识建构,从本质上掌握知识．根据对APOS理论的理解,笔者设计了以下“柯西不等式”教案，以企抛砖引玉，供同仁们交流探索．

第一阶段观察与操作(操作阶段) ——活动为主的感性认识

问题1你还记得“赵爽弦图”吗?

师:大家还记得图1这幅图吗?它证明了什么结论?(回顾旧知)．

生1:这个是“赵爽弦图”.我们通过面积计算得出,大正方形面积S与小三角形的面积S∆满足S≥4SΔ,得到了基本不等式

师:观察这个图形,它的每个小三角形形状都如何?

生2:四个直角三角形完全相同．

师:假如四个直角三角形是两两相同,用两个红色直角三角形和两个蓝色直角三角形，可以拼出什么样的图形?(让学生自己动手操作,在纸上画出；几分钟后,教师在PPT上给出图2和图3.)

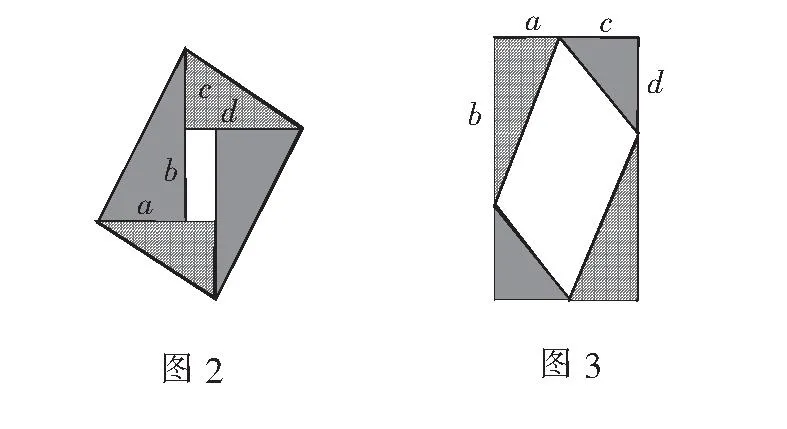
师:令所画红色直角三角形直角边长分别为a,b,蓝色直角三角形的直角边长分别为c,d．大家能否结合图1面积的求法,把图2,图3中的平行四边形面积表示出来？

第二阶段综合分析(过程阶段)——思维活动为主的理性思考

生3:我是结合图1的方法,从外部和内部分别表示这个大平行四边形的面积．设平行四边形一个内角为α,由图3从外部表示为

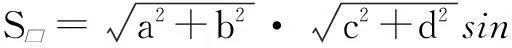
①

另外,由图2知，平行四边形面积又等于2个红色三角形面积加2个蓝色三角形面积再加中间矩形面积，即

=ac+bd.

②

师:那么①②表示的面积是相等的,sinα可以消掉吗?(引导学生用不等式表示面积)

生4:不可以．除非sinα的值为1,即α=90°,0≤sinα≤1．

师:那可以用一个不等式去表示吗?

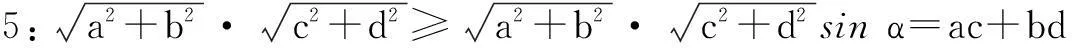
师:能否换一种形式呢?可能将根号去掉?

生6:两边平方，可得

(a2+b2)(c2+d2)≥(ac+bd)2.

③

师:我们把这样的不等式叫做柯西不等式．大家看看图3,你们用上述方法表示出平行四边形面积后,得出了③式吗?

设计意图联立几何图形证明基本不等式,通过平行四边形的面积表示,可引导学生探究出柯西不等式的表达形式．图3的证明可以让学生自己去完成,起到一个巩固的作用．

问题2能用其它方法说明上述不等式成立吗?

师:(a2+b2)(c2+d2)≥(ac+bd)2，你能证明这个不等式吗?(让学生讨论)

生7:我用的是作差法．用不等式的左边减去不等式右边得到a2d2+b2c2-2abcd≥0，即有(ad-bc)2≥0恒成立．所以(a2+b2)(c2+d2)≥(ac+bd)2,当且仅当ad=bc时取等号．

师:很好,这是证明柯西不等式的基本方法之一:作差法．还有别的方法吗?

师:我们一起来看看这个函数 f(x)=a2x2+b2x2-2acx-2bdx+c2+d2≥0恒成立,我们又可以得到什么?

生8:这是关于一个x的二次函数,f(x)≥0恒成立,则Δ≤0．

生9:我由Δ≤0,得到了4(ac+bd)2≤4(a2+b2)(c2+d2),同时约去4,这不就是我们要证明的柯西不等式吗．(全班因得到这个“意外”的结论而欢呼)

问题3探索不等式中等号成立的条件．

师:什么时候我们可以取等号呢?

生10:当且仅当ad=bc时等号成立，从刚刚采用的作差法就可以得到．

生11:我是反过来做的．要证ad=bc,即证(ad-bc)2=0,只要证明a2d2+b2c2-2abcd=0,只要证明a2d2+b2c2-2abcd+a2c2+b2d2=a2c2+b2d2;移项化简得到(ac+bd)2=(a2+b2)(c2+d2)，所以当且仅当ad=bc时等号成立．

问题4柯西不等式是否对任意的实数a,b,c,d是否都成立?(让学生自己验证,由于每项都含有平方项,发现柯西不等式确实对任意的实数都成立.)

评注此过程引导学生证明了柯西不等式,探究了等号成立的条件,从而进一步揭示了柯西不等式的本质．证明的过程联系了旧知,学生也掌握证明不等式的方法(作差法,综合法,分析法)．教师要做充分的预设,对于学生给出预设外的答案,要给于充分肯定,并从容应对解答．

设计意图学生在头脑中对反复的不等式证明活动作出尝试,并不断进行分析、反思,通过思维的内化、整合与压缩,形成过程模式,抽象出柯西不等式的概念,即“活动”内化为“过程”．此时个体能够对柯西不等式的概念进行一般化,认识其实质．由此对知识的认识从感性上升到理性,为第三阶段形成概念做好铺垫．

第三阶段建构阶段(对象阶段)——数学应用与表示

师:对任意的实数a,b,c,d,都有(a2+b2)·(c2+d2)≥(ac+bd)2,当且仅当ad=bc时等号成立，我们把这个不等式叫做柯西不等式．

问题5你能准确地用文字语言表达柯西不等式吗?

师:左边像什么?(平方和相乘)右边又像什么?(积的和的平方)想想在基本不等式中我们如何用文字语言去表达的?

生12:平方和的积大于或等于积的和的平方．当且仅当ad=bc时等号成立．a,b,c,d可以是任意的实数．

问题6学习了柯西不等式有什么用处?

生13:可以在证明一些不等式的过程中运用该结论．

生14:由刚刚求得的平行四边形面积和证明函数f(x)≥0的过程,我们可以解决一些最值问题．

师:很好．我们来看看以下几题．

例题已知a2+b2=1,c2+d2=5,求ac+bd的最大值．

变式1已知a2+b2=1,求证:|acosθ+bsinθ|≤1．

变式2已知a2+b2=1,求a+2b的最大值．

(先让学生思考,教师可根据实际情况,引导学生对变式1和变式2中的柯西不等式进行变形,让学生理解后再独立完成,再练习类似的题目加以巩固.)

师:变式1中出现了绝对值,似乎不符合柯西不等式的形式,如何变形出现平方项?(加平方后出现平方项,|acosθ+bsinθ|2≤(a2+b2)(cos2θ+sin2θ),满足柯西不等式的形式.)

师:变式2中如何出现积的和的平方?(进行拆分构造,出现4项,满足柯西不等式的表达形式(a+2b)2=(1·a+2·b)2≤(12+22)(a2+b2))．

设计意图三个题目由易到难具有一定的梯度,学生在自主探究的过程中,加深了对柯西不等式结构上的认识,形成解题技能．突出等号成立的条件又可以强调解题的规范性,提高了学生推理论证的能力．此过程帮助学生对柯西不等式进行建构,达到对象阶段的要求．

第四阶段形成阶段(图式阶段)——辨析与反思

师:柯西不等式的应用范围广泛,但不易识记,我们通过柯西不等式的一个变式,从它的结构特征来欣赏它．

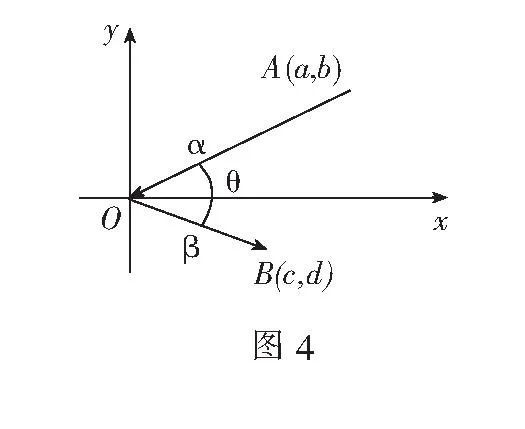
生15:左边像是表示(a,b),(c,d)两点到原点之间的距离之积．

生16:右边就表示(a,b),(c,d)两向量的数量积．我又发现,要是记α=(a,b),β=(c,d),那就有|α||β|≥|α||β|cos(π-θ)=α·β,这个是肯定成立的．

生17:原来我们也可以这样去证明柯西不等式．给两边加平方就是柯西不等式了．

师:很好．但这里要注意,因为是表示三角形的边长,默认a,b,c,d均大于0,但柯西不等式是强调对一切实数都成立,所以有

师:这样，柯西不等式也可以用几何的形式来表示了．如何用文字去表述?

生18:模长之积大于或等于数量积．

师:很好,从这个图象我们也就能更加清楚理解柯西不等式．

师:向量形式是柯西不等式的另一种表述形式．有关柯西不等式的向量表达形式及性质,我们将放在下一节课讲解．

评注从形的角度来看,柯西不等式具有特定的几何意义；从数的角度来看,柯西不等式揭示了“和”与“积”这两种结构间的不等关系．

设计意图通过图形的认识,培养学生数形结合的思想,加强学生多方面思考问题的能力．完成最后图式阶段,使学生从数和形两方面掌握完整的柯西不等式的内涵,并能在解决问题时创设与知识相关的问题情境．

上述案例,按照这一理念,围绕着“活动”、“过程”、“对象”和“图式”四个阶段实施教学,环环相扣,循序渐进,牵引并支持着学生在自己的经验和数学本质之间不断对话．在连续性地回顾与反思过程中提升、扩充学生的经验与认识,深化对柯西不等式本质的理解,使学生明确了:

(1) 柯西不等式的推导过程及教学背景;

(2) 柯西不等式中有哪些规定和限制条件,它们与以前学过的哪些知识有着怎样的联系;

(3) 柯西不等式的表达形式及其特点;

(4) 柯西不等式的等价叙述;

(5) 运用柯西不等式能够解决哪些数学问题．

从而实现了真正意义上的柯西不等式知识建构,帮助学生从本质上理解了柯西不等式．但运用APOS 理论指导柯西不等式教学时需要注意以下几点．

(1) 数学知识的建构应遵循循序渐进的原则,不能一蹴而就．这就需要经过多次反复,循序渐进,螺旋上升,直至学生真正理解．柯西不等式的向量形式较难,考虑到学生的实际接受情况,笔者将以本节课的知识作为铺垫,把向量形式的柯西不等式放在下一节课讲解．这正是体现了循序渐进,螺旋上升的原则．

(2) 不能将APOS 绝对化,实际操作时,往往“活动”与“思考”可以穿插进行,活动中有思考,思考中有活动．“对象”与“图式”也可以穿插进行,两个阶段可以交替螺旋式进行．在本教学案例中,“活动”与“思考”总是相伴相随．在活动阶段中的“赵爽弦图”也含有“图式”成分．教师要以实现学生知识建构为目的,根据实际,灵活运用,提升教学效果．

尽管APOS理论为我们提供了柯西不等式的教学模式,但在教学实践中我们仍需要不断反思,不断改进．只有在师生共同的努力下,才能从根本上完成柯西不等式的知识建构,帮助学生从本质上理解柯西不等式．

○学习指导○