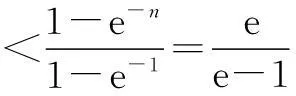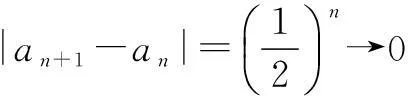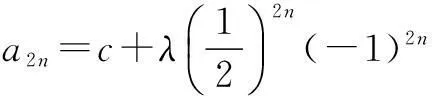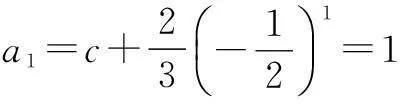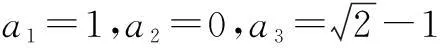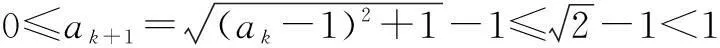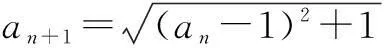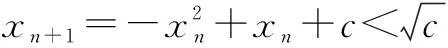用极限思想解决数列问题



用极限思想解决数列问题

杨俊

(安徽省舒城中学，231300)

极限的思想是近代数学的重要思想.极限思想在解决中学数学中变量间的无穷运动问题时,可以帮助我们直观理解问题的最终形态,特别是针对近几年的各地高考题所设置的高等数学背景下的中等数学问题,有很好的使用效果,能大大提升解决问题的概率．

一、用极限的思想解决数列的求和问题

在不等式中解决代数式与常数大小证明问题时,如利用极限思想构造一个以该常数为极限的加强不等式,往往可使问题得以轻松解决．

例1求证:

证明因为n→+∞时,

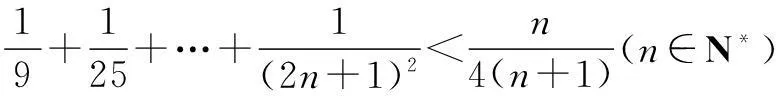
假设当n=k(≥1)时成立,即

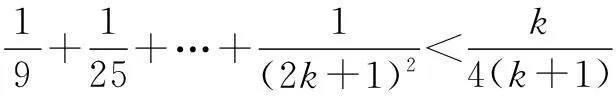
则当n=k+1时

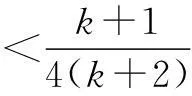
所以,当n=k+1时命题成立.

评注该题直接用数学归纳法很难处理,但将不等式右式通过极限的思想构造一个关于n的代数式,就把问题转化为用数学归纳法处理问题的常见题型,使问题很容易得以解决．

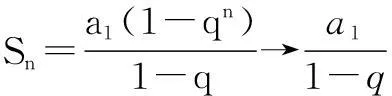
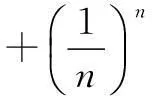
二、利用极限的思想求解数列的通项公式

在下面的问题中用极限思想解决,能够让我们站在更高的角度看待问题,使问题结构更清晰,方向更明确,解决问题的思路更有条理性．

例3(2014年湖南高考题)已知数列{an}满足a1=1,|an+1-an|=pn，n∈N*

(1)若数列{an}是递增数列,且a1,2a2,3a3成等差数列,求p的值;

解(1)略.

由于{a2n-1}是递增数列,{a2n}是递减数列,所以存在常数c,使得

n→+∞时,a2n-1→c,a2n→c且

(*)

(** )

三、利用极限思想求数列中的参数范围

在数列中求参数范围问题,对参数范围的估计是构建问题解决方案的一大难点,不能估计出参数的范围,解题的方向性就不够明确．所以若能够用极限的思想先估算出参数范围,则只需对估算的结果做出证明即可,往往能收到奇效．

例4(2014年重庆高考题)设a1=1,

(1)若b=1,求a2,a3及数列{an}的通项公式;

(2)若b=-1,问:是否存在实数c使得a2n

解(1)略.

(2)(i)先用数学归纳法证明:对n∈N*，有0≤an≤1.

综上，0≤an≤1. 特别地,n≥3时，0

(ii)其次证明{a2n-1}是递减数列,{a2n}是递增数列.

事实上

a2k+3-a2k+1

由于

>0,a2k+2+a2k-2<0，

所以a2k+3-a2k+1与a2k+2-a2k异号.

(*)

以下用数学归纳法证明(*)成立：

(1)证明:数列{xn}为递增数列的充要条件是c<0;

(2)求c的取值范围,使数列{xn}为递增数列.

解(1)略.

(*)

评注数列中求参数范围多年来都是高考中的难点问题,因为这种题型高度抽象与概括,变形灵活,构思巧妙,这给学生答题造成了很大难度.运用极限思想,可使参数取值范围明确化,解决问题的方向和策略更清晰．