基于Multisim的一个三阶动力系统的电路实现*

尹社会，皮小力（河南工业职业技术学院，473000，河南，南阳）

基于Multisim的一个三阶动力系统的电路实现*

尹社会†，皮小力
（河南工业职业技术学院，473000，河南，南阳）

利用Matlab软件和理论分析，对新构建的一个新三阶动力系统进行了研究和分析，得到了该动力系统在一定参数组合和初值下的Lyapunov指数和Lyapunov维数，也探讨了其电路的实现可能性，并利用Multisim软件搭建了基本模拟电路，结果表示新动力系统不同于现有的三维混沌系统，具有丰富的动力学行为，也验证了其物理可实现性。

动力系统；Lyapunov指数；动力学行为；Multisim软件；模拟电路

1 引言

混沌理论的发展日新月异，著名的Lorenz系统族成为混沌系统理论研究的典型，以Lorenz系统[1]为基础构造了大量的新混沌系统和新超混沌系统，除了以混沌反控制方法构造的Chen系统[2]、Lü系统[3]和统一混沌系统[4]以外，还有很多类似的新混沌系统，比如T系统[5]、Liu系统[6]、Bao系统[7]、Qi系统[8]、Yang-Chen系统[9]等，新系统的提出促进了人们对混沌现象的深入研究和认识，提高了混沌理论在工程上的应用能力。关于混沌系统的复杂动力学行为的判定以及混沌控制和同步研究一直是研究的热门课题[10-12]。本文根据新混沌系统的必要条件和混沌系统的验证方法，通过数学分析和数值计算不仅给出了平衡点类型还给出了新混沌系统对应的奇怪吸引子相图、Lyapunov指数、平衡点稳定性分析等结论。然后结合电路模拟软件Multisim搭建了模块化电路，结果和数值计算相一致。

2 数学模型及基本性质

构造的三维自治动力系统的方程为[13]：

其中：（x, y,z）∈ R3为状态变量，a,b,c,d为系统实参数。当 a =8,b =0.05,c=2,d=4时，其初值取(0.01,0.01,0.01)，系统（1）的吸引子轨线的相图如图1所示。

由数值计算可得系统的3个Lyapunov指数分别为：λ1=0.362,λ2=0,=-2.323,其中有1个Lyapunov指数大于0，1个Lyapunov指数等于0，1个Lyapunov指数小于0，且3个Lyapunov指数之和小于0，Lyapunov维数可以计算出 DL=2.16，这说明系统在上述参数组合下处于混沌状态。

3 系统的平衡点分析

图1 系统吸引子相图

4 系统的电路实现

为了验证系统（1）的混沌特性，利用电子电路模拟软件Multisim的仿真功能，运用模块化的思想在该平台上构建设计了一个模拟自激振荡电路，如图2所示。该电路由模块化的积分器、反相加法器、反相器和乘法器构成，这些模块可以分别实现系统中的求导、加减、负号和乘积运算。该自激振荡电路所采用的集成运算放大器的型号为LM324，采用的乘法器为AD633，为了保证集成运算放大器正常工作，需要将电源电压限定为［-1 2 V,12V］之间。由于原微分方程的解的界超出这一范围，所以需要进行相应的变量比例压缩变换，为可靠起见，即将变量 x ,z进行比例压缩系数为的压缩操作。

为方便确定电路中的具体参数，下面列出电路的状态方程：

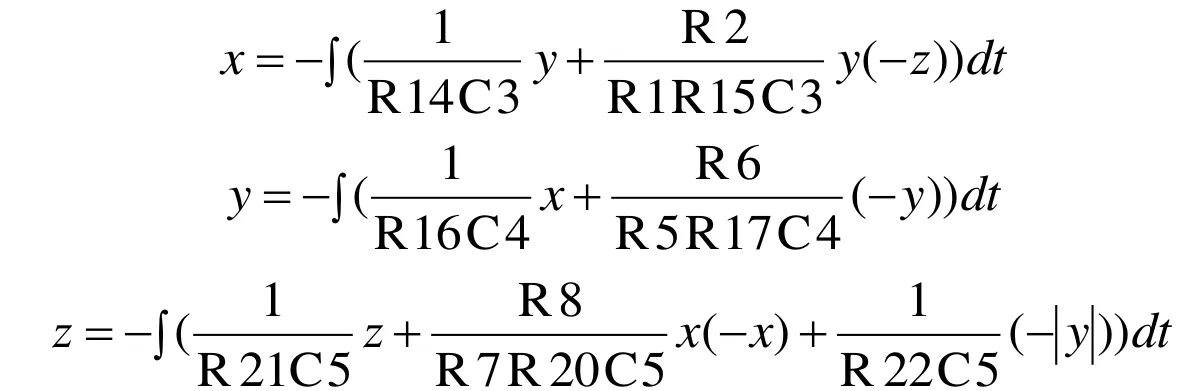
其中- y 的实现靠 - y⋅sign(y)，符号函数 s ign( ⋅)通过运算放大器的饱和来实现，由于LM324在双电源VCC和VEE作用下，饱和电压为 ± 1 6V，因此可以通过结合反相比例电路实现符号函数功能。为了方便，不妨取电路元件参数为 R 1 =R 2=R5=R6=10kΩ， R 7 =R 8=R9=R10=R16=R20=10kΩ， R 3=1 kΩ，R4=1 6kΩ， R 1 4=1 25kΩ， R 1 5=1 00kΩ， R 1 7=2 000kΩ， R 2 1=5 0kΩ， R 2 2=2 50kΩ。通过反复调节元件参数，电容取值为 C 3 =C 4=C5=1μF。

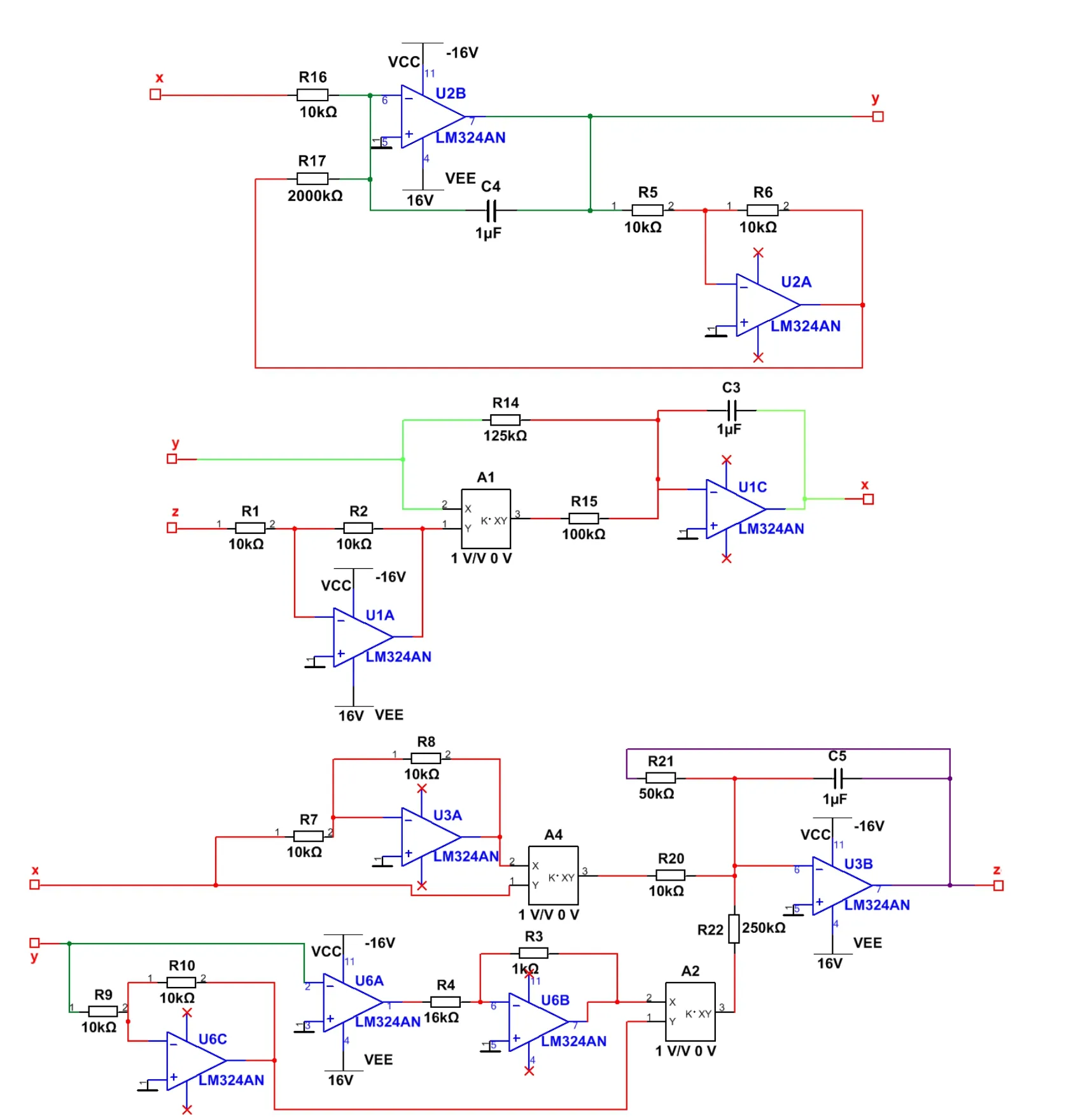
图2 电路原理图

在系统参数 a =8, b=0.05,c =2,d=4的情况下，模拟电路的示波器波形图如图3所示，示波器相图如图4所示，结果与数值仿真（图1）比较基本一致，说明搭建的电路符合混沌系统要求，同时也验证了系统的物理可实现性。

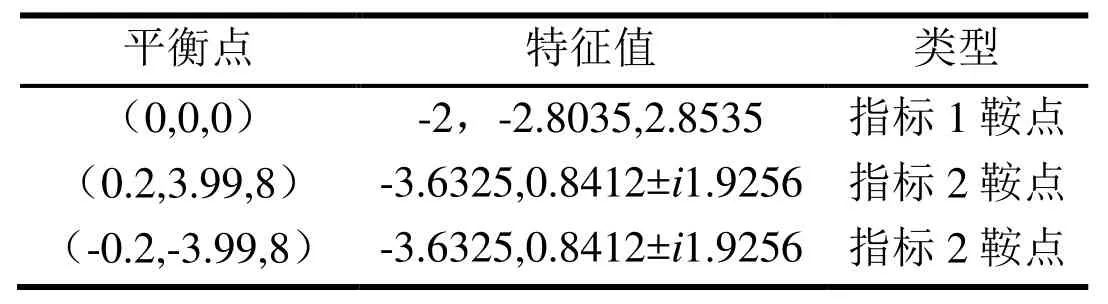
表1 系统(2)的平衡点及特征值

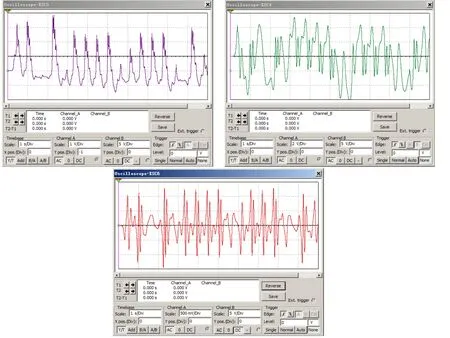
图3 示波器显示状态波形图

图4 示波器显示相图

4 结论

本文研究了一种三维自治动力系统及对应的分数阶混沌系统，给出了整数阶动力系统的吸引子相图、Lyapunov指数和Lyapunov维数等基本动力学特性。基于稳定性理论和数值计算对系统平衡点进行了分析，利用Multisim软件实现了模块化模拟电路，结果显示与数值仿真相一致，充分说明了系统的物理可实现性。这些结论为系统的模拟电子电路的实现和通信工程等应用提供了理论依据和参考。

[1] Lorenz E N. Deterministic non-periods flows[J]. Journal of Atmosphere Science, 1963, 20(2):130-141.

[2] Guan-rong CHEN, Tetsushi UETA. Yet another chaotic attractor[J]. International Journal of Bifurcation and Chaos, 1999, 9(7): 1465-1466.

[3] Jin-hu Lü, Guan-rong Chen. A new chaotic attractor coined[J]. International Journal of Bifurcation and Chaos, 2002, 12(3): 659-661.

[4] Jin-hu Lü, Guan-rong Chen, Dai-zhan CHENG, et al. Bridge the gap between the Lorenz system and the Chen system[J]. International Journal of Bifurcation and Chaos, 2002, 12(12): 2917-2926.

[5] G H TIGAN. Analysis of a dynamical system derived from the Lorenz system[J]. Sci Bull Poli-tehnica University of Timisoara, 2005, 50(64): 61-72.

[6] Chong-xin Liu, Tao Liu, Ling Liu, Kai Liu. A new chaotic attractor Chaos[J]. Chaos, Solitons and Fractals, 2004; 22: 1031-1038.

[7] BAO Bocheng, LIU Zhong, XU Jianping. New chaotic system and its hyperchaos generation[J]. Journal of systems engineering and electrics, 2009, 20(6): 1179-1187.

[8] QI Guoyuan, CHEN Guanrong, DU Shengzhi, et al. Analysis of a new chaotic system[J]. Physica A, 2005, 352(2-4): 295-308.

[9] YANG Qi-gui, CHEN Guan-rong. A chaotic system with one saddle and two stable node-foci[J]. International Journal of Bifurcation and chaos, 2008, 18(5): 1393-1414.

[10] 尹社会，张勇，张付臣, 等. 基于Lorenz系统的强迫Lorenz混沌系统的动力学研究[J].东北师大学报(自然科学版), 2014, 46(1): 42-47.

[11] 陈红, 周攀. 一个四维系统的混沌动力学分析[J]. 甘肃科学学报, 2013, 25(1): 13-16.

[12] 尹社会, 李德雪, 张勇. 新三维非线性系统的全局动力学研究[J]. 甘肃科学学报, 2015, 27(4): 87-90.

[13] 尹社会, 张勇, 舒永录. 一个新三阶动力系统及其仿真[J]. 通化师范学院学报(自然科学版), 2015, 36(5): 22-24.

O415.5

：A

1003-7551(2016)01-0029-05

2016-01-10

南阳市科技发展计划项目(2012GG035; 2013RK013)

† 通讯作者： hnzkny@126.com