单模行波激光系统及其电路设计

唐 珩，农丽萍，阳 丽( . 广西桂林市第十八中学，广西 桂林 54004; . 广西师范大学物理科学与技术学院，广西桂林 54004)

单模行波激光系统及其电路设计

唐 珩1，农丽萍2†，阳 丽2
( 1. 广西桂林市第十八中学，广西 桂林 541004; 2. 广西师范大学物理科学与技术学院，广西桂林 541004)

对无失谐的单模行波激光系统进行了数值仿真研究，该系统在特定参数下具有丰富的动力学行为，同时对该系统进行了电路仿真设计。

激光系统；混沌；电路

1 单模行波激光系统动力学特性

光学混沌[1-3]是混沌研究的一个分支，随着非线性科学的发展，光学混沌也取得了长足进展。在激光器[4-5]中观察到混沌现也已不足为奇，这表明了激光器系统具有丰富的动力学行为。位了研究其动力学行为，我们利用文献[6]给出的无失谐单模行波激光系统微分方程组形式，具体形式为（1）式：

图1 系统变量E、P、D的时域图

现在我们考察一下，当参数 R发生变化的时候，系统变量随着 R变化的情况，如图 3所示。这里β=2 ,σ =0 .9。从分岔图可以看出单模行波激光系统随着R的变化，当25 ≤ R ≤ 3 6.78时，单模行波激光系统的3个变量表现为周期1的运动，当36.79 ≤ R ≤ 5 0时，单模行波激光系统进入混沌状态。

当系统参数 β =2 ,σ =0 .9,R=1 5时，单模行波激光系统吸引子表现为不动点，如图4所示；当β=2 ,σ=0 .9,R=3 6.78时，单模行波激光系统吸引子表现为极限环，如图5所示。

图2 系统混沌吸引子在EP平面、ED平面、PD平面上的投影

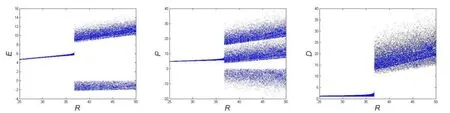
图3 系统变量E、P、D分岔图

进一步，考察单模激光系统的散度：

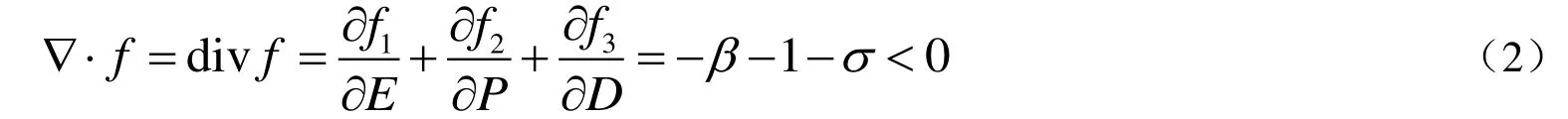
显然，单模行波激光系统的散度小于 0，这是一个耗散系统，体积要收缩到零。这种体积收缩作用将使相轨迹必须折回来，即产生折叠运动。拉伸运动和折叠运动两者相互作用的结果，只能是形成具有分形和分维的混沌运动。当系统参数时，单模行波激光系统发生霍普分岔，系统混沌吸引子三维相图如图6所示。

2 单模行波激光系统的改进型电路设计

考虑到上述系统的变量已经超出运算放大器的线性动态范围±13.5V，故首先对单模行波激光系统变量做比例压缩变换，然后设其中k为变量比例压缩因子。设 0.5 k= ，得变换后的方程为

接下来，对上式作微分-积分转换，得到标准化处理后的状态方程为

根据（4）式得到对应的模块化电路设计结果如图7所示。EWB仿真后的结果如图8所示，仿真结果表明单模行波激光系统具有丰富的动力学行为。

图4 吸引子为不动点

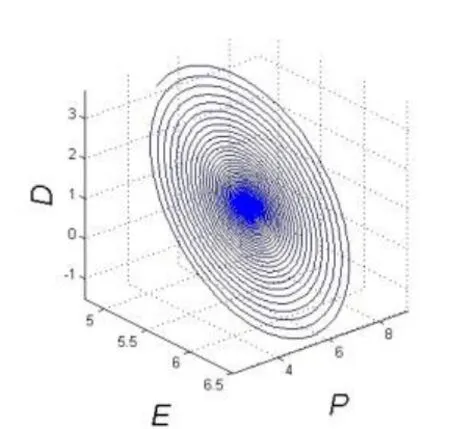
图5 吸引子为极限环

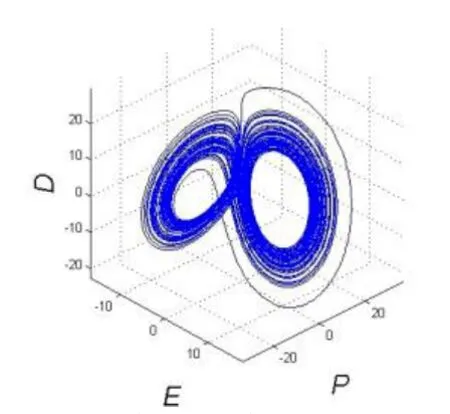
图6 混沌吸引子

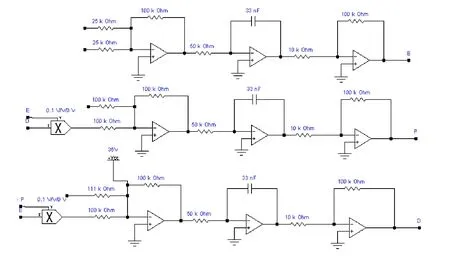
图7 单模行波激光系统的模块化电路设计结果

图8 作比例压缩后系统混沌吸引子相图

3 结论

本文对无失谐单模行波激光系统的混沌特性进行了分析，计算出在给定参数情况下系统出现混沌现象、周期现象，并通过电路进行了仿真，证实了该系统的确存在着十分丰富的动力学行为。

[1] L Pesquera, F J Bermejo. Dynamics of Non-Linear Optical Systems[M]. Singapore: World Scientific, 1989.

[2] N B Abraham, F T Arecchi, L A Lugiato. Instabilities and Chaos in Quantum Opics[M]. New York: Plenum Press, 1988.

[3] 张洪钧. 光学混沌[M]. 上海：上海科技教育出版社，1997.

[4] 张纪岳. 三维模型下单模行波激光的不稳定性[J]. 西北大学学报, 198, 2(16): 14-20.

[5] 张纪岳. 四维模型下模行波激光的不稳定性[J]. 中国激光, 1986, 9: 515-516.

[6] 张纪岳. 单模行波激光系统混沌行为的Lyapunov指数分析[J]. 西北建筑工程学院学报, 1996, 3: 6-11.

TN241

A

1003-7551(2016)01-0022-03

2016-01-22

国家自然科学基金项目(61307096,61565002)；广西自然科学基金项目(2013GXNSFBA019006, 2014GXNSFBA118282)；广西教育厅项目（2013YB033；D20140213）；2015年广西师范大学教育教学改革项目；广西高等教育本科教学改革工程项目（2015JGA282）

† 通讯作者：lovenlp@qq.com