应用电各向异性介质电多极展开计算电势

李文略(岭南师范学院基础教育学院，广东 湛江 524037)

应用电各向异性介质电多极展开计算电势

李文略†
(岭南师范学院基础教育学院，广东 湛江 524037)

应用张量分析的矩阵方法得到电各向介质中多极展开式在主轴坐标系下的具体形式。应用该具体形式结合广义坐标变换法计算均匀带电圆盘、椭圆盘、椭圆环、圆环和旋转椭球在电各向异性介质中远场的电势，所得的结果在ε22=ε33=ε的情况下，可过渡到在电各向同性介质中远场的电势。

电各向异性介质；电势；电多极展开；张量；椭圆盘；旋转椭球

1 引言

电各向同性介质静电场的求解方法很多，如分离变量法、电像法、格林函数法、电多极展开法等等。陈燊年[1]等系统的研究了电各向异性介质（限于有且只有三个正交主轴方向的电介质）的静电场，其中有应用分离变量法和电多极展开法有效的求解了电各向异性介质中的静电场。李洲圣，唐长红[2]系统的定义了张量分析的矩阵方法，文[3-4]应用该方法研究了电（磁）各向异性介质的电磁场。本文将在前人研究[1、5]的基础上，应用张量分析的矩阵方法推导得到电多极展开式在主轴坐标系下的具体形式，进而应用该具体形式结合广义坐标变换法计算电各向异性介质中均匀带电圆盘、圆环、椭圆盘、椭圆环和旋转椭球等典型的连续带电体在远场处激发的电势，可作为应用电多极展开式计算电势的补充。

2 各向异性介质中电多极展开式的具体形式

在电各向异性介质中在主轴坐标系321xO- 下，坐标原点建在源区，当电荷系统分布在小区域内，在远处产生的电势多极展开式为[1、5]

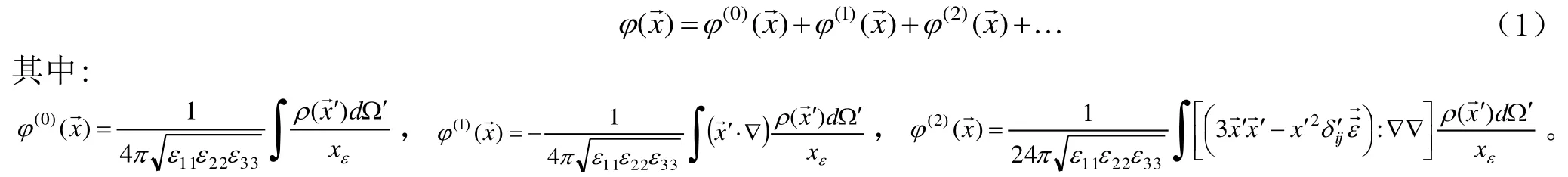
式中: x→、x′→分别表示场点和源点的位矢)(x′→ρ、Ωd 分别表示源电荷密度和源电荷体积元；)0(φ、)1(φ 和)2(φ分别称为电零极项、电偶极项和电四极项；，11ε 、22ε、33ε为沿着主轴坐标系中:

设电各向异性介质的主轴坐标系O-x1x2x3，记为的转置形态，它们均表示同一坐标系。现应用张量分析的矩阵方法计算φ(1)（x）和φ(2)（x）在主轴坐标系下的具体形式。三个坐标轴正方向的介电常数。在实际中用得较多的通常只到)2(φ，因而本文涉及的计算也到)2(φ 为止。)2(φ 项

将式（2）（3）代入式（1）中，由多元函数二阶偏导数及链式法则，可得

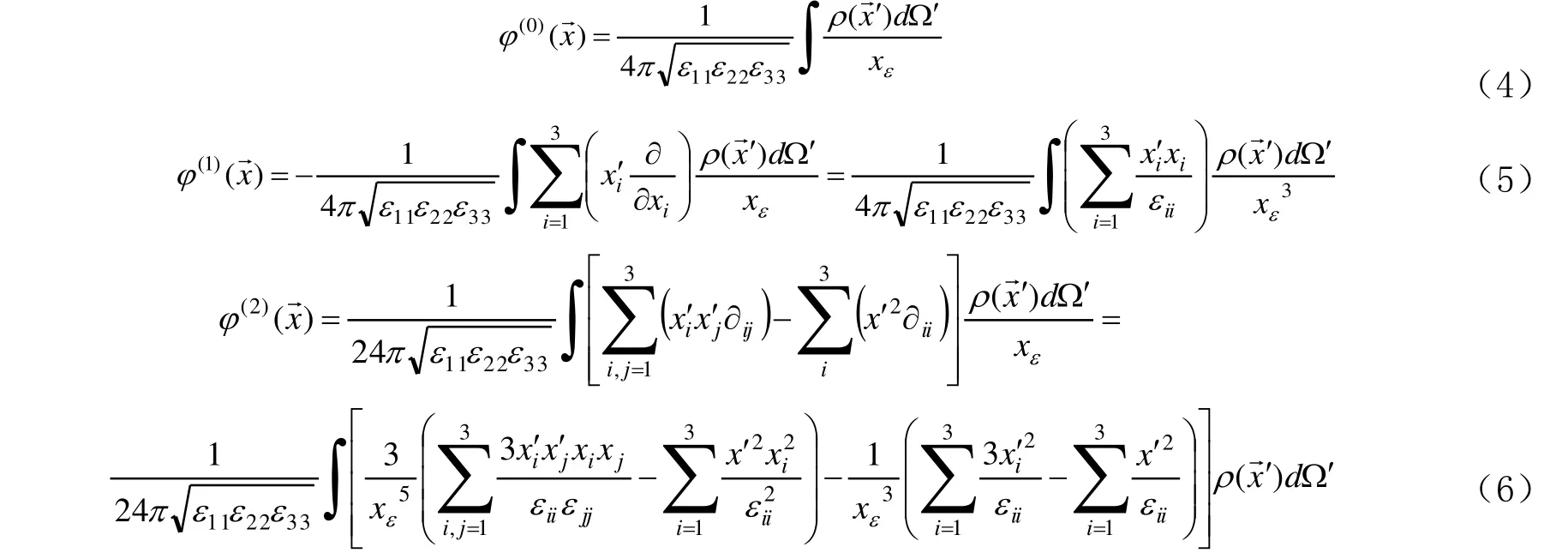
式（4）（5）（6）即为电各向异性介质中电多极展开在主轴坐标系下的具体形式。若令ε22=ε33=ε代入式（4）（5）（6）中，则可得到电各向同性介质中电多极展开的具体形式。应用具体形式结合广义坐标变换法可直接方便的计算连续带电体系在远场处的电势，而无需求解电偶极矩或电四极矩以及进行张量的多重点积运算.以下应用该具体形式直接计算典型连续带电体远场处的电势。

3 电各向异性介质中均匀带电圆盘、圆环远场处的电势

均匀带电面密度为σ，电量为Q，半径为R圆盘放置在主轴坐标系 O-x1x2x3（原点在圆盘中心）的 O -x1x2面上，应用具体形式求其在远场点 P()处的电势。

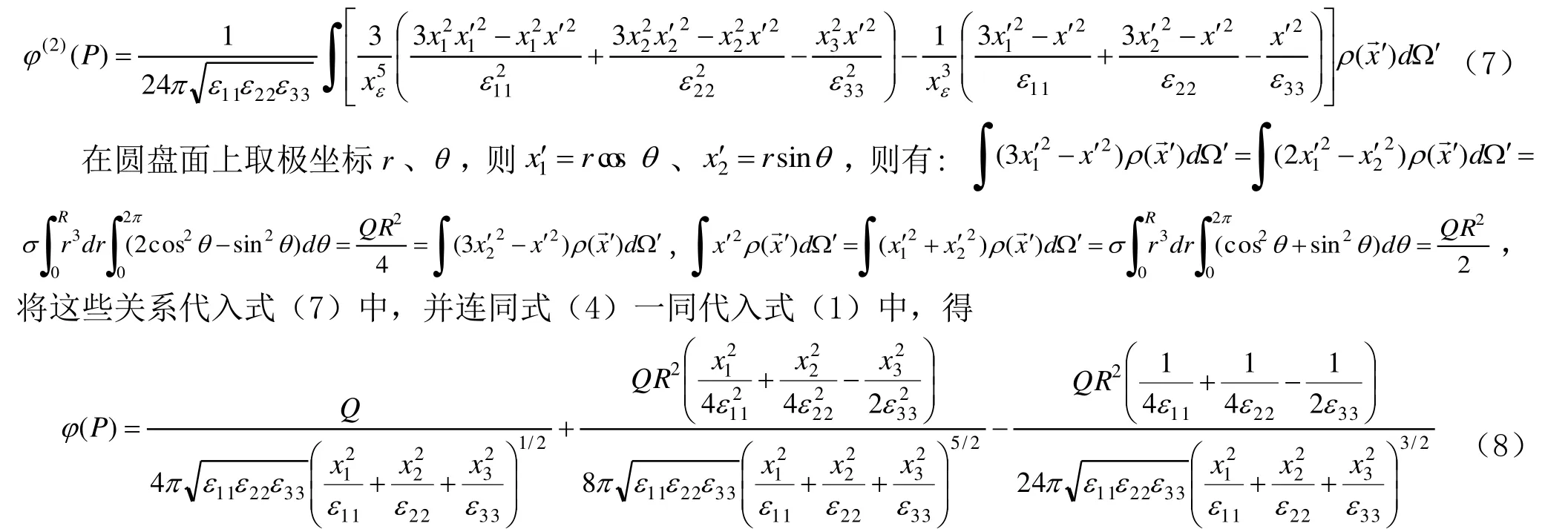
若此圆盘变为半径为R的圆环，带电线密度为λ，电量为Q，取极坐标r、θ，则 x1′ =Rcosθ、x ′2=R sinθ，

4 电各向异性介质中均匀带电椭圆盘、椭圆环远场处的电势

4.1 均匀带电椭圆盘远场处的电势

均匀带电面密度为σ，电量为Q，长、短半轴为a、b的椭圆盘放置在主轴坐标系321xxxO- （原点在椭圆盘中心，长半轴沿着1x轴）的21xxO- 面上，应用具体形式求其在远场点),,(321xxxP 处的电势。

若令 Rba == （椭圆盘变为半径为R的圆盘），代入式（11）中可得圆盘在远场激发的电势，结果与式（8）一致，藉此可验证用多极展开具体形式计算远场电势的正确性.

4.2 均匀带电椭圆环远场处的电势

带电线密度为λ，电量为Q，长、短半轴为a、b的椭圆环，放置在主轴坐标系321xxxO- （原点在椭圆环中心，长半轴沿着1x轴）的21xxO- 面上，应用具体形式求其在远场点 ),,(321xxxP 处的电势.在环面上取广

若令 Rba == 代入式（12）中，即可得均匀带电圆环在远场的电势，如果与式（9）相同.

5 电各向异性介质中均匀带电旋转椭球远场处的电势

均匀带电密度为ρ，电量为Q，长、短半轴为a、b的椭球，主轴坐标系 O - x1x2x3的原点在球心，长半轴沿着x3轴，应用电多极展开的具体形式求其在远场点 P ( x1, x2,x3)处的电势。

椭球电荷分布关于x1轴、 x2轴和 x3轴对称，故(P)=0，且由式（6）得

6 结语

文[1、5]应用电多极展开式计算电各向异性介质的静电场时，需先求出电多极矩，然后再进行（矢量）张量间的多重点积运算。本文应用电多极展开式的具体形式结合广义坐标变换法可方便的计算均匀带电圆盘、圆环、椭圆盘、椭圆环和旋转椭球在远场处电势，计算的过程充分的利用电荷对称分布的条件简化了计算，也避免了求电多极矩、进行（矢量）张量间的多重点积和涉及椭圆积分的繁琐运算，可作为现有应用电多极展开求解电各向异性介质中静电场的补充。在令ε22=ε33=ε的情况下，所得的结果适用于电各向同性介质中的静电场。

[1] 陈燊年, 洪清泉, 王建成.介质为各向异性的电磁场[M]. 北京: 科学出版社, 2012.

[2] 李洲圣, 唐长红. 三维空间张量分析的矩阵方法[M]. 北京: 航空工业出版社, 2010.

[3] 李文略. 各向异性磁介质中ζ空间与χ空间的变换关系及应用[J]. 广西物理, 2015, 36(2): 20-23.

[4] 李文略. 电各向异性介质中泊松方程的具体形式[J]. 泉州师范学院学报, 2015, 33(2): 93-96.

[5] 郭震宁, 陈燊年. 在各向异性介质中电势的多极矩展开[J]. 华侨大学学报(自然科学版), 1993, 14(4): 440-446.

[6] 袁德荣. 球张量的多极展开法[J]. 湖北大学学报(自然科学版), 1988, (1): 94-98.

O441.1

A

1003-7551(2016)01-0025-04

2015-12-20

†通讯作者：physics2009ed@126.com