晶体相场法模拟微裂纹的扩展行为*

叶 里，黄礼琳，宁岁婷，满 海，高英俊（广西大学物理科学与工程技术学院 广西南宁 530004）

晶体相场法模拟微裂纹的扩展行为*

叶 里，黄礼琳，宁岁婷，满 海，高英俊†
（广西大学物理科学与工程技术学院 广西南宁 530004）

用晶体相场模型模拟预变形条件下的单轴拉伸的裂纹扩展行为. 展示出裂纹扩展过程的演化图。从裂纹演化图可以清楚的观察到，随着应变量的增加，裂纹长度增加，裂纹呈钝化-扩展-钝化的扩展模式，裂纹形状为锯齿形；随着预变形量的增加，解理方式的裂纹扩展减弱, 转变成锯齿形状的裂纹扩展方式。

微裂纹；晶体相场；模拟实验

1 引言

材料的变形与破坏大都源自材料的微结构，如空位、位错、晶界与微裂纹等。要想深入研究材料的变形与破坏的特性与机理，还需要开展多尺度分析，把宏观分析与微纳观分析结合起来，在更深的层次上找到问题的根源和变形破坏机制[1]。现在，对金属材料裂纹扩展的研究，早已不再局限于宏观和介观层次，而是已经逐渐地深入到微纳观层次。由于纳米级微裂纹形核与扩展，在金属材料微观缺陷中普遍存在，它严重地降低了构件的使用寿命[2]，因此，研究纳米级裂纹的萌生和扩展对预防材料的断裂，提高构件的使用寿命具有重要意义[3]。在当前的实验测量条件下，对材料的纳米级裂纹扩展很难实时观测[4]，因此，发挥计算模拟实验的优势，应用其研究微纳米尺度的微裂纹就显得极为迫切和重要[5-8]。近几年，基于密度泛函理论建立的晶体相场方法(PFC)[9]，通过引入周期性原子密度函数，用以描述晶体点阵结构，能够自洽地耦合了弹性效应等周期性结构的物理特性…PFC方法能很好地用于描述晶界和位错在扩散时间尺度下的运动特征[10]，并用于模拟纳米级的裂纹扩展行为和演化过程[11-13]。本文应用PFC方法研究预变形条件下，单轴拉伸应变的裂纹生长特征和扩展规律，揭示纳米级裂纹扩展对材料断裂的作用。

2 PFC模型与方法

2.1 PFC模型

PFC模型能够揭示晶体学结构特性以及空间尺度为原子尺度，时间尺度为扩散时间尺度下的行为。对于固态金属材料，其原子的位置呈规则周期性排列，通过引入周期性相场变量，其局域位置的最大值对应于原子的位置；对于均匀相（液相等）中的原子分布为均值分布，其值为常量。用周期原子密度函数作为相场变量，符合上述两方面的要求。其表达式可以写成[10-12]

式中，等号右边第1项反映的是晶格原子的周期排列结构特征，第2项反映的是均匀相（如液相）等的原子分布，其均值为常量。此时，系统无量纲的自由能函数可以写成[12]

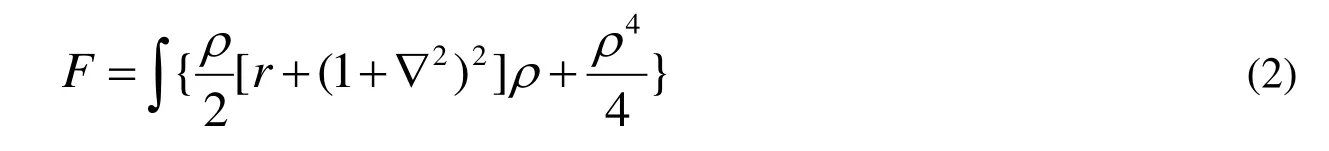
式中，为局域原子密度；为与温度有关的唯象参数；为拉普拉斯算子。在单模近似下，可以求得式子(2)的一个稳定特解为

2.2 动力学方程

本文采用保守场Cahn-Hilliard动力学方程[10-12]描述原子密度随时间的演化。该方程具体如下方程表示：

式中，ρ为原子密度，r表征体系的过冷度，∇为拉普拉斯算子，t为时间变量。

图1 单模近似得出的二维相图(阴影部分代表两相共存区)[9]

2.3 数值计算方法

对无量纲动力学演化方程(4)采用半隐式傅里叶伪谱方法[10-12]求解，其离散形式为

2.4 样品制备与应变施加

为方便起见，本文选取二维薄膜体系来模拟裂纹扩展。固相基体用三角相点阵表示，选取晶体原子密度参数为 ρ0=0.49，温度参数 r =-1.0（图1中B点）。对单晶样品的微裂纹扩展进行模拟时，计算模拟区域为1024 x 512y，单位格子长度x= y=…原子点阵排列方向与y轴夹角为3.5°。在样品的中心位置，设置半径 r =8格子的圆形缺口作为初始裂口，缺口处的热力学参数设置为 ρ0=0.79，温度参数 r=-1.0，如图1中A点所示。由于不涉及材料的物性参数，对模拟所用的参数进行无量纲化处理，并将连续空间离散为正方格子分布…计算时四周边界采用周期性边界条件。

采用式(3)设置一个含有圆形裂口的区域，经过弛豫5步，得到具有稳定缺口样品，如图2(a)。对样品分别沿x轴和y轴施加拉伸预变形，变形量分别为ηx和ηy。经弛豫后，再在y轴方向施加拉应变，如图2(b)所示。在变形过程中，x方向空间步长保持不变，y方向空间步长随着应变速率在每一时间步长下都有一增量d =，其中，为无量纲的应变速率，n为施加拉应变的时间步长数，t为时间步长。

图2 (a) 具有初始裂口样品，图2(b) 沿y轴方向施加拉应变的示意图

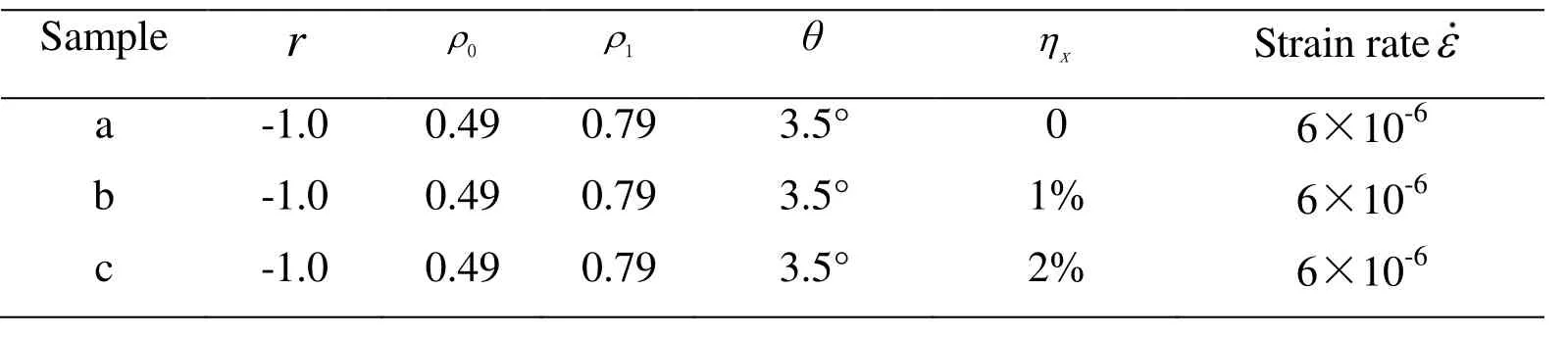
表1 样品的热力学参数和预变形量

3 结果与分析

3.1 沿x方向拉伸预变形样品的裂纹扩展

由图 3(a1)可以看到，对于没有预拉伸作用的裂口样品a，在拉伸的初始阶段，当应变量未达到裂纹扩展的临界应变之时，预制裂口没有出现明显的变化。当应变量达到0.138时，样品中部圆形裂口开始起裂，在裂口左右两边边缘处，出现约2个原子尺度的微裂纹。随着应变量的不断增大，裂纹尖端出现钝化过程，直至裂纹尖端集中的应力，超过某个方向上的原子结合力，导致该原子键断裂，从而驱动裂纹开始扩展，如图3(a2)。此时，裂纹的开裂方向与拉应变方向垂直，拉应变是y轴方向，裂纹的开裂方向为x轴方向。当外加应变量达到0.186时，裂纹开裂长度约为样品x方向长度的1/3，如图3(a3)所示。在开裂过程中，裂纹生长呈现扩展-钝化-扩展的长大特征[14]。这一长大特征，可以看成是裂纹扩展通过主次原子排列方向的原子键交替断裂而进行裂尖扩展，裂纹边缘呈锯齿形，如图3(a4)放大图所示。这与文献[20]相互印证。随着应变量的不断增加，裂纹继续扩展，当应变量达到0.210时，观察图3(a4)，可以看到此时裂纹长度约占模拟试样x轴总长度的 4/5，此时，试样即将被拉断。在裂纹扩展模拟的后期，应力的作用直接导致某固定原子排列方向的原子键断裂，出现微裂纹尖端的解理断裂扩展。解理裂开方向与拉伸应变方向夹角约为 60°，并以裂纹尖端中心线为轴线形成了类似孪晶的对称原子晶格排列，这与文献[14]的研究结果一致。

由图3(b1)可以看到，在x轴预拉伸量为1%，应变量达到0.138时，样品中部圆形裂口左右两边已经各有一条4至5个原子尺度的微小裂纹。观察图3(b2)，当外加应变量达到0.162的时候，从微裂纹扩展图可以看出，这时的微裂纹依旧比图3(a2)的裂纹要稍长，且此时的裂纹走向比图3(a2)要趋于水平。对于图3(b3)可以看到，当外加应变量为0.186时，裂纹呈锯齿状，且此裂纹的钝化程度要比图3(a3)的裂纹的钝化程度要高，即此裂纹比较粗。此裂纹的长度几乎与图3(a3)的相同，但图3(b3)的裂纹走向要比图3(a3)更趋向于水平，这是由于裂纹裂尖处的不同方向的原子层原子键交替断开，使得裂尖扩展方向发生转向，每次转向时扩展的裂纹长度大致相同。观察图3(b4)，此图的裂纹明显比图3(a4)的裂纹长度要短，扩展方向也更趋于水平。

图3 对应表1各组样品的裂纹模拟演化图：图a1，b1，c1的应变量为0.138；图a2，b2，c2的应变量为0.162；图a3，b3，c3的应变量为0.186；图a4，b4，c4的应变量为0.210；图a4中的放大图表示：1为主滑移系，2为次滑移系

图3(c)给出了沿x轴方向预拉伸变形量为2%的样品的裂纹扩展演化。图3(c1)给出，当拉应变量为0.138时，在中部圆形裂口左右两侧各萌生了一条微裂纹，这两条微裂纹8个原子尺度之长。图3(c2)给出，裂纹扩展方式为沿主次原子排列方向交替改变裂尖前进方向。在这裂纹扩展阶段，裂尖改变方向前进的距离几乎相等，所以此裂纹呈水平状分布。随着应变量的继续增加，当应变量增加到0.186时，观察图3(c3)，可见此裂纹明显比图3(b3)的裂纹趋于水平，且比它要粗。当应变量增加至0.210时，此时裂纹为水平状，长度约为整个模拟试样水平长度的三分之二，明显比图3(a4)和图3(b4)要短。

4 结论

本文采用晶体相场法研究施加预拉伸变形下的裂纹尖端扩展行为，结果表明：预拉伸量为0的圆形裂口在拉伸应变作用下，在拉伸应变量达到0.13左右时候开始扩展，在此时，沿x轴预拉伸变形量为1%、2%的样品，在相同的应变量下都已发生扩展，且预拉伸变形量越大，同一变形量下裂纹越长。不同预拉伸变形下的样品，在受到拉应变时，预变形量越大，起裂的临界应变越小。在裂纹扩展模拟的后期，应力的作用直接导致某固定原子排列方向的原子键断裂，出现微裂纹尖端的解理扩展。对于没有预拉伸作用的裂口样品, 解理裂开方向与拉伸应变方向夹角约为60°，并以裂纹尖端中心线为轴线形成了类似孪晶的对称原子晶格排列，这与实验研究结果一致。

[1] 邵宇飞, 王绍青. 基于准连续介质方法模拟纳米多晶体Ni中裂纹的扩展[J]. 物理学报, 2010, 10: 7258-7265.

[2] S Loehnert, C Prange, P Wriggers. Error controlled adaptive multiscale XFEM simulation of cracks[J]. Int. J. Fracture, 2012, 178:147-156.

[3] Daniele Colombo, PatrickMassinb. Fast and robust level set update for 3D non-planar X-FEM crack propagation modelling[J]. Comput. Method. Appl. M. 2011, 200: 2160-2180.

[4] M A Arafin , J A Szpunar1. A new understanding of intergranular stress corrosion cracking resistance of pipeline steel through grain boundary character and crystallographic texture studies[J]. Corros. Sci, 2009, 51:119-126.

[5] F Cadini, E Zio, D Avram. Monte Carlo-based filtering for fatigue crack growth estimation[J]. Eng. Mech, 2009, 24: 367-373.

[6] 刘晓波, 徐庆军, 刘剑. 铝裂纹扩展行为的分子动力学模拟[J]. 中国有色金属学报, 2014, 24: 1408-1413.

[7] Lei Ma, ShifangXiao, Huiqiu Deng, et al. Molecular dynamics simulation of fatigue crack propagation in bcc iron under cyclic loading[J]. International Journal of Fatigue, 2014, 68: 253-257.

[8] 刘晓骅, 邓国忠, 黄照峰, 等. 纳米晶体材料小角度晶界湮没过程研究[J]. 广西物理, 2015, 36: 1-4.

[9] K R Elder, Martin Grant. Modeling elastic and plastic deformations in nonequilibrium processing using phase field crystals[J]. Phys. Rev. E, 2004, 70: 51605-51609.

[10] J Berry, M Grant, K R Elder. Diffusive atomistic dynamics of edge dislocations in two dimensions[J]. Phys. Rev. E, 2006, 73: 609-615.

[11] 毛鸿, 罗志荣, 黄世叶, 等. 材料裂纹扩展分叉机理的晶体相场法研究[J]. 广西科学, 2015, (05): 499-505.

[12] 高英俊, 罗志荣, 邓芊芊, 等. 韧性材料的微裂纹扩展与分叉的晶体相场模拟[J]. 计算物理，2014，31: 471-484.

[13] 卢成健, 蒋丽婷, 王玉玲, 等. 晶体相场法模拟小角度晶界的位错结构及其演化[J]. 广西科学, 2013, 20(4): 316-320.

[14] 田素贵, 薛永超, 曾征, 等. 一种镍基单晶合金的中温蠕变断裂机制[J]. 稀有金属材料与工程, 2014, 43: 1092-1098.

O346.1

A

1003-7551(2016)01-0011-05

2016-01-10

国家自然科学基金项目(51161003)；广西研究生教育创新计划项目(YCSZ5015029)；广西大学生科技创新基金项目(201610593218, 201610593220)

† 通讯作者：gaoyj@gxu.edu.cn