导数视角下函数最值问题的转化求解

☉湖南省长沙市雅礼中学 刘馨忆

导数视角下函数最值问题的转化求解

☉湖南省长沙市雅礼中学 刘馨忆

近几年高考对导数方面的题主要是应用导数来解决函数问题，以导数为工具探究函数的性质，围绕函数的单调性、极值、最值展开，借此研究不等式恒成立或证明不等式等问题，着重考查分类讨论、数形结合、化归与转化等数学思想方法，进而考查我们学生的运算求解能力与推理论证能力，充分体现数学理性思维的特点，从思维的层次性、深刻性、创新性等方面进行全面考查，下面以一道导数综合问题的解答为例，探究其中所涉及的转化思想，谈谈自己的解题感悟.

一、问题展示

（1）求f（x）的单调区间；

（2）若-1＜a＜2（ln2-1），求证：函数f（x）只有一个零点x0，且a+1＜x0＜a+2；

0x1，x2∈［0，x0］且x2-x1＝1，都有|f（x2）-f（x1）|≥m成立，求实数m的最大值.

本题集函数的单调性判断、零点及不等式恒成立问题于一身，具有变量多、综合性强、思维难度大、解法灵活多变等特点，能有效考查我们考生灵活应用所学知识解决问题的能力.因此备受命题人关注，常以压轴题的形式出现在各类考试中.

由不等式恒成立求参数范围或证明不等式是常见题型.解答此类问题的常用策略是将其转化为函数最值问题，但某些函数最值不可求，或在求解中具有一定困难，这就需要我们将问题进行转化，即转化为求最值的范围，从而转化为实际问题的求解.

二、问题解答

1.熟练解题通法

单调性是函数的重要性质，函数的极值、最值、零点等问题的求解均以单调性为基础.求解函数的单调区间，只要把握相应的解题通法即可顺利求解.①求定义域；②求导；③令导数为零，求出导函数的零点；④结合函数定义域判断零点左右两侧导函数的正负符号，进而求出函数的单调区间.若其中含有参数，则需对参数进行分类讨论.分类的层次：先讨论最高次项的系数，再讨论零点的存在性，若存在，还需考虑零点是否在定义域内.若含有两个零点，且零点大小不确定，需要再次讨论.

第（1）问解答：f（x）的定义域为（a，+∞）.f′（x）＝.令f′（x）＝0，得x＝0或x＝a+1.

当-1＜a＜0时，a+1＞0，函数f（x）与f′（x）随x的变化情况如下表：

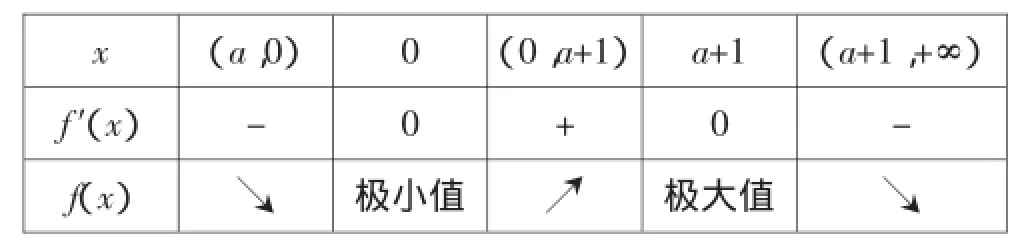
x（a，0）0（0，a+1）a+1（a+1，+∞）f′（x）-0+0-f（x）↘极小值↗极大值↘

所以函数f（x）的单调递增区间是（0，a+1），单调递减区间是（a，0）和（a+1，+∞）.

当a＜-1时，a+1＜0，函数f（x）与f′（x）随x的变化情况如下表：

x（a，a+1）a+1（a+1，0）0（0，+∞）f′（x）-0+0-f（x）↘极小值↗极大值↘

所以函数f（x）的单调递增区间是（a+1，0），单调递减区间是（a，a+1）和（0，+∞）.

2.把握前后关联

导数综合题通常设有多问，解答中注意前后各问之间的关联.第（2）问给出-1＜a＜2（ln2-1），易判断-1＜a＜0，故此问的解答可用第（1）问已得结论，再结合零点定理进行求解.

第（2）问解答：当-1＜a＜2（ln2-1）＜0时，由（1）知，f（x）的极小值为f（0），极大值为f（a+1）.因为f（0）＝aln（-a）＞0，（fa+1）＝-（a+1）2+（a+1）＝（1-a2）＞0，且（fx）在（a+1， +∞）上是减函数，所以f（x）至多有一个零点.又因为f（a+ 2）＝aln2-a2-a＝-a［a-2（ln2-1）］＜0，所以函数（fx）只有一个零点x0，且a+1＜x0＜a+2.

3.最值问题的转化求解

对于不等式恒成立问题的求解，通常转化为函数最值问题.本题“对任意x1，x2∈［0，x0］且x2-x1＝1，都有|f（x2）-f（x1）|≥m成立，求实数m的最大值”可转化为求不等式左边函数的最小值，但零点x0的不确定性，无法求得最值，故应将问题进行转化求解.

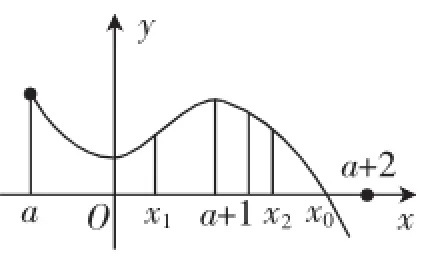
图1

12所以|（fx）-（fx）|的最小值21为.所以使得|（fx）-（fx）|≥m恒21成立的m的最大值为

三、变式演练

变式：已知函数f（x）＝xex-aex-1，且f′（1）＝e.

（1）求a的值及f（x）的单调区间；

（2）若关于x的方程f（x）＝kx2-2（k＞2）存在两个不相等的正实数根

本题无论从命题形式，还是解答方法，与例题有异曲同工之妙.第（1）问也是求函数的单调区间，较为基础.

第（1）问解答：对f（x）求导，得f′（x）＝（1+x）ex-aex-1，所以f′（1）＝2e-a＝e，解得a＝e.故f（x）＝xex-ex，f′（x）＝xex.令f′（x）＝0，得x＝0.

当x变化时，f′（x）与f（x）的变化情况如下表：

x（-∞，0）0（0，+∞）f′（x）-0+ f（x）↘极小值↗

所以函数f（x）的单调减区间为（-∞，0），单调增区间为（0，+∞）.

第（2）问“正数x1，x2是方程f（x）＝kx2-2（k＞2）的两个不相等的正实数根，证明”可转化求不等式左边函数的最小值，但由于方程根的不可求性，最值的求解又落空了.因此，可将问题转化为求x1、x2的范围.解题思路和方法与例题实现完美统一.

第（2）问解答：方程f（x）＝kx2-2，即（x-1）ex-kx2+2＝0.设函数g（x）＝（x-1）ex-kx2+2，求导得g′（x）＝xex-2kx＝x（ex-2k）.由g′（x）＝0，解得x＝0或x＝ln2k.

所以当x∈（0，+∞）变化时，g′（x）与g（x）的变化情况如下表：

x（0，ln2k）ln2k（ln2k，+∞）g′（x）-0+ g（x）↘极小值↗

所以函数g（x）在（0，ln2k）上单调递减，在（ln2k，+∞）上单调递增.

由k＞2，得ln2k＞ln4＞1.又因为g（1）＝-k+2＜0，所以g（ln2k）＜0.不妨设x1＜x2（其中x1，x2为f（x）＝kx2-2的两个正实数根），因为函数g（x）在（0，ln2k）上单调递减，且g（0）＝1＞0，g（1）＝-k+2＜0，所以0＜x1＜1.

同理，根据函数g（x）在（ln2k，+∞）上单调递增，且g（ln2k）＜0，可得x2＞ln2k＞ln4，所以|x1-x2|＝x2-x1＞ln4-1＝

综上，通过对导数的学习和研究，笔者的感悟是导数命题看似常规却不落俗套，看似平淡却富有创新，注重通法又依赖技巧.它启示笔者：在高中数学解题训练中一定要夯实双基，重视数学思想、强调通性通法的训练，加强方法的归纳和总结.同时，要坚持思维训练为中心，强化思维的能力要求，使我们的解题思维达到一定的深度、广度，进而提升我们灵活运用知识解决问题的能力.F