以“问题式教学”进行学力培养与提升的尝试——以中考压轴题讲解为例

2016-05-03江苏省海门市货隆初级中学陈宏亮

中学数学杂志 2016年6期

☉江苏省海门市货隆初级中学　陈宏亮

☉江苏省海门市货隆初级中学陈宏亮

一、问题背景

数学中考压轴题一般指在试卷中出现的大题目，有填空、选择及综合压轴题之分，这类题目难度大，对知识点的综合运用能力要求高.在考试中能拉开学生的成绩，是很多学生和教师重点钻研的专题.对于农村初中学生来说，这是一个不小的挑战.由于农村初中学生结构的特殊性，使得学生学力水平出现两极化现象，学生在课堂上的学力表现产生不平衡性.笔者在课堂上尝试去融合这种不平衡性：先由学力较差的同学进行分析，所有同学进行思考、理解，进行补充或者修正，然后由学力水平较高的同学展示自己个性化的思维过程，其他同学进行补充或者修正，这样，不同学力水平的学生得到了一定程度上的学力培养与提升.笔者以2014年重庆数学中考B卷第18题的讲解为例.

二、课堂实录

实录：题干分析由学力水平较差的同学完成.如图2，连接CG，发现结论：①△EBC≌△GDC；②△ECG、△EHC、△HGC为等腰直角三角形并能求得各边长；③因为CF⊥EG于点H，所以H为EG的中点.

生1：如图2，通过观察图形发现，∠HBC可能是45°，我就作HM⊥AB于点M，那么MH=MB=4，但是H为 EG的中点，MH=AG，所以AG=8.因为AD=6所以DG=BE=2.同时连接EF，则EF=FG，可以设FG为x，那么AF=（8-x）.又AE=4，根据勾股定理可列方程（4-x）2=x2，进而求出FG，只是∠HBC=45°，原因是什么，我不知道，但是直觉上感觉应该成立.

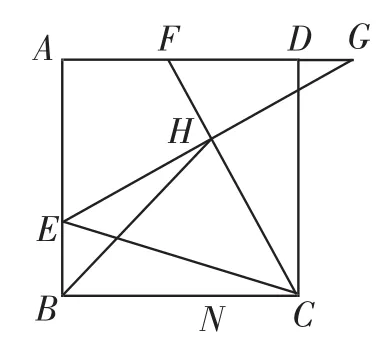
图1

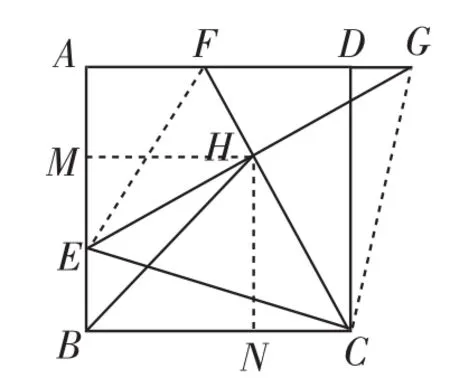
图2

师：对于∠HBC=45°是否成立，小组内共同分析图形，能否找到图形模型，进而解决问题，一起分享一下.给大家3分钟时间.

生2：我发现两个垂直，就是∠EBC=∠EHC=90°，那么B、E、H、C四点共圆，∠HEC和∠HBC为同弧所对的圆周角，相等，因此∠HBC=45°.

生3：如图2，我从以前做过的题目中发现一种方法，由于HE=HC，那么我作HN⊥BC，这样△HME≌△HNC，四边形MBNH为正方形，同样可证.

师（总结）：解决这一问题的时候我们有什么收获？

生4：当我们在解决难题时，需要对图形分析透彻，可以联想到我们积累的图形模型，添加恰当的辅助线，进而解决问题.

师：在解题中，我们解题时运用了题干分析中的H 为EG的中点，进而利用三角形的中位线解题，那么对于中点的运用还有哪些方法？小组讨论后，全班展示分析过程，并总结所运用的知识点.给大家5分钟时间.

小组1：如图3，建立直角坐标系，既然点H是EG的中点，设BE为x，则点E（0，x）、G（6），则H的坐标为根据∠HBC=45°，可得H的坐标为（4），所以3，则BE=2，求FG的过程同生1.我们运用了直角坐标系中的中点坐标公式.

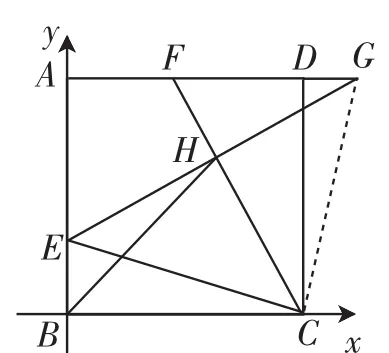
图3

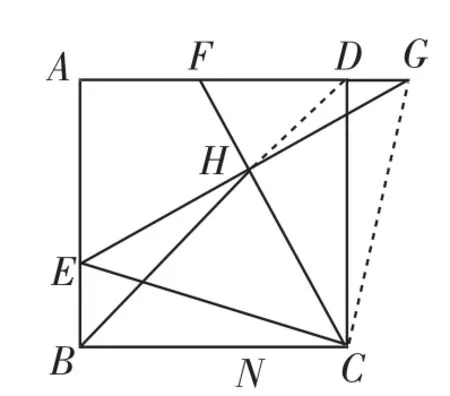
图4

小组3：对于求FG，我们的方法没有那么巧妙，但是很实在，我们是通过计算得来的，BE=2，所以AE=，我们可以利用△FHG∽△EAC，或者利用同角的三角函数值相同求解.我们小组发现图中存在“斜截型相似”（新授课时学生对于模型的总结）.

小组4：如图4，我们小组没有利用中点，刚才已经证明∠HBC=45°，延长BH，一定通过点D，BH=8，BD=12，所以，我们小组认为既然有45°，那么可以运用正方形的对角线构造“X型”相似.

还有小组构造了梯形的中位线，以及运用一条直线过矩形的中心，则矩形面积被平分来求解，同样能解决，图形及过程相对复杂，在此就不阐述了.问题讨论过程中，以往积累的知识与方法被不断地回忆、运用、展示，其他同学在倾听与思考过程中不断进行模仿与运用.在小组展示后，还对知识点的运用进行总结，整个学习过程中，不同学力水平的学生的学力得到了一定的提升（正确解决本题的只有5位同学，课后同类型练习中大家的分析能力明显变强）.

三、后记

“课程标准”指出，数学课堂中应对学生提出问题和分析问题、独立思考问题、与他人合作交流、尝试从不同角度思考问题、有条理地表述自己的思考过程、倾听和理解别人的思路、反思自己思考过程的意识培养等方面予以关注，而串联这些能力的媒介就是“问题”，在本堂课中其实只有三问.①∠HBC=45°是否成立？如何证明，②分析图形，寻找图形模型，③中点如何运用.围绕这三个问题，学生进行思考并有效解决了本题分析的难点.在讲解压轴题时，笔者认为进行有效的问题设计是关键，在《以“问题式”教学寻求几何解题思路的尝试》一文中，笔者采用了梯度式问题设计，这种设计有效延长了学生的思维历程，让学生在知识理解上更有效，较适用于新知的学习.而本例中则采用了结点式问题设计：对于即将参加中考的初三同学来说，知识、方法、能力已经有了一定的储备，只是在处理压轴题时不能有效提取知识储备，这种设计的优点在于自主提取知识储备，有效提高知识的运用熟练度.因此此时采用结点式问题设计较为妥当.笔者认为有如下几种处理方式.

以生疑为问：以学生产生疑问的知识结点设问并暗示出解决方向.处理本例时，笔者让同学们分析图形，从常用图形模型中就能找到解决问题的途径.

以知盲为问：以学生的知识盲区设问，笔者常用“生问生答”的方式处理.学生对于知识点本身就不知道，探究或者引导已无意义，因此“生问生答”能很好地利用学生知识上的互补性.

以图型为问：当几何图形过于复杂时，引导学生分析图形，发现图形模型，进而利用图形模型进行解题.

以法型为问：当无从入手时，尝试分析解决问题的方法模型，进而解决问题.

以题眼为问：问题思维起点不一样，解题方法可能就多样，因此对于题眼的有效把握至关重要，本例中就主抓中点的运用，当然也有同学主抓特殊角度利用相似解决.