生长型构架下实数复习课的教学实践与思考

☉江苏省南京市宁海中学分校　卜以楼



生长型构架下实数复习课的教学实践与思考

☉江苏省南京市宁海中学分校卜以楼

近日，笔者在“第39届浙派名师暨全国初中数学名师经典课堂教学艺术展”活动中，演绎了一节“实数”复习课.这节课以生长型构架为理念，智慧地、立体地呈现数系及其运算发生、发展的过程，不留痕迹地再创数学运算发展进程，由浅入深，由易到难，循序渐进展开教学活动，为单元复习课的教学打开了一个创新的通道.本文拟对这节复习课的教学价值、活动设计及实践反思作一个简单梳理，现与同仁们交流，以期得到更多、更好单元复习课的教学成果.

一、生长理念下复习课的价值判断

1.对教材体系编排的基本认识

实数这部分内容，在不同的版本中被安排在不同的学段、不同的章节.如“青岛版”安排在八（下），将“实数”安排在“勾股定理”之前.“苏科版”“北师大版”“湖南版”“华师大版”“湖北版”等都安排在八（上），且“苏科版”“北师大版”将“实数”安排在“勾股定理”之前，“湖南版”“华师大版”“湖北版”将“实数”安排在“勾股定理”之后.“人教版”“上教版”“上科版”等将“实数”安排在七（下），且都将“实数”安排在“勾股定理”之前.只有“浙教版”将“实数”安排在七（上），将“实数”安排在“有理数的概念”和“有理数的运算”之后，成为初一学生学习数学的第三章内容.

教材这样安排各有千秋.将“实数”安排在八（下），能让学生在已有“勾股定理”这个知识贮备和经历过三个学期的学习经验积累下，更加深刻地认识实数.安排在八（上）并且将“实数”编排在“勾股定理”之后，也是为了让学生用正方形的面积和勾股定理这两个路径来认识实数.安排在八（上）和七（下）并且将“实数”编排在“勾股定理”之前，则是为了让实数为运用勾股定理解决问题提供必备的知识支撑.而安排在七（上），让“实数”成为初一学生学习初中数学的第三章内容，这样的编排，可以让学生借助刚学完的有理数系，自然地将数集延伸到无理数系、实数系，符合最近发展区理论和知识系统化理念，唯一不足的是刚上初一的学生认知心理和知识基础对研究实数来说略显稚嫩.

2.对实数复习课教学的价值分析

“如果说新授课是数学教学的‘画龙’之作，那么复习课则是‘点睛’之处.而在实际教学中，复习课往往上成了新授课的再现，时有‘炒冷饭’之嫌，影响了复习课的效益，阻碍了学生在复习课上进一步发展”［1］.基于上述对教材编排体系的认识、浙教版教材的编排特点及复习课功能，对浙教版教材下实数复习课的价值作如下分析.

（1）让学生学习经历成长.

实数这一章内容，知识比较零散，它有开方运算、方根概念、无理数和实数概念及分类、实数的表示方法、实数的运算、近似数及估算等知识.这些知识如果处理得不好，那么就只是新授课的一个机械重复，学生只能在已有的知识上团团转，不会在更高的思维层次上得到更好的发展，特别是对于基础较好的学生，他们基本上得不到更多的收获，而对于基础相对薄弱的学生，也只能是在复习的过程中靠记忆来获取一些零散的知识，这样的复习显然不会出现理想的效果.

笔者认为，复习课除了要对所学的知识进行查漏补缺，还要让学生所学的知识结构化，以凸显“让学生又一次发展”的教学理念.如何在教学中实践这一理念，需要教师智慧地整合教学资源.就浙教版教材下实数复习这一内容而言，一是要根据初一学生知识贮备有待进一步提升的教学实际，有效选择学材；二是要根据学生刚进入初一数学学习的起步阶段，学生身心与初中数学学习需要进一步调整的教学实际，合理选择方法.根据这两个基本诉求，“数系及其运算”这一能够让学生成长的主题进入了笔者的教学视野.即让学生根据小学学习过的加法、减法、乘法、除法和初中刚学习过的乘方、开方这六种运算，经历数及其运算的发生、发展进程，感受数系的扩展过程，让学生与数学知识一起成长，并在此过程中感受无理数的本质，体验数学的发展与人的思维发展的协同性、一致性与和谐性.

（2）让数学思维讲述故事.

数学教学在某种程度上说就是数学思维的教学，数学活动就是用数学思维讲述数学故事，凸显数学主题，体悟数学道理，让学生在数学课上有数学的获得感.可以这样认为，讲述数学故事就是构建一个生动活泼的、主动的和富有个性的过程，也是“一个思维层层递进、论证步步为营、收获粒粒归仓的学习场”［1］.要让课堂讲述数学故事，那么就必须设计好一条主线，在这条主线上来开展数学思维活动，上述确定的“数系及其运算”这一主线恰好能担负起这样的教育功能.数的运算，从结果上看，往往能达到“数怎么又不够用”的思维效果，这正是数学思维所要讲述的数学故事.

（3）让复习课堂走向远方.

怎样让复习课上得有新意、有品位，怎样让复习课走向远方？这是个值得探究的“老”课题.笔者认为，坚守“让复习课不再是新授课的机械重复，而是复习课的思维提升；不再是复习课的平面增长，而是活动课的理性探究；不再是活动课的单一探究，而是数学课的光芒万丈”［1］的教学理念，并不断践行这些理念，才能使复习课走向远方.就这节课来说，不应是些散件的简单堆砌，而应是知识的逻辑生成，让学生感受无理数、实数与以前学过的有理数一样，它是实实在在、真真切切存在的，让学生明白无理数、实数究竟是一些什么样的数，让学生会用无理数、实数去解决问题，让学生运用无理数、实数去讲新的数学故事.能做到这些，就是将学生从课堂中带向远方，这样的课堂就有范儿.

二、价值判断下实数复习课的构架

基于上述的教育理念，笔者在教学中设计了下列教学活动，来凸显实数这节复习课的教学价值.

开头话：今天和同学们复习第三章“实数”这一内容.这节课老师为同学们准备了一张长方形的纸片，现在我们就从这小小的长方形纸片开始这节课的复习之旅.

【设计意图】开门见山，直接点明这节课需要复习的内容，需要借助的载体，需要解决的问题，让学生心中有数，让目的更明确.

活动1如下所示.

回忆与思考：如图1，一张长方形纸片，长为1.5，宽为1.

图1

问题1：长与宽的和是多少？

【设计意图】让学生用加法来解决这个问题，并通过下列预设生成中的追问，开始本节课的行程之旅，以此来讲述思维故事.

【生成预设】如果学生回答是2.5，可追问学生，你是怎么得到这个结果的.待学生说出1.5+1=2.5时，再追问，你能将这个算式用字母表示出来吗？逼学生得到a+b=c.继续追问，在这个算式中，如果知道c和a（或b），求b（或a），该如何列式计算呢？逼学生得到算式c-a=b（或c-b= a），再继续追问，加法的结果叫什么？减法的结果叫什么？加法和减法这两种运算是什么关系？

在上述活动中形成下列板书：

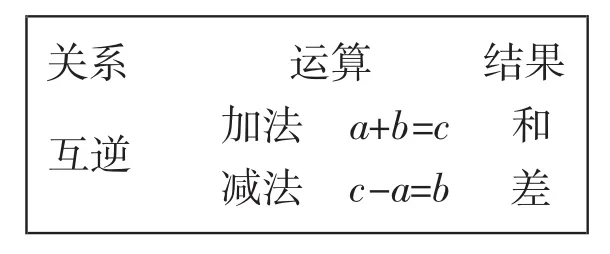
关系　　运算　　结果加法　a+b=c和减法　c-a=b 差互逆

问题2：这个长方形的面积是多少？

【设计意图】本问题的设置意图同问题1.

【生成预设】同样，在这个活动中也要形成下列板书.

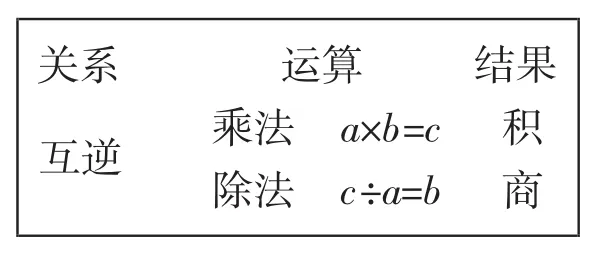
关系　　运算　　结果乘法　a×b=c 积除法　c÷a=b 商互逆

问题3：将此长方形按图2所示，折出一个边长为1的正方形，则正方形的面积是多少？

图2

【设计意图】通过本问题，将运算的视角引入到乘方运算，并通过如问题1中的生成预设，让学生感受乘方与开平方互为逆运算.即让学生感受开方运算同小学学习过的减法运算、除法运算一样，分别是乘方运算、加法运算、乘法运算的逆运算.通过这样的活动，降低对开方运算的认识难度，同时让学生感受数学中的某些规则同生活中的规则一样，往往具有一致性、相容性、和谐性.

【生成预设】如果学生用算式“1×1=1”来计算面积，可追问还可以将“1×1=1”写成什么形式，逼学生说出可以写成“12=1”的形式，进而得到“a2=b”的一般形式.

通过上述活动，同样要形成下列板书的形式.

关系　　运算　　结果乘方　a2=c　 　　幂开方　a=± c互逆■　　平方根

类似地，还可以得到开立方运算、立方根的概念.

活动2如下所示.

操作与思考：如图3，将边长为1的两个同样的正方形拼成一个新正方形.

问题1：这个新正方形的边长是多少？

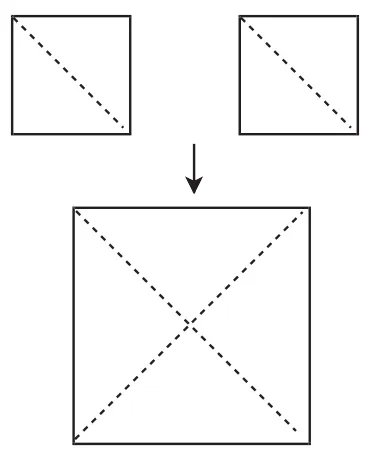
图3

【生成预设】如果学生不会求新正方形的边长，可启发学生，拼成的新正方形的面积可求吗？进而让学生通过新正方形的面积求出边长.

【设计意图】让学生感受并体会无理数与有理数一样，也可以在数轴上表示出来，反之数轴上的点表示的数可能是有理数，也可能是无理数，从而进一步理解“数轴上的点与实数是一一对应的”这一结论.

【设计意图】通过这个问题，让学生再次感受无理数的绝对值的意义.

活动3如下所示.

探究与思考：如图4，我们沿边长为1的正方形的对角线剪出一个等腰直角三角形，给它起一个名字叫三角形ABC，沿CE折叠三角形ABC纸片，使A点落在BC边上的D点处.

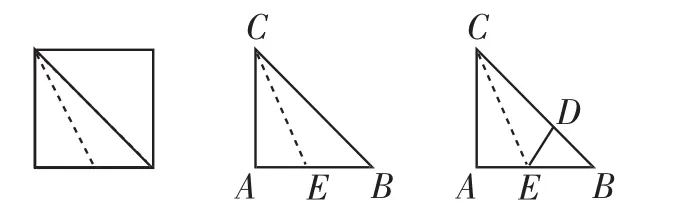
图4

问题1：求BD的长度.

【设计意图】让学生在操作的过程中，感受实数的运算.

【生成预设】如果学生不会求BD的长度，可再次让学生感受操作的过程，并提出问题：在折叠的过程中，重合的线段，在数量上表示什么意思？

问题2：继续折叠，使点B与点D重合，折痕为FQ，请你求出此时线段DQ的长度，并比较此时DQ的值与的大小关系.

图5

【设计意图】一是继续延伸解决问题1的经验，求出线段DQ的长度为；二是深化估算的思想，合理选择比较大小的方法，对学生进行“算理”的再教育.

结束语如下所示.

延伸与思考：本节课，我们从互为逆运算的角度，重温数系的发展进程，重走发现之路，讲述数学故事.下课后，请同学们继续思考：对于an=b，我们知道，若给出a、n，求b，是乘方运算；若给出b、n，求a，则是开方运算；若给出a、b，求n，你怎样来思考这种新的运算呢？

【设计意图】在学生感受了加法、减法、乘法、除法、乘方、开方六种运算的发展过程后，再次将学生研究运算的视角延伸到一个新的背景之中，让学生感受到要研究这种运算的必要性和可能性.接下来就要发挥学生自己的聪明才智，定义这种运算的规则和方法了.设置这样一个开放的空间，就是让学生延续本节课研究运算的一般方法与规律，让不同的学生在数学上都能得到良好的发展.所要注意的是，不是将高中的“对数”运算全盘下放到这里，而是让学生有一种研究运算的意识呈现，有一种怎样定义运算的方法倾向，有一种研究问题的经验积累，这才是教学的价值之所在.

三、生长构架下复习课的实践思考

生长型构架理念下的复习课，是一个让学生在更高视野下构建知识的过程，也是一个让学生在更深思维下感受生长的过程，还是一个让学生在更精文化下发展自我的过程，在实际操作中，要在以下四个方面谋篇布局.

1.要选准一条主干

用生长型构架进行复习，“要有打破教材结构的勇气，深刻反思和总结教学中相近或相邻的知识，从知识体系和知识结构上去把握初中数学教学内容和教学要求”［2］，要选准一条复习的主干.这条主干，要根据复习的知识、已学习过的知识和将来要学习的知识，在学科系统内有机融合、整体构建、创新方式、有效推进.要分析所复习知识的地位，要提炼所复习知识的思想，要梳理所复习知识的脉络，要创新复习知识的方法，要把握所复习知识的发展方向.

本课例的设计就是从上述几个维度打磨而成的.具体地讲，根据要复习的知识中存有开方运算，根据开方运算的结果可能产生无理数的基本事实，下通小学学习过的加法、减法、乘法、除法四则运算，平转到初一刚学习过的乘方、开方两种运算，上达高中将要学习的“对数”运算，这在数学中本身就是一条发展的主线，只不过受学生身心发展规律的影响，受学生学习知识的限制，受教材编排体系的左右，让这条本来显性的主干隐性化了，从而导致学生学到的知识碎片化，其结果往往是只见树木不见森林，削弱了所学知识的整体化、结构化、经验化、能力化.为此，在教学过程中，要有意识地让学生补好上述所缺失的那一课，而生长型构架的复习课能为之提供有效的互补养分，也能给学生提供再次发展的力量，这也是生长型构架复习课的价值形态.

2.要突出一个主题

现在的课堂中学生的主体意识得到了强化，但是也不能过分削弱教师的主导作用，更不能削弱数学思维这一数学学习的主题.不管数学教学改革怎么进行，课堂上的所有活动，都应该凸显数学思维活动，这才是永恒不变的教学主题.说到底，数学教学就是数学思维的教学，它是一个颠簸不破的真理.有了复习主干，只是提供了一个宏观的东西，在围绕主干上寻求思维载体，设计积极的、有效的思维活动，方可见英雄本色.

本课例中，智慧地选择一个长方形的纸片，作为凸显主干知识的载体，在这条主干上开展思维活动，是本课例的匠心所在.不断折叠此长方形的纸片，就是不断变换问题背景，在变换的背景中，引发学生的思维，激发学习的兴趣.从长方形到正方形，从正方形到等腰三角形，从等腰三角形到最后的四边形，就是让学生通过自己的思维活动，认识开方运算的本质，认识平方根、立方根的意义，认识有理数、无理数的本质.具体地讲，就是让1、这些有理数、无理数有序登场，最后要求学生估算，让学生根据算理，得到“由于1＜＜2，所以0＜-1＜1，则0＜”这样一个高级思维推理活动，目的就是基于算理，回归估算；基于本真，止于本质.上述各个层次的思维设计，不断地将讲述的数学故事推向高潮，将开展的数学思维推向高峰，将积淀的数学文化推向高端.

3.要经历一次生长

教育的出发点和落脚点就是让学生经历一种成长、见证一种成长.生长型构架的复习理念本身就是一种让学生在复习课中成长的理念，一种让学生在复习课中成长的策略.

本课例中，从小学学过的加、减、乘、除四则运算，到初中刚学习的乘方、开方运算，再到高中将要学习的对数运算，这些节点的构建，就是让学生在学习过程中形成明显的生长节，注定会成为学生学习、复习实数的生长烙印，永记心中.不仅如此，而且还会让学生对后续学习的对数运算产生美好企盼.

4.要实现一眸回顾

对复习内容进行结构化、系统化，可以让学生有一览众山小的感觉，还可以降低学生学习数学的畏难情绪，有利于学生对数学学习产生亲近感.

本课例针对初一新生对开方运算和无理数学习过程中产生的理解不到位的偏差，让学生从非常熟悉的小学四则运算出发，通过不断变化手中的长方形纸片，引导学生开展积极的思维活动，让学生拾级而上，观赏数学运算风景，讲述无理数的故事，当到达山峰时，俯首回眸，开方运算与无理数的芳容尽收眼底，实数的知识结构一目了然，学生自然得到“一眸回顾，一份心慰”的情感体验，尽收一幅数学的天然画卷！

参考文献：

1.卜以楼.让复习课留下一串串生长节［J］.中学数学月刊，2013（11）.

2.卜以楼.用生长型构架进行中考二轮复习［J］.中国数学教育（初中），2010（3）.