一道课本习题证法的讨论、拓展与应用

☉安徽省六安皋城中学　陈　炎



一道课本习题证法的讨论、拓展与应用

☉安徽省六安皋城中学陈炎

一、问题提出

如图1，已知反比例函数y1=在第一象限的图像，过y2上的任意一点A，作x轴的平行线交y1于B，交y轴于C，过点A作x轴的垂线交y1于D，交x轴于E，连接BD、CE，则=_________.

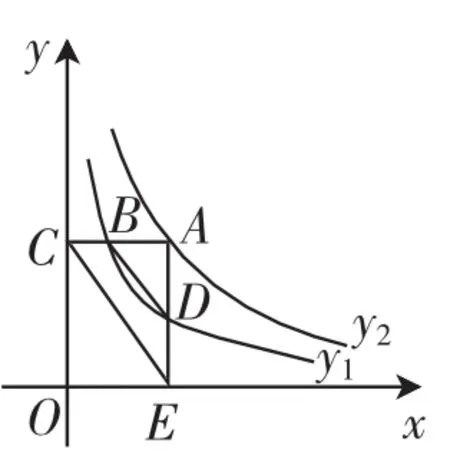
图1

此题是沪科版教材九年级上册第21章《二次函数与反比例函数》的复习题.题目是反比例函数综合题，主要考查曲线上点的坐标与方程的关系，反比例函数的系数k的几何意义，相似三角形的判定和性质.题目难度适中，解决方法不唯一，能很好发散学生的思维，锻炼学生解决数学问题的能力.

二、问题讨论

笔者查阅了不少资料，发现基本上千篇一律都是采取如解法1的方法：通过引入参数，建立横、纵坐标之间的关系，然后利用三角形相似来解决.

解法1：参数法.

设A点的横坐标为a，把x=a代入y2=，得y2=，则点A的坐标为.因为AC⊥y轴，AE⊥x轴，所以C点的坐标为，B点的纵坐标为，E点的坐标为（a， 0），D点的横坐标为a.

因为B点、D点在y1=上，所以当y=时，x=；当x=a，y=.所以B点的坐标为，D点的坐标为）.所以AB=a-，AC=a，AD=，AE=

当然，本题通过利用反比例函数“k”的几何意义来解，也很方便.

解法2：利用“k”的几何意义.

过B点作BF⊥x轴，垂足为F，过D点作DG⊥y轴，垂足为G，BF与DG相交于H.则S四边形OCBF=S四边形OGDE，所以OF· CO=DE·OE，所以BC·（AD+DE）=DE·（AB+BC），即BC· AD+BC·DE=DE·AB+DE·BC，得到BC·AD=DE·AB，所以.又因为∠BAD=∠CAD，所以△BAD∽△CAE.所以

但是，学生尚未接触到相似的知识（相似形知识在第22章），如何解？就学生的现状来说，需回避相似，因而有下面的解法.

解法3：勾股定理法.

在解法1（*）以下的解题过程中，可以这样处理.

在Rt△ABD中，BD2=AB2+AD2=

在Rt△ACE中，CE2=AC2+AE2=a2+

三、解后反思

通过以上解法1和2的对比，我们可以发现：本题的解法很好地体现了从“数”和“形”两个角度来思考和解决问题，正如我国著名数学家华罗庚先生曾经说过：“数形结合百般好，隔裂分家万事休.”“数形结合”思想在解决反比例函数和初中阶段的其他函数问题中，都具有广泛的应用，是处理函数问题的重要方法.数学教师不可回避要讲解题目，题目怎么做？为什么这样做？怎么想起来这样做，今天这样做的，下次遇到此类问题是否还能想起来这样做？还可以怎么做？这道题老师怎么讲，学生先讲还是老师启发式先铺垫……诸如此类问题，应是广大一线教师要不断思考的问题.

在解这道习题时，笔者颇感利用相似的知识在处理本题时的巧妙性和简洁性.笔者查阅了不少“课本解题手册”，几乎都是用相似法（解法1、2的后半部分）解决的.但是按照课本的章节设置，第22章是相似形，学生尚未学习到，所以笔者在讲解、分析这道题时，总感觉不畅快.一方面，不用相似法，似乎这道题的“生命价值”并没有完全显现出来.《义务教育数学课程标准（2011版）》强调：学生是数学学习的主体，在积极参与学习活动的过程中不断得到发展.以学生为主体，以学定教，教师的教学活动要特别重视学生已经知道了什么，关注学生的最近发展区.笔者妄揣，教材的编写专家是否想借助本题，发挥“承上启下”的功能，即对下章学习起到铺垫作用？另一方面，笔者大胆建议，此题是否可以放到教材第22章的习题中去，这样可以更好地体现反比例函数与相似的“强强组合”.敬请教材专家和同行不吝批评指正.

四、拓展研究

解决本题以后，笔者进一步研究发现：双曲线与矩形“缠缠绵绵”，有不少“背后的故事”，需要深度挖掘.

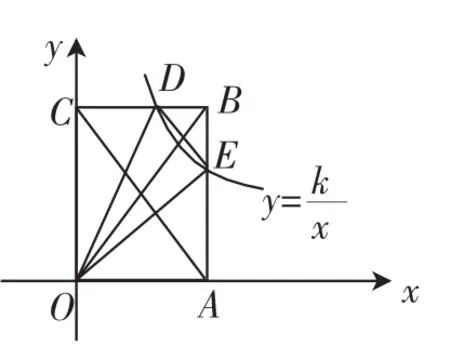
图2

拓展5：S△OBD=S△OBE.

五、应用

例1（2015年徐州））如图3，在矩形OABC中，OA=3，OC=5，分别以OA、OC所在直线为x轴、y轴，建立平面直角坐标系，D是边CB上的一个动点（不与C、B重合），反比例函数y=（k＞0）的图像经过点D且与边BA交于点E，连接DE.

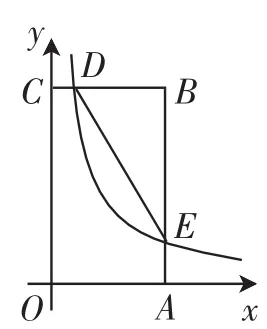
图3

（1）略.

（2）连接CA，DE与CA是否平行？请说明理由.

例2（2015年甘南州）如图4，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，A、C分别在坐标轴上，点B的坐标为（4，2），直线y=-x+3交AB、BC于点M、 N，反比例函数y=的图像经过点M、N.

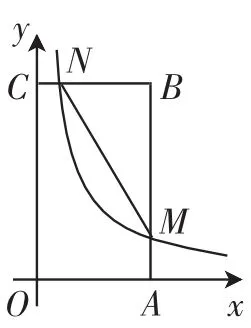
图4

（1）略.

（2）若点P在x轴上，且△OPM的面积与四边形BMON的面积相等，求点P的坐标.

例3（2012年成都）如图5，在平面直角坐标系xOy中，直线AB与x轴、y轴分别交于点A、B，与反比例函数y=（k为常数，且k＞0）在第一象限的图像交于点E、F.过点E作EM⊥y轴于M，过点F作FN⊥x轴于N，直线EM与FN交于点C.若（m为大于l的常数），记△CEF的面积为S1，△OEF的面积为S2，则=________.（用含的代数式表示）

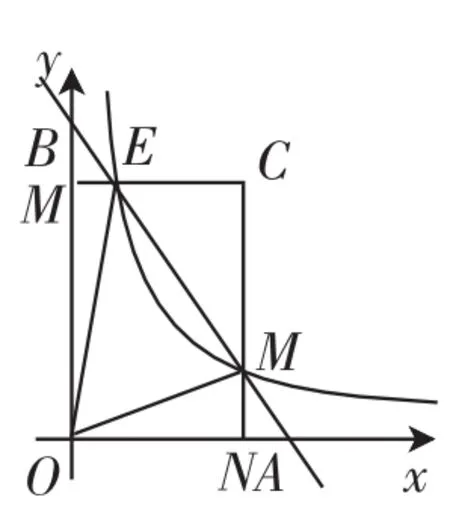
图5

六、思考

教材是教学的原本，教教材还是用教材教？这一问题数学界已经提出很多年了.综观近几年的中考命题，愈发觉得试题的素材来源于课本倾向明显.这就要求我们引导学生从题海中上岸，回归课本、重视课本，创造性地使用课本，真正落实减负增效.教师在完成对文本内容的教学之余，如果能多从书本后的习题入手，把看似平常的问题，拔高、延伸、拓展，“深挖洞，广积粮”，那么看似“平静”的教材必然可以“灵动”起来.

参考文献：

1.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.