例谈不等式恒成立求参数范围的有效策略

☉江苏省如皋市第二中学 黄荣

例谈不等式恒成立求参数范围的有效策略

☉江苏省如皋市第二中学 黄荣

不等式恒成立问题是高中教学重点之一，近几年已经成为高考必考点，根据不同不等式恒成立问题，求出各个参数的范围是一种较为常见的问题，主要表现在以下几个方面：（1）在给定区间上，不等式恒成立；（2）不等式的解集为全体实数；（3）解析式的值恒大于（等于或小于）某值；（4）函数的定义域为全体实数.由于此类问题知识覆盖面较广，综合性很强，对解题的灵活性要求高，因此对同学们来说有较大的难度.思维要求高，技巧性强，学生不易把握，若能充分挖掘题目特点，采用合适的方法，往往能迅捷、巧妙地找到解题的突破口.

一、更换主元法

针对不等式恒成立问题，解决策略较多，其中构造适当的函数是一种最重要的思想方法之一，这种思想充分利用函数的图像和性质来解决不等式问题，数学问题中含有多个变量，就需要确定合适的参数及变量，探讨各个变量之间的关系，使不等式问题更加清晰.在求解中，一般是通过已知变量范围，来求另一个变量的范围.

例1对于满足0≤p≤4的一切实数p，不等式x2+px＞4x+p-3恒成立，求x的取值范围.

解析：设f（p）＝（x-1）p+x2-4x+3，当x＝1时，显然不满足题意.

由题设知，当0≤p≤4时，f（p）＞0恒成立，所以f（0）＞0且f（4）＞0，即x2-4x+3＞0且x2-1＞0.解得x＞3或x＜-1.所以x的取值范围为x＞3或x＜-1.

评注：习惯上把x当作自变量，记函数y＝x2+（p-4）x+ 3-p，于是问题转化为当p∈［0，4］时，y＞0恒成立，求变量x的范围.在求解x的范围时，利用建立函数思想，通过二次函数及二次方程实根分布原理，依照这个思想进行计算的话，问题解决非常复杂.在问题解决中，将x与p两个变量互换一下，将需要求解x的范围看作一个常量，则这个题目就转化为p的一次函数大于0在［0，4］范围内关于恒成立的问题.

二、利用必要条件缩小范围

有一类题直接讨论解答比较烦琐，可以利用题中的必要条件缩小范围，避免了讨论，有着意想不到的简洁.

例2设函数fn（x）＝-xn+3ax+b（n∈N*，a，b∈R）.若x）|在［-1，1］上的最大值为，求a，b的值.

解析：f4（x）＝-x4+3ax+b（n∈N*，a，b∈R）.

评注：不等式对x∈D恒成立，我们在D中选取特殊值代入不等式，可以缩小参数的范围，避免分类讨论，甚至也可以直接得到答案.

三、利用二次函数的判别式

不等式恒成立问题，可用判别式来求解，这个思想在求解中比较常用.

所以Δ＝（6-2m）2-8（3-m）＜0，解得1＜m＜3.

故实数m的取值范围是1＜m＜3.

评注：一般地，二次函数f（x）＝ax2+bx+c 恒正f（x）＝ax2+bx+c恒负⇔

四、利用分离参数

若原题较容易分离出变量，而另一边为常见函数，则可转化为这些常见函数的最值问题求解.

例4设函数f（x）＝lnx+ln（2-x）+ax（a＞0），若f（x）在（0，1］上的最大值为，求a的值.

评注：（1）已知函数f（x）在x∈D上的最值，转化为不等式f（x）≤M（或f（x）≥N）恒成立，如果不等式能进行参数分离，等价变形为a≤g（x），则a＝g（x）min；等价变形为a≥g（x），则a＝g（x）max.

（2）若改变条件“a＞0”为“a∈R”，上述解法不受影响，但若用常规方法，在求函数f（x）的导函数的零点时，要对a进行分类讨论，过程烦琐复杂，难度较大，由此显示上述转化法的简洁美！

五、构造函数法

将不等式恒成立构造出函数，分析函数性质，然后再解决问题.

所以f（n）是关于n（n∈N，n≥2）的递增函数，则f（n）

评注：在这个不等式中，有关n的式子全部在不等式的左边，利用函数观点分析，不等式的左边看作关于n的函数，这就要求函数值的最小值大于1，因此，题目转化为求函数的最小值，可以从分析函数的单调性角度出发来进行解决.

六、利用数形结合，化抽象为直观

如果改变思考和观察问题的角度，采用数形结合的方法求解不等式恒成立中参数的范围，不仅能使问题化抽象为直观，而且可取得避繁就简的效果.

例6已知函数f（x）＝ex-ln（x+m），当m≤2时，证明f（x）＞0.

证明：当m≤2时，要证明f（x）＞0，只需证ln（x+m）＜ex.

由于函数g（x）＝ex是下凸的，h（x）＝ln（x+m）是上凸的.

设g（x）＝ex与h（x）＝ln（x+m）切于点P（x0，y0），

于是由图像（图1）可知，要使ln（x+m）＜ex，只需h（x0）＝ln（x0+m）小于切点的纵坐标.

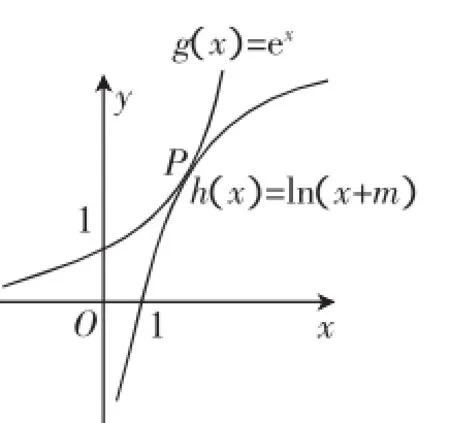
图1

若x0＝-1，则m＝2.

故当m≤2时，f（x）＞0.

评注：通过数形结合，揭示了含参数不等式恒成立问题实质上体现了函数、方程、不等式之间的有机联系，结合图形，灵活转化，选择最佳解题策略.

可见，从多角度、多方位研究问题，往往能激活思维潜能，充分挖掘思维潜力，解题中，让人耳目一新，产生意想不到的收获.

总之，在我们解决恒成立问题时，我们要注意区分与“能成立”、“恰成立”概念的不同之处.并且掌握解决它们的常用方法：分离变量法、数形结合法、分类讨论法、判别式法、构造函数法等.但是，此类问题种类较多，因此解决方法往往有多种，难度比较大，在日常解题中，需要逐渐提高思维灵活性和创造性.因此，我们要不断在训练中强化理解，及时总结、领悟、提高.F