巧解一类含参数的线性规划问题

☉湖北省秭归县第一中学 胡俊

巧解一类含参数的线性规划问题

☉湖北省秭归县第一中学 胡俊

含有参数的线性规划问题或二元一次不等式（组）问题，对于学生而言，既是一个难点，又是高考的一个常考点，高考对这类问题的考查可谓常考常新.学生解决这类问题之所以感觉困难，主要是因为这类问题含有参数从而使得要解决的问题处于动态变化之中，学生要么不知如何动笔，要么针对参数进行分类讨论时对变化因素考虑不周全而出错.那么，对于此类问题有没有简洁有效的解决方法呢？笔者通过对一道高考试题的深度挖掘，得到一种解决含参数的线性规划问题或二元一次不等式（组）问题的简洁方法，与各位同仁分享.

①∀（x，y）∈D，x+2y≥-2；②∃（x，y）∈D，x+2y≥2；

③∀（x，y）∈D，x+2y≤3；④∃（x，y）∈D，x+2y≤-1.

其中的真命题是___________.

一、试题解析

简析：注意到四个命题均为研究x+2y的取值范围，故转化为研究目标函数z=x+2y的最值问题.通过画出可行域（如图1），结合中z的几何意义容易求得zmin=0，即z≥0.

因此，命题①、②为真命题.

图1

二、反思升华

本题属于常规问题的创新，从全称、特称命题的角度考查了线性规划中的最值问题.试题难度不大，学生基本能正确解答.但仔细回味，我们对本题会有更深的理解：从代数角度来看，z有最小值0，也就是说x+2y≥0对于任意的（x，y）∈D恒成立.而从几何角度来看，我们可以这样理解：原不等式组所表示的区域D应该包含于x+2y≥0所表示的区域（或者区域D在直线x+2y=0的上方）.本题的四个命题正是用代数语言刻画了这种包含关系.相对于代数不等式的抽象表示，利用平面区域间的包含关系能够让我们直观地明确相应直线与平面区域的位置关系，这对于含有参数的线性规划问题或二元一次不等式（组）问题不失为一种简洁有效的方法.下面我们通过对几个具体例题的分析解答，详细说明这一解答方法.

三、举例应用

分析：按常规解法，先画出可行域，再寻求平行直线系y=-ax+z的纵截距何时最大.这就需要对斜率-a进行分类讨论，从而确定目标函数所对应的直线，然后将最大值用a表示出来，进而构造关于a的方程以求出a值.此法由于涉及分类讨论且在不同情形下直线的方向在不断改变，学生很可能顾此失彼.若利用平面区域间的包含关系则可以避免讨论，整个解题过程显得简洁流畅.

解：根据约束条件作出可行域，如图2所示.由ax+y≤4对于可行域内任意点恒成立，即整个可行域应该位于直线l：ax+y=4的下方.其中直线l恒过点（0，4），同时由于ax+y≤4要取到等号，即直线l与可行域要有公共点，则由图2易知直线l一定过点A（2，0），将点代入直线l的方程则有2a=4，得a=2.

图2

分析：与例1一样，若按部就班地作出可行域与目标函数对应的直线系后再求解，则不可避免地要针对k的范围进行分类讨论.而运用平面区域间的包含关系则可以直接求解.

解：由题知整个可行域应包含于y-x≥-4内部，且应与直线y-x＝-4有公共部分.我们首先作出不等式y-x≥-4表示的区域（直线上方），再作由约束条件表示的可行域，如图3所示.注意到直线kx-y+2＝0恒过点（0，2），则要满足题意只能是直线kx-y+ 2＝0过点A（4，0），代入可求得k＝-.

图3

评注：以上两例中，我们利用平面区域间的包含关系分别解决了线性规划问题中的两类典型含参问题：（1）约束条件含参；（2）目标函数含参.从整个解答过程来看，将最值条件转化为不等式恒成立后，再利用平面区域间的包含关系解决是行之有效的.实际上，这种解法对其他形式的含参数的不等式问题也大有用处.

例3（2015年高考重庆卷）已知函数f（x）＝|x+1|+ 2|x-a|的最小值为5，则实数a＝________.

分析：本题如果考虑去掉绝对值符号，转化为分段函数求解的话，则需要对a进行讨论，难度较大.与上两例一样，我们可以将问题转化为不等式恒成立问题，从而通过构造图像加以解决.

解：由题意知，要使2|x-a|≥5-|x+1|对于x∈R恒成立，且要取到等号，那么函数h（x）＝2|x-a|的图像应位于函数g（x）＝5-|x+1|的图像上方.首先作出g（x）＝5-|x+1|的图像，如图4所示，为使函数y＝h（x）的图像位于其上方且有公共点.注意两图像开口大小关系，我们容易得到y＝h（x）必过点（4，0）或（-6，0），代入解析式可求得a＝4或a＝-6.

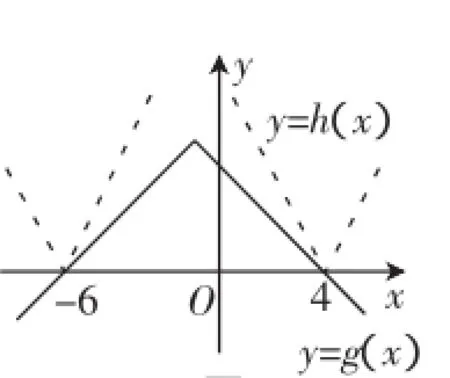
图4

四、结束语

在平时教学与解题过程中，若我们能加强解题后的反思，深度挖掘问题本质内涵，将会使我们对所学知识或所研究的问题有不一样的理解，从而促使我们从另一个视角去审视所学知识或所研究的问题，采取不一样的解决策略，这将极大地提高我们分析问题、解决问题的能力.F