他山之石可以攻玉——例谈构造法在不等式解题中的运用

☉江苏省张家港市崇真中学 王耀民

他山之石可以攻玉
——例谈构造法在不等式解题中的运用

☉江苏省张家港市崇真中学 王耀民

构造法是通过构造辅助量来解决数学问题的一种思维方法，是数学中一种富有创造性的思维方法.它根据数学问题的条件或结论的特征，以问题中的数学关系为“框架”，以问题中的数学元素为“元件”，通过深入分析问题的结构特征和内在规律，构造出新的数学对象或数学模型，使问题等价转化为与之有关的函数、方程和图形等，从而使问题得到解决.它常常表现出简洁、明快、精巧、新颖等特点，使数学解题突破常规，具有很强的创造性.本文以解决不等式问题为例，介绍几种常见的构造法.

一、构造方程证明不等式

某些不等式证明问题，可以根据它的条件或结论的特征构造一个一元二次方程，然后利用根的判别式来证明.

例1如果x，y，z均为实数，且x+y+z=a，x2+y2+z2=a2（a>0），求证：0≤x≤a，0≤y≤a，0≤z≤a（.北京市数学竞赛题）

证明：由已知的两个等式中消去x，得

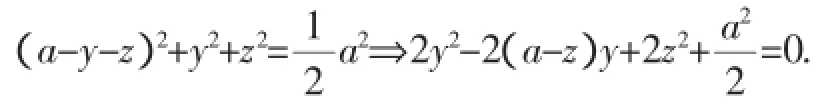
因为y∈R，

所以Δ=4（a-z）2-4（4z2+a2）≥0，

所以z（3z-2a）≤0.

点评：由于给出的已知条件是可以转化为两数之和与两数之积的关系式，这很容易使人想到根与系数的关系，从而联想到构造方程，利用判别式来解决.

二、构造函数证明不等式

根据欲证不等式结构的特点，引入一个适当的函数，运用函数的性质加以证明，通常根据所给式子的特点构造函数.

例2已知|a|＜1，|b|＜1，|c|＜1，求证：ab+bc+ac+1＞0.

证明：设f（x）＝（b+c）x+bc+1，由于|b|＜1，|c|＜1，

则f（1）＝bc+b+c+1＝（b+1）（c+1）＞0，f（-1）＝bc-b-c+ 1＝（b-1）（c-1）＞0.

由一次函数的性质知，f（x）在（-1，1）上恒大于0，而-1＜a＜1，故f（a）＝（b+c）a+bc+1＞0，即ab+bc+ca+1＞0.

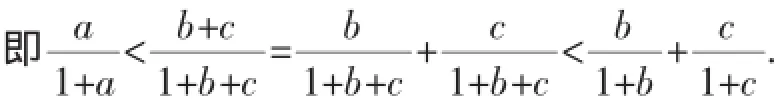
点评：构造函数证明不等式关键在于“转化”“构造”，根据式子的结构特点进行.如例2中a，b，c是对称的，也可构造f（x）＝（a+c）x+ac+1，证明f（b）＞0，还可构造f（x）＝（a+b）x+ab+1，证明f（c）＞0.例3中式子都具有的形式.

三、构造几何图形证明不等式

把欲证的不等式的数量关系所反映的几何背景找出来，然后根据几何图形性质证明不等式成立.

例4已知实数a，b满足a+b＝1，求证：（a+2）2+（b+2）2≥

证明：所证的不等式的左边可看作点（a，b）与点（-2，-2）间距离的平方，故可在平面直角坐标系中，构造点P（-2，-2），Q（a，b），其中Q是直线x+y＝1与两坐标轴的交点A，B连线段上的点，原不等式左边就是|PQ|2.

又△PAB为等腰三角形，所以PC⊥AB.故|PQ|≥|PC|，即|PQ|2≥|PC|2＝.

所以（a+2）2+（b+2）2≥.

点评：根据式子的特点和其几何背景，再用几何图形表示出来，根据几何图形的性质证明.

四、构造复数证明不等式

例5已知a，b，x，y∈｛正实数｝，且x2+y2＝1，求证：

证明：设z1＝ax+byi，z2＝bx+ayi，

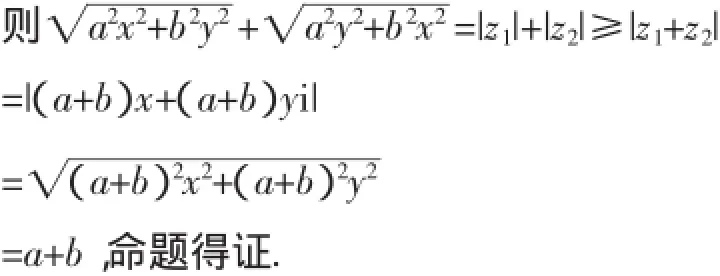
点评：复数是实数的延伸，一些难以解决的实数问题可构造转化为复数问题，虽然数的结构会变复杂，但常使问题简明化.正所谓“退一步海阔天空”.

五、构造定比分点证明不等式

由线段的定比分点定义可知，把P（x1），P（x），P（x2）看成数轴上的三个点，且，若λ＞0，则x∈［x，x］，12若λ＜0，则x∉［x1，x2］，反之结论也成立.利用这些结论证明与之形式特征相似的不等式，显得十分巧妙.

故可把P1（-1），P2（1）看成数轴上的三个点，且

因为|a|＜1，|b|＜1，所以1+a＞0，1+b＞0，1-a＞0，1-b＞0.

点评：构造定比分点必须要抓住式子的结构特点，构造与定比分点相似的式子，这点的要求比较高.

六、构造向量证明不等式

例7已知x，y是不等的正实数，求证（x4+y4）（x2+y2）＞（x3+y3）2.

证明：构造向量m＝（x2，y2），n＝（x，y），则

（x3+y3）2＝（m·n）2＝|m|2·|n|2cos2θ≤|m|2|n|2＝（x4+y4）（x2+ y2）.

因为x，y是不等的正实数，

所以（x3+y3）2≠（x4+y4）（x2+y2）.

所以（x4+y4）（x2+y2）＞（x3+y3）2.

点评：由于向量的模长、共线、垂直以及向量的数量积，用坐标表示后呈现出来的都是代数形式，因此，它给将代数问题转化为向量问题提供了方便，使我们可以将某些含有乘积之和或乘方之和的不等式，根据向量数量积坐标表达式的结构特征，构造向量加以证明.

七、构造数列证明不等式

由于数列是特殊的函数，当定义域是整数时，经常使用数列问题的处理方法.

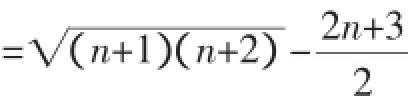
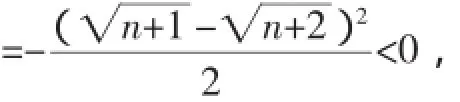
所以an+1-an＜0，

即an+1＜an＜an-1＜…＜a2＜a1＝■2-2＜0.

所以an＜0，即

点评：本例题的思路还是比较法，但由于作差后，得到一个变式，符号难以判断，但它是关于正整数的整式，可以联想到数列，利用数列的单调性获证.

八、构造辅助函数证明不等式

构造辅助函数的特点是构造出事物原本确实没有，根据需要与可能，通过类比、联想、改造、变通等方法组装成有利于解决问题的新事物.因此，数学中的“构造”既不神秘，也不难以捉摸，而是有章可循、有法可依，目的性和方向性都很强的一种操作技能、技巧.

例9已知m，n都是正整数，且1＜m＜n，证明：（1+m）n＞（1+n）m.

所以f（x）在［2，+∞）上严格递减.所以f（m）＞f（n），即

所以（1+m）n＞（1+n）m成立.

点评：两边取对数实属常用技能，但在这里却大显神威，可谓“四两拨千斤”.当不等式形式比较复杂时，可考虑先对不等式加以等价转化，然后根据情况构造辅助函数，故称此法为“转化构造法”，简称“转化法”.当不等式中出现指数式或超越式时，通常先对不等式两边取对数，然后构造辅助函数.

总之，用构造法证明不等式与用构造法求解其他的问题一样，能化繁为简、化难为易.构造法丰富的内涵对培养学生的思维能力有很大作用，因此这种方法在教学中应予以充分的重视.在面对一个个具体问题时，我们不应肓目地套用已有模式，而应根据题目，灵活变通，多管齐下，多法并用.Z