一道圆锥曲线试题结论的探究和应用

☉浙江省慈溪市杨贤江中学 周焱群

一道圆锥曲线试题结论的探究和应用

☉浙江省慈溪市杨贤江中学 周焱群

圆锥曲线包括椭圆、双曲线和抛物线，三者之间有许多共通的性质，而它们的这些共性也常常成为考试题目的命制背景和源泉.因此，在平时的解题教学中，教师一定要有意识地培养学生的题后反思的习惯、发展变式拓展的思维，逐渐提高学生解决问题的能力和良好的数学素养.下面我们以一道考试题目为例说明.

例1（2015年新课标全国卷Ⅱ）已知椭圆C：9x2+y2= m2（m>0），直线l不过原点O且不平行于坐标轴，l与C有两个交点A，B，线段AB的中点为M.

（Ⅰ）证明：直线OM的斜率与l的斜率的乘积为定值；

（Ⅱ）略.

证明：（Ⅰ）设直线l：y=kx+b（k≠0，b≠0），A（x1，y1），B（x2，y2），M（xM，yM），将y=kx+b代入椭圆方程，得（k2+ 9）x2+2kbx+b2-m2=0，由根与系数的关系，得x1+x2=，所以

一、由特殊到一般，探究结论真伪

问题的探究并没有因解题结束而终止，这个结论对于一个一般的椭圆是否成立呢？

证明：设A（x1，y1），B（x2，y2），M（xM，yM）.将A（x1，y1），B（x2，y2）代入

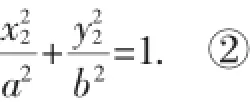
定值为短半轴的平方除以长半轴的平方的相反数.

若椭圆的焦点在y轴上呢？还是这个定值吗？

证明：设A（x1，y1），B（x2，y2），M（xM，yM）.

将A（x1，y1），B（x2，y2）代入

所以kOM·kl=-为定值，定值为长半轴的平方除以短半轴的平方的相反数.

二、横向拓展到双曲线

探究已知双曲线C：（a>0，b>0），直线l不过原点O且不平行于坐标轴，l与C有两个交点A，B，线段AB的中点为M，则直线OM的斜率与l的斜率的乘积为定值，即定值为实半轴的平方除以虚半轴的平方.

（仿照探究2的证明可以得到此结论，证明略）.

三、横向拓展到抛物线

探究5已知抛物线C：y2=2px（p>0），直线l不过原点O且不平行于坐标轴，l与C有两个交点A，B，线段AB的中点为M（x0，y0），则直线OM的斜率与l的斜率的乘积为定值

Atrophic mucosa with intestinal metaplasia in differentiated gastric cancer and undifferentiated cancer of the gastric fundic gland mucosa are well-known examples of the relationship between gastric cancer and the background mucosa[37].

证明：设A（x1，y1），B（x2，y2）.将A（x1，y1），B（x2，y2）代入y2=2px，得

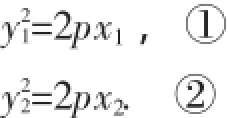
由①-②，得（y1-y2）（y1+y2）=2p（x1-x2），即

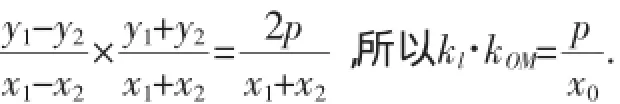
针对抛物线的焦点在x轴负半轴及焦点在y轴上时定值情形，请同学们自行探究.此处略.

四、探究落实应用

探究的目的是为了应用其解题，下面简举几例.

（Ⅰ）求椭圆E的方程；

（Ⅱ）求△PMN的面积取最大时直线l的方程.

设MN的方程为y=-（m≠0），代入椭圆=1并整理得3x2-3mx+m2-3=0.由Δ=（3m）2-4×3（m2-3）= 3（12-m2）>0，解得m∈（-2，0）∪（0，2）.

又因为xM+xN=m，xM·xN=

例4设F为抛物线C：y2=4x的焦点，过点P（-1，0）的直线l交抛物线C于A，B两点，点Q为线段AB的中点.若|FQ|=2，则直线l的斜率等于______.

解析：设点Q的坐标为（x0，y0），则由探究5可得kl·

由|FQ|=2，得（x0-1）2+=4.②

由①②得x0=1，y0=±2，代入

综上所述，利用探究所得结论对以上各例的解答，使原本复杂的解题过程得以简化，优化了解题思维.虽然在解答主观题直接应用此结论略有不妥，但可起到明确解题思路、指引解题方向的作用，而且可以提高解题速度、效率，是值得我们学习思考的.Z