解法应以自然、简捷、通用为上*——高三复习课“一题六解”教后反思

☉福建省厦门大学附属实验中学 邱云

解法应以自然、简捷、通用为上*
——高三复习课“一题六解”教后反思

☉福建省厦门大学附属实验中学 邱云

做题、讲题是高三复习课的主旋律.题海无涯，解法不定；学时有限，积沙成塔.试题讲评课的效率与学生解题能力的提升息息相关.教学中，常听老师感叹、抱怨：“做过讲过的问题学生还是不会，讲过两三种方法还是没掌握……”高三复习课讲评试题，如何把握好“传道、授业、解惑”的度？如何让学生在听讲中能真正温故知新、学有所长？如何处理好构建知识网络与提升数学能力的关系？如何让学生在疲惫与压力中保持课堂学习的持久热情？……都是需要老师思考研究的问题.

一、现状

高三复习课中，对学生完成得不理想的考题、作业、练习通常有以下讲评方式：①提供答案让学生自己核对；②就题论题，讲一种师生最熟悉、最通用的方法；③一题多变，讲完一种解法再做几道变式练习加深印象；④一题多解，把老师能想到、能收集的解法一网打尽；⑤选择性讲解，着重介绍学生能想到、易掌握的若干解法.据了解，高三数学老师普遍觉得复习时间紧、内容多、压力大，总觉得每节课时间不够用，但讲题时解法大多还是求多求全，采用方式③④者居多.无论采用哪种讲授方式，老师讲学生听、“我的课堂我作主”是高三试题讲评课的一种常态.这一常态下，学生疲于听讲、被动“矫正”，很少有思维交流与碰撞；每次测试，做过的题型频频失分、讲过的方法思路错乱也成“常态”，老师们也总惆怅于复习效果不佳.

二、课例

1.高三复习测试题

题目（2014年湖北高考理科卷）已知F1、F2是椭圆和双曲线的公共焦点，P是它们的一个公共点，且，则椭圆和双曲线的离心率的倒数之和的最大值为（）

据笔者所教学生答题情况统计，会做的同学很少，该题难度系数为0.24.

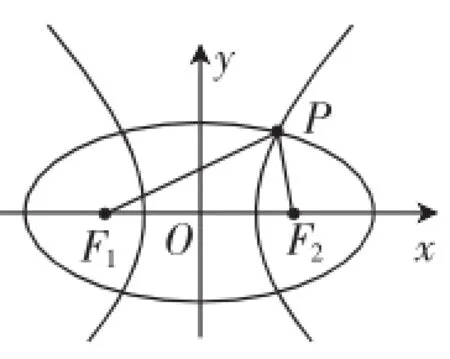
图1

2.学生思路

如图1，设椭圆的长半轴为a1、离心率为e1，双曲线的实半轴为a2、离心率为e2，半焦距为c，|PF1|=r1，=r，则r+r=2a，r-r=2a，+2121122由余弦定理得4c2=+-r1r2，即4c2=+.大多数基础较好的同学思路止步于此，有些往前走了一步，得到（*）.

3.课堂讲评

这是一道背景熟悉、知识交汇、方法多样、思想丰富的圆锥曲线综合题.学生普遍“束手就擒”，望题兴叹.于是笔者想花足时间将此题讲清讲透，预设了法1、法2、法5、法6，以期帮助学生解开疑团，让其体会知识间深刻、巧妙的内在联系，见识“小题大做”的精彩.

因对椭圆的参数方程不熟悉，加之将（*）式看作椭圆方程需要较强的“式感”与整体观察能力，极少同学想到此法.听完老师分析，并没产生预期的良好共鸣.

法2：（利用柯西不等式）（两个数学功底较好的同学迫不及待迫地举手回答，这正是老师想讲的第二种方法）

因为我们同学没有选考不等式，还是一年前上过新课，柯西不等式已基本忘记.原本很常规的构造，在学生看来也觉得很复杂.老师追问：还有什么方法吗？生1站起来讲述了方法3.

在考场，很多同学也往这个方向想，试图列出一个函数求最解，但没能构造出关于的二次函数.一位当初有此想法但没解对的生2补充道：先求的倒数更简单些，即求的最值.生1、生2的解法得到广大同学的点头赞许.

正当老师准备讲解法5、法6时，平时机灵、沉默的生3说：老师不用那么复杂，用几何法很简单.此时让笔者有些诧异，因为自己从没想过有什么几何法可用，于是把生3请上台讲解他的妙法4.

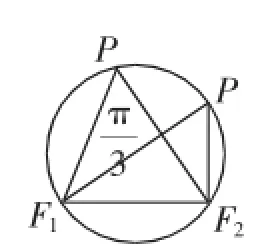
图2

生3数形结合、简单直观的解法博得热烈掌声，但“圆”的借用让人觉得有点玄乎.

生4激动地补充道：“老师不用画圆，用正弦定理解释即可.”如图1，在，所以当取得最大值

正弦定理，一步到位！全体同学如同拨云见日，豁然开朗，纷纷惊叹于生4的“伟大发现”.生3姓方，生4姓王，笔者即兴将法4命名为“方法+王法=巧用正弦定理”.同学们会心一笑，“方、王”心生自豪.如此灵活、简洁又通俗的方法竟然老师没想到，赞赏之余顿感惭愧.

在同学们兴致勃勃中，笔者又介绍了课前预设的法5、法6，学生反应平平.

法5：（构造均值不等式）因为（x+y）2=x2+y2+2xy=x2+

法6：（借用判别式）令x+y=t，代入x2+3y2=4，得4y2-

三、调查

讲评前，笔者问了一些同学：“关于这道题你最想听什么？”答“：”怎么用？除椭圆和双曲线的定义及余弦定理外，还要用什么知识？变量太多，怎么构造关于离心率的函数？有没有简单好用的方法？

考试时全班只有个别学生会解此题，用的都是法3或法2.笔者期待，经过老师“彻底讲解”，学生普遍能掌握二至三种方法，再解此类题，正确率应该大幅提升.为了了解学生听讲后真实的内化吸收情况，讲评2天后，笔者对考试时不会解此题的10位同学进行了调查.结果出乎意料，效果事与愿违：有8位同学能记住图2，其中7位同学能基本复述法4；有6位同学能想起法3，他们在考场大都卡在了式子：的变式处理上；只有1位同学能回忆起法1、法2；没有同学会用法5、法6解题.从调查结果看，学解题的第一步——“记忆模仿”的目标还未达成，更别说“变式练习、自发领悟、自觉分析”了.

笔者又询问了同备课组的5位老师当时是怎么解这道题的.老师们都用了法1和法2.查阅各种教辅资料，提供的参考答案也都是用三角换元或柯西不等式.可见，由于老师对“椭圆的参数方程”及“柯西不等式”比较熟悉，故不约而同地形成定势思维，运用了一致的解法.

四、反思

1.顺应学生思维，探求自然解法

数学是自然的，数学解题也贵在自然.解法的生成应该从学生已有的知识经验和思考基础出发，立足大多数学生的思维受阻点，跟着学生的思路走，努力寻求自然的解法，这才是最真实和最宝贵的.如果解题分析以老师的想法为中心，一味地醉心于自己的多种解法，则易形成低效讲授，师者滔滔不绝的讲解也许就是一场孤芳自赏的独角戏.

试题讲解中，教师应以生为本，顺应学生思维，多想学生之所难，帮助学生跨越思维障碍，让学生的思维自然流淌、解法水到渠成.本课例中，生1、生2的“构造二次函数”法虽然从代数形式上看起来比较复杂，但得到广大同学的欢迎认可，是因为它源于大多数人的自然思路.有“平方”、“最值”出现，凭“经验题感”，“构造相应的二次函数求解”是学生熟悉且常用的解题策略.但是要以整体的眼观把“”看作函数自变量，又成了众生的思维障碍.这一“最近发展区”一旦突破，老师眼中的“复杂形式”对学生来说已不是难事，于是在学生眼中貌似复杂的法3比老师惯用的法1、法2更高明.实践证明“构造二次函数法”因为自然，所以有效，其习得过程也是一次完善思维、体验成功的成长过程.

因此，解题教学因基于学生的认知，源于学生的思路，通过启发引导，让其自己思考，自己发现，形成自己的理解.试题分析中，让学生说出心中的困惑，使学生的思维得以延伸，最终“顺藤摸瓜”帮助学生探求出自己解决问题的自然想法，从而让解题受挫者体验成功解决问题的快乐，激发其继续学习的兴趣和信心.这样，学生在学习与解题的过程中，掌握数学知识的同时学会数学地思考，在思考中提升思维能力、丰富数学素养.

2.让位学生思考，寻求最美解答

数学世界的魅力就在于人们无止境地追求其简捷之美，进而享受数学之美.简单性是数学方法美的主要标志，正如爱因斯坦感叹：“美，本质上终究是简单性.”解题时最美解答应当是充分发掘题目信息，灵活运用思想方法，推理表达自然清晰，让人感觉简捷明快、通俗易懂，而非突兀的“神来之笔”.

学生是天生的舞者，舞台有多大，他的思路就有多宽.课堂是学生发现美、创造美、享受美的舞台.苏霍姆林斯基说过：“在学生的内心深处有一种根深蒂固的需要，就是希望自己是一个发现者、研究者、探索者.”因此，课堂教学中要给学生的思维绽放留足时间与空间，为学生的奇思妙想搭建自由的舞台，试题讲评也不例外.

课例中，生2对“构造二次函数法”的改进，使得法3更平易近人；方同学将求“”转化为先求“的创举给了王同学灵感，使化归与转化及数形结合的思想之美活灵活现，让深得人心的最美解答——“巧用正弦定理”应运而生，原本艰涩的试题显得熠熠生辉，原本平静的课堂充满生机与活力，教师在惭愧中也感受到教学相长的课堂幸福.倘若教师缺乏“让位”与“放手”意识，只满足于自己熟悉的四种方法的“表演”，匆匆而过便讲评下一道题，那错过的不仅是最美解答，更有学生“再创造”的激情与冲动.

数学家高斯说：“去寻求一种最美和最简捷的证明，乃是吸引我研究的主要动力.”美是真的光辉，依靠这种光辉可以照亮认识数学真理的道路，并给探求者一种认识道路的内驱力.高三学生正值精力充沛、思维活跃、激情燃烧的青春岁月，课堂应当是涌动着的生命，而非沉闷、疲惫的被动状态.教师要改变以往试题讲评中“满堂灌”、“一言堂”等老套方式，要勇敢地“让位”，勇敢地把课堂还给学生，鼓励生生之间、师生之间踊跃地思维交流与表达.只有这样，学生才能于深思顿悟间灵机一动，催生出令人茅塞顿开的最美解答；也只有这样，才能激励学生不断迸发出智慧的火花，想出更多更美的方法，在解题能力上达到“青出于蓝而胜于蓝”的佳境.

3.注重通性通法，讲求详略得当

波利亚在“怎样解题表”中阐述了解题者在面对问题时寻求突破的一般思路.一般思路就是在解决具有相同性质的数学问题时常用的数学思想与方法，即通性通法.《2016年全国统一考试大纲的说明》在考查要求中明确提出：“考查时注重通性通法，淡化特殊技巧，有效地检测考生对中学数学知识中所蕴含的数学思想和方法的掌握程度.”

佳肴虽好，若不顾消化吸收能力，贪吃无度，则影响健康，适得其反.解法虽多，若不顾学生认知实际，全盘传授，则一厢情愿，广种薄收.课例中的“最值问题”，已知，运用余弦、正弦定理探寻三角形的边角关系；构造与所求问题有关的函数表达式或基本不等式是“常法”.其中蕴含的函数、转化及数形结合思想，构造、换元及整体观察的数学方法便是解决“最值问题”的通性通法.试题讲评中，法1、法3、法4可重点详细讲解.而“构造均值不等式与柯西不等式”及“借用判别式”技巧性强、思维难度大，平时又少见少用，属“偏法”，可让学有余力的同学课后选择性吸收，不必在课堂“灌输”，尤其是法5、法6.解题教学中，教师不应做解法的“奴隶”，要做学生的“知己”.盲目地授人多鱼，不如授人一渔.

试题讲评旨在帮助学生突破思维障碍、深化知识理解、优化解题思路、提升思维能力，应站在帮助学生学会解题的角度，构建高效课堂，激活学生智慧，增强复习实效；解法传授应以自然、简单、通用为上，择善而从，而非多多益善，以免广种薄收.

1.郑良.探析命题特点明晰教学方向——2015年高考数学全国卷试题评析及高三复习建议［J］.中学数学教学参考（上），2015（12）.

2.罗增儒.中学数学解题的理论与实践［M］.南宁：广西教育出版社，2015.

3.蔡小冲.让学生的个性品质在难题突破中得到升华——一道高考数学压轴题的突破感悟［J］.中学数学（上），2014（5）.F

*2013年教育部人文社会科学研究规划基金项目《数学教师基于教学的学科知识水平发展研究》（课题编号：13YJA880043），本文是该项目的部分研究成果.