三评三讲一变式——提高试卷讲评课效果之我见

☉广州市真光中学 金明

三评三讲一变式
——提高试卷讲评课效果之我见

☉广州市真光中学 金明

一、问题提出

试卷讲评课是高三数学教学的重要课型.但试卷讲评课的效果如何呢？值得探讨.教学中常常见到这样的现象：为了追求高效率，教师一节课讲十几题，甚至更多.教师在讲台上一题一题的讲，学生在下面默默的听；教师讲得苦，学生听得累.课堂教学沉闷，教学效果不好.究其原因不是学生不想学，而是教师对学生存在的问题分析不够，没有找准学生的困惑点；教师对学生思维的闪光点关注不够，没有将其深化、拓展；教师对学生存在的问题如何解决重视不够，没有设计有效的变式练习、查了漏洞但补救措施不力.长此下去，学生对讲评课兴趣不浓，因而效果不好.怎样提高讲评课的效果呢？笔者通过一道月考题的讲评实践，谈谈自己的看法.

二、课堂教学实践

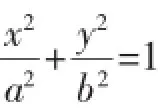
问题：平面直角坐标系xOy中，已知椭圆C：（a>0，b>0）的离心率为，左、右焦点分别是.以 F1为圆心3为半径的圆与以F2为圆心1为半径的圆相交，且交点在椭圆C上.

（Ⅰ）求椭圆C的方程；

（2）求△ABQ面积的最大值.

本题为我校高三12月月考题，选自2015年高考山东卷.它是一道圆锥曲线综合题，考查了椭圆的定义、方程、直线与圆锥曲线的位置、求最值等知识；考查了数形结合、分类讨论、转化化归等数学思想方法.通过该题的考试，发现了学生在很多知识、方法方面的漏洞，也发现了学生思维的闪光点.讲评前笔者对学生的答卷进行了认真的分析与准备.讲评时采取先暴露学生的问题，让学生发现问题，再师生合作共同探讨帮助解决问题.以下是教学实录片断：

1.评对错，找困惑点与着力点，讲概念

试卷讲评关键是要找准学生的问题：是知识上存在缺陷还是方法上存在问题？是思维能力达不到还是别的什么问题？找准了问题再思考从哪些方面着力，突破学生的思维障碍.

教学片断一：第（1）问的分析与探讨.

教师先投影学生1的解法：设P（x0，y0），F1（-c，0），F2（c，0）.

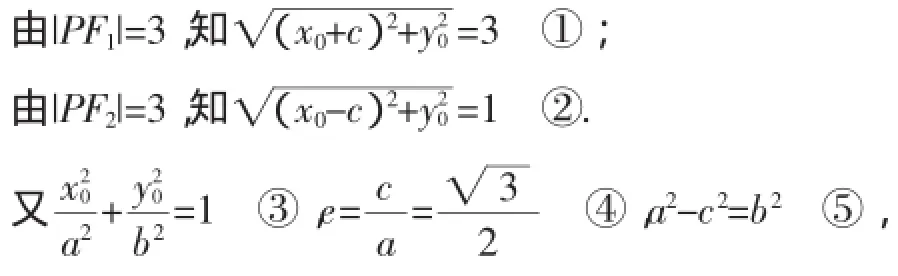
解得a2=……做不下去了.

师：请同学们思考一下生1的做法，看有什么问题？

生2：这位同学每一个式子都是对的，就是参数太多，消不了，做不出来.

生4：这道题哪里需要这么繁，只需理解：以F1为圆心3为半径的圆与以F2为圆心1为半径的圆相交，且交点在椭圆C上.由椭圆定义可知|PF1|+|PF2|＝2a＝4，口算就能得出结论.

师：大家的讨论都有道理.看来理解题意很重要，画出图形可帮助我们理解题意.用定义解题是解决圆锥曲线问题的重要方法.问题是怎么想到要用定义？何时用定义，是同学们学习的薄弱环节.请同学们思考以下变式题：

变式题1：已知圆M：（x+1）2+y2＝1，圆N：（x-1）2+y2＝0，动圆P与圆M外切并与圆N内切，圆心P的轨迹为曲线C.求C的方程.

A.|MO|-|MT|＞b-aB.|MO|-|MT|＜b-a

C.|MO|-|MT|＝b-aD.|MO|-|MT|与b-a无关

教学感悟：教师首先投影学生的解题过程，让学生分析、讨论，找出存在的问题与不足，并让学生帮忙解决问题.问题从学生中来，解决措施也来自学生，更贴近学生的实际，吸引更多的学生参与到教学中来.找到了问题，教师引导学生复习相关的核心概念，并设计了2个变式题让学生思考练习，强化巩固所学概念，解决难点.

2.评差异，找重点与闪光点，讲方法

所谓评差异就是展示学生不同的解题思路，并进行比较分析，找出优缺点，找学生解题中的闪光点；然后确定应该突破的重点与难点，讲此题用到的基本方法.

教学片断二：第（Ⅱ）题第（1）问的分析与探讨.

教师先投影学生5、学生6的解法：

设P（x1，y1），Q（x2，y2），则有

设P（x1，y1），Q（x2，y2），则直线OP的方程为y＝

师：请同学们分析一下生5与生6的做法，有无问题，能否做下去？

生7：我觉得生5的做法没问题，每个式子都是对的，就是参数太多，运算量太大.至于怎么做下去，我没想好.

生8：我的做法与生5的差不多，我的解法如下：设OP的方程为y＝kx，由可求P点坐标，得.同理，由可求Q点坐标，得

（生众非常激动，不自觉地为生8鼓掌.）

生9：我觉得生8的做法有点小问题，他没考虑直线OP的斜率不存在的情况，所以还要将这种特殊情况写出来.

生10：生6的解法也可进行下去，她还有个条件没用：点P（x1，y）1在椭圆C：所以有

师：刚才几位同学分析得非常好.生5、生6的思路是对的，也能做下去，但在考场上出现了问题，说明了此方法不够简洁.究其原因是参数设得太多，影响了顺利消参.为此，解题时参数不要设得太多.另外，设点斜式时要考虑特殊情况（即斜率不存在的情况），本题中从特殊情况出发可很快得出结论，还有别的解法吗？

生11：设P（x，kx），Q（x，kx）.由点P在椭圆C上知+

1122.由点Q在椭圆E上知，得

生12：我是用参数方程解的.设P（2cosα，sinα），则Q（4cos（α+π），2sin（α+π））.

师：非常不错，这些同学的解法非常优秀.生11的解法与生8的解法类似，但更简洁.生12的解法用到椭圆的参数方程，他关注到P、Q在同一直线上，设角度分别为α，π+α，解法更加快捷方便.生13化未知为已知，设＝λ，将比值问题转化为向量问题＝-λ，方法独到，非常好.经过同学们的合作，我们找到此题的6种解法.

教学感悟：教学过程中，教师要有意识地创设问题情境，投影展示生5、生6不成功的解法，以此创设问题情境，激发学生思考.让学生思考、探究、交流，留有充裕的时间让学生质疑问难；引导学生讨论，畅所欲言，积极发表意见.学生的思维在交流中得到了碰撞，大大地激发了学生的求知欲望和探索兴趣；经过教师的追问和学生的积极探究，课堂生成了6种解法，沟通了知识之间的联系，拓展了学生思维空间.从以上教学片断，不难发现，学生掌握了探究知识的主动权，教师几乎没有讲解，只是预设问题，适时追问，极力营造生动和谐的课堂氛围，宽松的思维环境，最大化地激发了学生学习的积极性，学生由被动接受变为主动思考、主动探究、主动解决问题，教师只是引导学生归纳、提炼解题的基本方法.

3.评核心，找难点与回避点，讲思想方法

评核心就是评此题用到的核心概念、核心方法.找到学生解题时遇到的难点，从而确定不同层次的学生（优生、中等生、后进生）应当在哪些方面努力，哪些方面可以暂时回避.

教学片断三：第（Ⅱ）题第（2）问的分析与探讨.

教师先投影学生14的解法：设A（x1，y1），B（x2，y2），将y＝kx+m代入椭圆E的方程，可得（1+4k2）x2+8kmx+4m2-16＝0，由Δ＞0可得m2＜4+16k2①.

又x1+x2＝故|AB|＝

设Q（x0，y0），由Q到直线AB的距离为

师：请同学们分析一下生14的解法有什么问题，如何改正.

生15：还是参数太多，无法消参.

生16：参数k、m是题中所给，是必要的.但多出的参数x0、y0不好处理.

师：上面两位同学点出了关键，怎么求解呢？能联想到第（1）问吗？

生17：哦，先求△AOB的面积，再利用S△QAB＝3S△OAB即可，这样就不会有参数x0、y0了.

生18：我也是先求△AOB的面积，但是做到S△AOB＝时就不知该如何求最值了.

生19：有两个参数k、m，解题方法通常是换元成一个参数或者用基本不等式.先变形为换元设t＝，这样就容易了，当然要注意求t的范围.

师：经过同学们的讨论我们发现这一问的难点是转化.将不易解决的问题（如求S△QAB）转化为易解决的问题（如求△AOB的面积），关键是要发掘第（1）问的结论，还有一个是要学会转化.转化思想是数学的核心与灵魂.

教学感悟：教学过程中，教师投影展示生14不成功的解法，引导学生交流，让学生发表看法，引出学生的疑问与困惑，然后导出核心思想：转化与化归的思想；核心方法：直线与圆锥曲线联立，韦达定理，设而不求；换元法，基本不等式求最值等.对不同层次学生提出不同的要求，如所有学生应掌握：直线与圆锥曲线联立，韦达定理，设而不求；中等生应领悟基本不等式求最值；优生要熟练掌握以上各种方法.

4.变式训练，解决存在问题

通过此题的解答，发现了学生在基础知识与能力方面存在的问题.既然有问题，就要及时解决，这样学生就有兴趣上讲评课了.同时设计针对性的练习，有助于学生巩固基础，提高能力.为此，本节课笔者设计的变式练习如下：

（1）△ABC的顶点A（-5，0），B（5，0），△ABC的内切圆圆心在直线x＝3上，则顶点C的轨迹方程是__________.

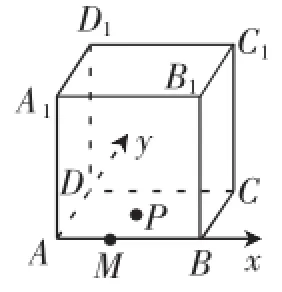
图1

（2）如图1所示，正方体ABCD—A1B1C1D1的棱长为1，点M在AB上，且AM＝AB，点P在平面ABCD上，且动点P到直线A1D1的距离的平方与点P到点M的距离的平方差为1，在平面直角坐标系xAy中，动点P的轨迹方程是____________.

（4）已知实数x，y满足方程x2+y2-2x+4y=0，则x-2y的最大值是________.

（6）如图2，已知两条抛物线E1：y2=2p1x（p1>0）和E2：y2=2p2x（p2>0），过原点O的两条直线l1和l2，l1与E1、E2分别交于A1、A2两点，l2与E1、E2分别交于B1、B2两点.

证明：A1B1∥A2B2.

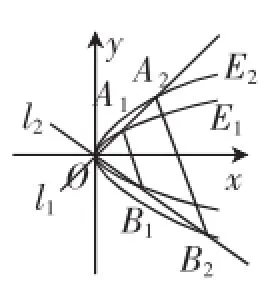
图2

①求椭圆C的方程；

②当过点P（4，1）的动直线l与椭圆C相交于两不同点A、B时，在线段AB上取点Q，满足证明：点Q总在某定直线上

设计意图：（1）、（2）两题是用定义解题，第（3）题是用三角换元或数形结合转化为切线问题解题，第（4）题是用三角换元或化未知为已知转化为直线与圆有交点问题，第（5）题是解决如何用基本不等式求最值问题，第（6）题是解决如何设参数问题，第（7）题是探讨如何将比例式化为向量式和如何消参等问题.以上问题的设计是针对学生在解题时出现的问题（有知识层面也有方法层面）而设计的，目的是巩固学生的基础与提升学生的能力，选题针对性强，为学生的进一步探索提供了素材.

三、上好试卷讲评课的思考

当前，讲评课教学效率不高，学生兴趣不浓是普遍现象，可能很大程度是我们老师贪多求快，对学生不放心；企图课堂上多讲几道题，以为学生就会多领会一点，多掌握一些；对学生的需求关注不够，对学生的思维能力的培养研究不够，对学生的试卷分析不到位.

1.上好试卷讲评课，要做好研究、交流剖析问题、拓展思维空间

上好讲评课首先要认真分析学生的试卷，善于发现存在的问题与思维的闪光点.课堂上教师要展示学生的解法，让学生讨论，让学生辩析，找出存在的问题与闪光点，并让学生讨论解决错误的方法；尽可能多地展示来自学生的不同解法，拓展学生的思维空间.如本节课教师研究了学生的解法，都是从学生解题过程的剖析入手，让学生讨论存在的问题与思维的闪光点，让学生探索此题的正确解法.教师要善于总结与引导，帮助学生理清解题思路与解题方法，使思路与方法系统化、网络化.试卷讲评课如何吸引学生使学生愿听、愿想、愿探究，关键是要研究学生与试题，课堂上通过对重点题的研究，能辐射到多种思想方法或能起到构建知识框架的作用，或能揭示一般性的解题方法，从而达到教学效益的最大化.

2.上好试卷讲评课，要做好查漏补缺、一题多思、一题多变等工作

对学生的不足之处，要设计变式题补救，不能放任自由.有的变式题在课堂上完成，有的要作为课后作业.变式题的设计要有针对性，针对学生存在的问题，使学生通过变式题的练习与探索，能查漏补缺、拓展思维、提升能力.如本节课设计的7道变式题就是根据学生存在的问题而设计的，针对性强.同时通过以上问题的变式探究，使学生在思考、比较、归纳的过程中，理清基础知识，构建知识网络，形成思维能力.

1.金明，叶东芳.数学教学要重视知识的形成过程［J］.中学数学（上），2015（7）.

2.李建潮，宋卫成.摭探数列前n项和的适当放缩［J］.中学数学教学参考（上），2010（10）.

3.金明，贺育林.要短效高分，还是长效能力［J］.数学通讯，2015（5）.

4.徐勇.在错误中寻找学生的最近发展区［J］.中学数学教学参考（上），2010（7）.

5.李真福.对一道高考模拟题的思考［J］.中学数学（上），2011（7）.F