电磁矢量阵列的四元数Toeplitz矩阵重构算法

张远芳，李会勇，谢菊兰

(电子科技大学 电子工程学院, 成都 611731)

·信号处理·

电磁矢量阵列的四元数Toeplitz矩阵重构算法

张远芳，李会勇，谢菊兰

(电子科技大学 电子工程学院, 成都 611731)

对于电磁矢量阵列的相干信源波达方向估计，针对空间平滑算法解相干时减少阵列有效孔径的问题，提出了一种四元数Toeplitz矩阵重构算法。首先，根据四元数的正交特性建立了信号接收模型，很好地保持了电磁矢量阵列的阵元输出信号两分量间的正交性，同时保证了波达方向角信息和极化信息都能包含在重构矩阵中；然后，在阵列各阵元接收数据与参考阵元接收数据的相关函数基础上，构成Hermitian Toeplitz矩阵，从而实现解相干。该算法与空间平滑算法相比增加了相干信源估计个数，且在低信噪比和入射角度接近时具有更好的估计性能，通过仿真实验得到了验证。

电磁矢量阵列；相干；四元数；Toeplitz矩阵

0 引 言

电磁矢量阵列能够同时获得波达方向信息和极化信息，较传统标量阵列具有诸多优良的性能[1-2]。波达方向(DOA)估计是阵列信号处理的研究热点，传统的基于子空间类算法，如多重信号分类(MUSIC)算法、旋转不变子空间(ESPRIT)算法，对于非相干信源具有很好的估计性能[3-4]。由于空间中复杂电磁干扰和多径效应使得信号源产生相干，导致接收信号自相关矩阵秩亏，子空间类DOA估计算法失效。

空间平滑算法[5-7]是一种常用的电磁矢量阵列解相干算法，但是此类算法是以减少阵列有效孔径为代价来解相干的。文献[8-9]提出了极化平滑算法以及一系列在此基础上的改进算法，虽然没有减少阵列有效孔径，但是最多只能估计六个信号源。文献[10-11]提出了基于四元数的空间平滑解相干算法，在估计性能上有所提高，但是解相干信源个数仍然有所限制。文献[12]提出了电磁矢量传感器阵列的矩阵重构算法，该算法只是将接收数据的自相关矩阵的第一行元素进行矩阵重构，并未将信息全部用到。本文提出了一种基于四元数的Toeplitz矩阵重构算法。

1 四元数信号模型

如图1所示的均匀线阵由M个沿y轴排列的阵元构成，阵元间距为d。其中每个阵元由两正交的电偶极子对构成，两正交的电偶极子分别沿平行于x轴和y轴方向放置。两正交分量的极化导向矢量为

(1)

式中：θ∈[-π/2, π/2)为入射信号俯仰角；φ∈[0,2π)为入射信号方位角；γ∈[0,π/2)为极化幅角；η∈[-π,π)为极化相位差。

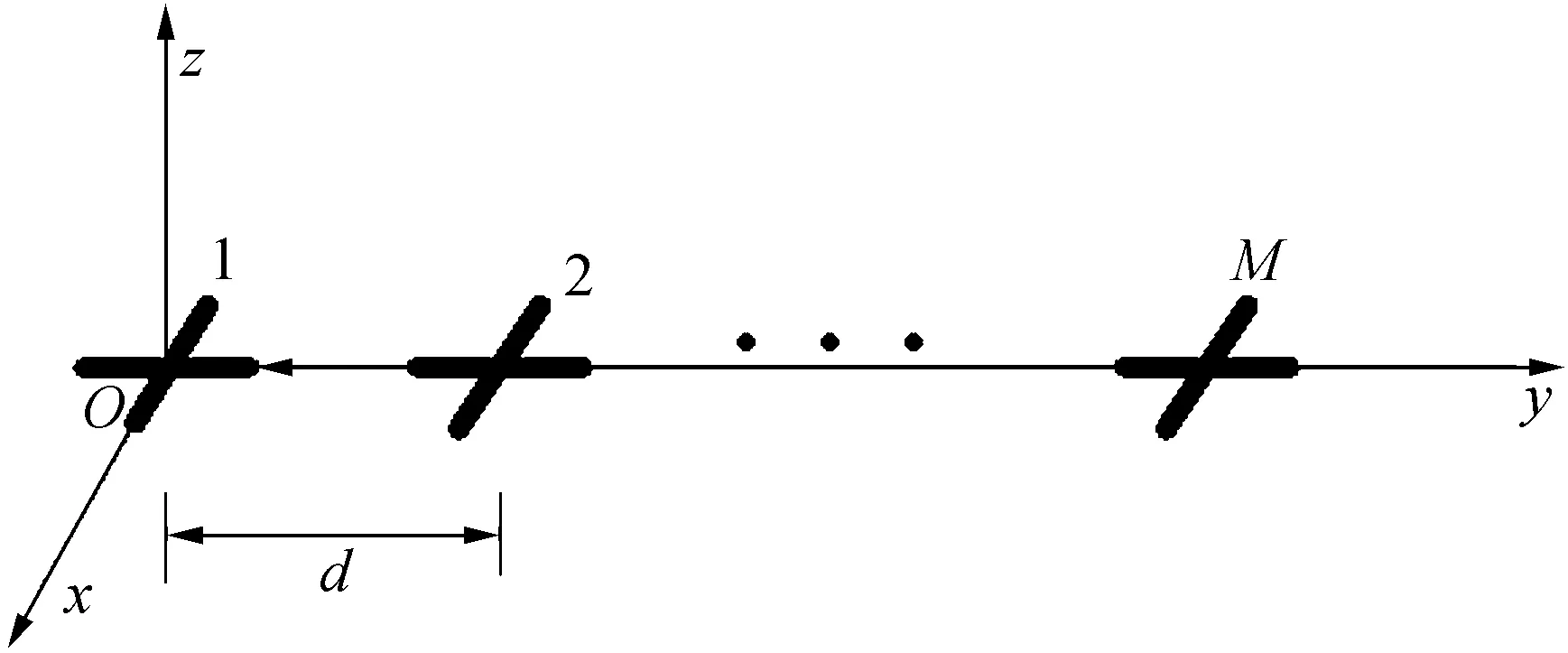
图1 极化敏感阵列结构图

一个信号s(t)入射到均匀线性阵列，为方便分析，固定φ=π/2，则接收信号的两分量xmx(t)和xmy(t)可以表示为

xmx(t)=-cosγs(t)

(2)

xmy(t)=cosθsinγejηs(t)

(3)

用四元数来表示接收信号的两分量，则可以写成

(-cosγ+icosθsinγejη)s(t)=

P(θ,γ,η)s(t)

(4)

式中：P(θ,γ,η)为一个四元数。对于整个阵列的接收信号可以表示为

x(t)=P(θ,γ,η)s(t)as(θ)

(5)

式中：as=[1,ejφ,…,ej(M-1)φ]T为空间导向矢量；φ=2πdsinθ/λ。

假设空间中有K个信号入射到阵列，阵列接收数据可以表示为

Ds(t)+N(t)

(6)

式中：D为阵列四元数流形矩阵；s(t)=[s1(t),s2(t),…,sK(t)]T为入射信号；N(t)为零均值，方差为σ2的高斯白噪声。D表示为

(7)

接收数据的自相关矩阵表示为

Rx=E[X(t)X◁(t)]=DRsD◁+σ2I

(8)

式中：符号{◁}表示四元数共轭转置；Rs表示入射信号自相关矩阵。由于入射信号相干使得Rs不再是一个满秩的矩阵，一般的参数估计方法都不再适用，接下来将进行解相干处理以恢复接收信号自相关矩阵的秩。

2 四元数Toeplizt矩阵重构算法

第m个阵元的接收数据可以表示为

xm(t)=xmx(t)+ixmy(t)=

D(m)s(t)+nm(t)

(9)

式中：D(m)表示D的第m行所有元素。

第一个阵元的接收数据可以表示为

x1(t)=D(1)s(t)+n1(t)

(10)

以第一个阵元为参考阵元，定义相关函数为

D(1)E[s(t)s◁(t)]D◁(m)+σ2δ(m-1)=

D(1)RsD◁(m)+σ2δ(m-1)

(11)

将m从1到M的相关函数进行排序，得到矢量为[r(0),r(1),…,r(M-1)]，将式(10)代入矢量可以得到

[r(0),r(1),…,r(M-1)]=D(1)Rs[D◁(1),

D◁(2),…,D◁(M)]+[σ2,0,…,0]

(12)

构造如下形式的矩阵

(13)

可以看出，矩阵包含所有的信号源入射角信息和极化信息，由式(11)可以得到r(m-1)=r*(1-m)，证明如下

r(m-1)=D(1)RsD◁(m)+σ2δ(m-1)=

σ2δ(m-1)

(14)

r(1-m)=D(m)RsD◁(1)+σ2δ(m-1)=

σ2δ(m-1)

(15)

由式(14)和式(15)可得

r(m-1)

(16)

因此RT为Hermitian Toeplitz 矩阵，从而实现了解相干[13]。

对重构矩阵RT进行特征值分解得到信号子空间和噪声子空间，利用四元数MUSIC算法[10]来完成参数估计，谱峰极大值处对应的角度即为信号入射角度。

3 算法仿真与分析

3.1 仿真实验1

四元数Toeplitz矩阵重构算法和四元数空间平滑算法解相干信源个数的对比。

假设阵元数M=8，阵元间距d=λ/2，噪声为高斯白噪声，其功率为1，快拍数为512，信噪比为10 dB。相干信号个数K=6，其来波方向角分别为-60°、-40°、-20°、0°、30°、60°，极化参数(γ1,η1)=(10°,50°)、(γ2,η2)=(20°,30°)、(γ3,η3)=(10°,15°)、(γ4,η4)=(40°,60°)、(γ5,η5)=(30°,40°)、(γ6,η6)=(50°,80°)。平滑算法中子阵数目为p=5，每个子阵包括的阵元数l=M-p+1=4。从图2可以看出本文介绍的四元数Toeplitz矩阵重构算法能够对六个完全相干信源解相干得到DOA估计。而对于空间平滑算法找不到同时满足m≥K，p≥K的m和p，所以不能应用空间平滑算法对六个完全相干信源解相干，从图3可以看出空间平滑算法最多只能对4个相干信源解相干。

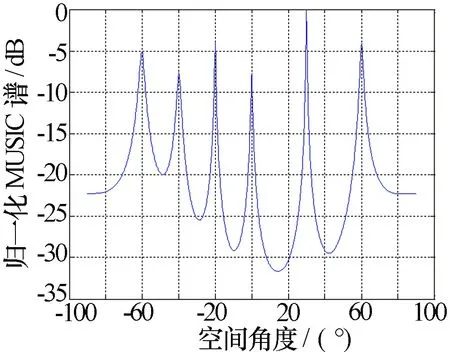
图2 四元数Toeplitz矩阵重构算法对六个相干源的DOA估计

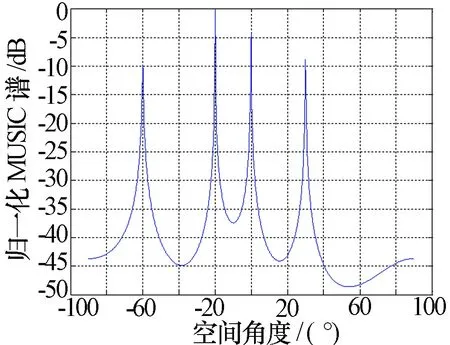
图3 四元数空间平滑算法对四个相干源的DOA估计

3.2 仿真实验2

四元数Toeplitz矩阵重构算法和四元数空间平滑算法分辨性能对比。

对于两个入射角度接近的相干信源，来波方向角分别为40°、35°，极化参数分别为(γ1,η1)=(50°,80°)、(γ2,η2)=(20°,30°)，其余条件与实验1相同。从图4可以看出Toeplitz矩阵重构算法能够在两个相隔较近的来波方向形成了两个尖锐的谱峰，而四元数空间平滑算法只形成了一个谱峰，参数估计失败。图5给出了100次蒙特卡洛实验时波达方向角估计的均方根误差随信噪比变化的曲线。从实验结果可以看出，在入射角度接近时，四元数Toeplitz矩阵重构算法比四元数空间平滑算法具有更低的误差，参数估计性能更优越。

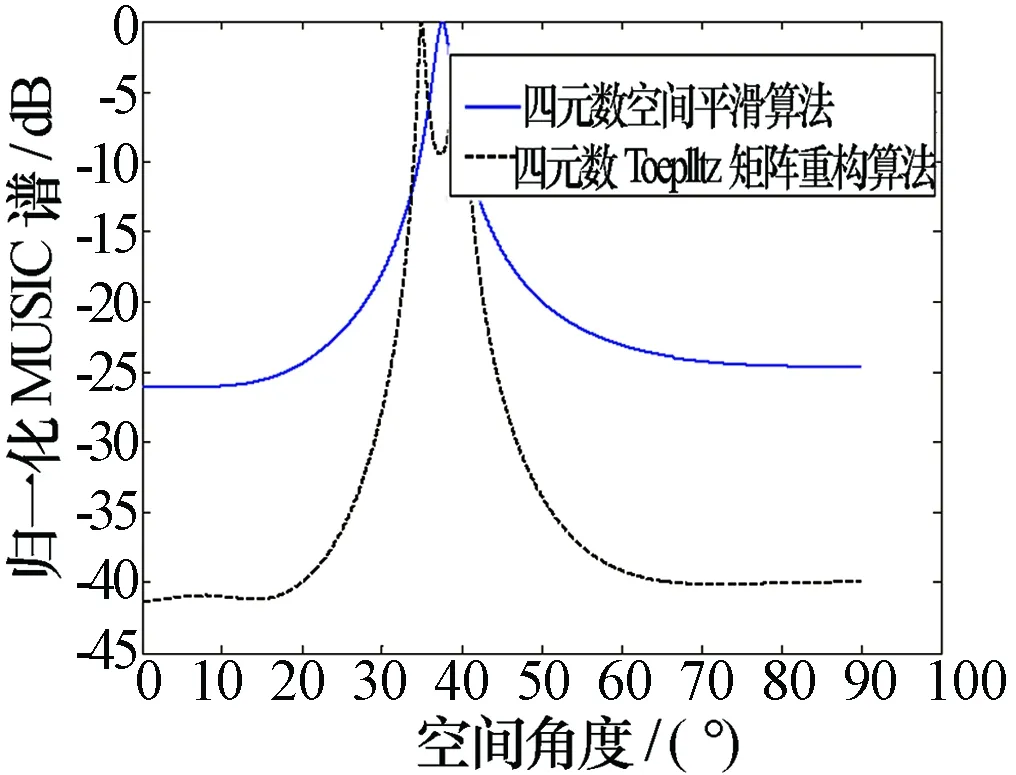
图4 两个入射角度相近的相干源DOA估计

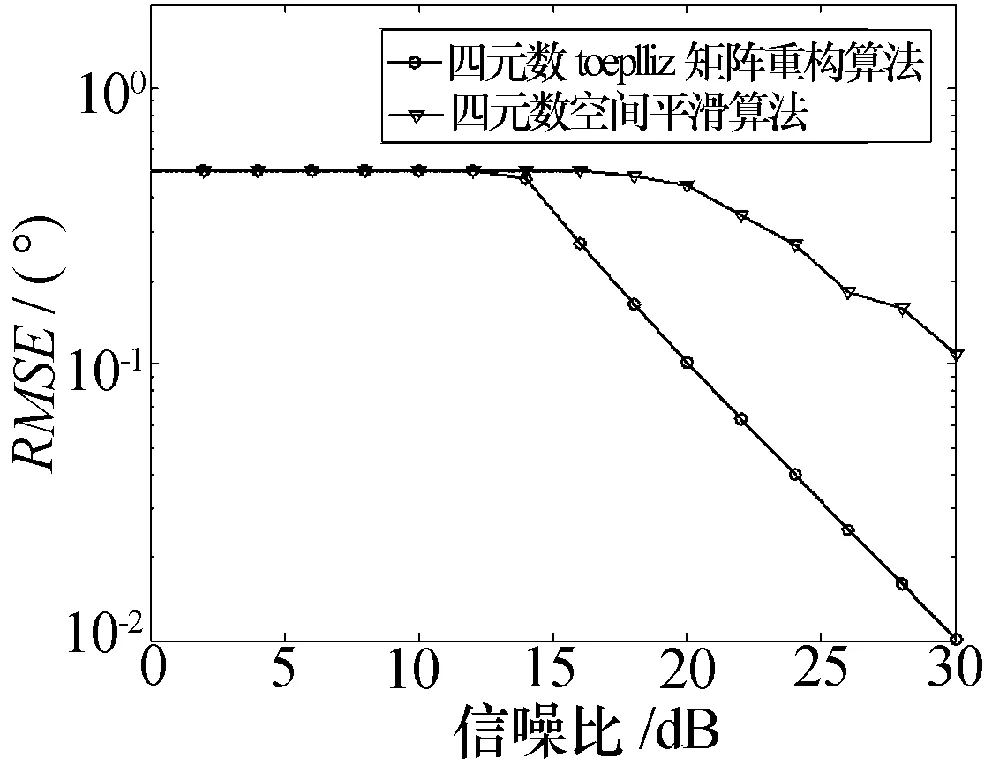
图5 两个入射角度相差较近的相干信源

对于两个入射角度相差较大的相干信源，来波方向角分别为40°、10°，极化参数分别为(γ1,η1)=(50°,60°)、(γ2,η2)=(20°,30°)，其余条件与实验1相同。图6给出了100次蒙特卡洛实验时波达方向角估计的均方根误差随信噪比变化的曲线。从实验结果可以看出，在入射角度相差较大时，四元数Toeplitz矩阵重构算法比四元数空间平滑算法具有更低的误差，参数估计性能更优越。综上可以看出无论两信号入射角度相距如何，四元数Toeplitz矩阵重构算法都比四元数空间平滑算法具有更好的估计性能。

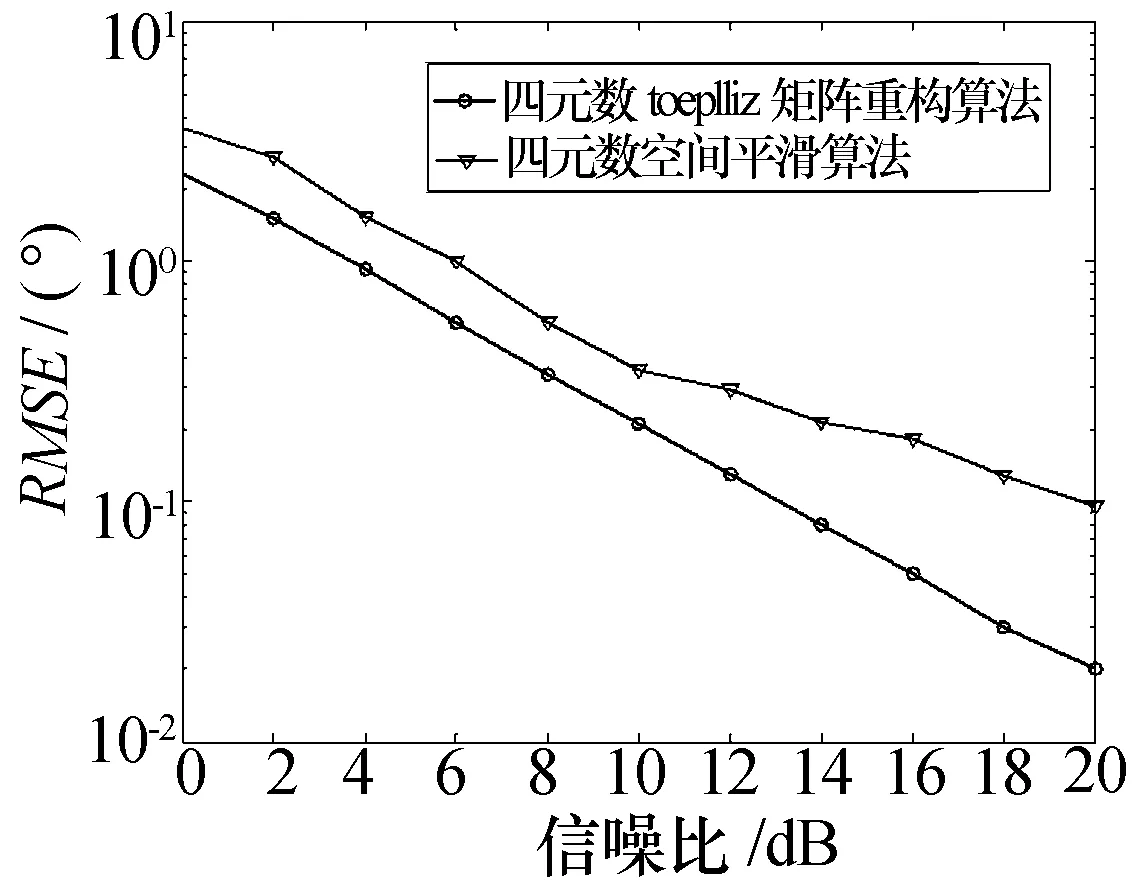
图6 两个入射角度相差较远的相干信源

3.3 仿真实验3

快拍数对四元数Toeplitz矩阵重构算法和四元数空间平滑算法性能的影响。

入射信号信噪比SNR=10 dB，其余条件与实验2相同。图7给出了波达方向角估计的均方根误差随快拍数变化的曲线。从实验结果可以看出，四元数Toeplitz矩阵重构算法的收敛速度很快，随着快拍数增加，两种算法的DOA估计误差越来越小。在相同快拍数的条件下，四元数Toeplitz矩阵重构算法比四元数空间平滑算法具有更好的估计性能。

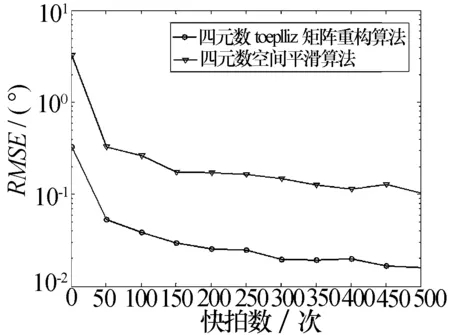
图7 DOA估计均方根误差随快拍数变化曲线

4 结束语

对于电磁矢量阵列的相干信源参数估计问题，本文提出了一种四元数Toeplitz矩阵重构算法，利用四元数的特性，将入射信号的所有信息都用到了算法中。同时利用所有阵元与参考阵元的相关函数进行排序构成了Toeplitz矩阵，实现了解相干，获得了较好的参数估计。与四元数空间平滑算法相比，该算法不需要减少阵列的有效孔径，从而增加了相干信源估计个数。通过仿真实验表明了对于入射信号到达角的估计，四元数Toeplitz矩阵重构算法比四元数空间平滑算法具有更优的性能。

[1] WONG K T, YUAN X. Vector cross-product direction-finding with an electromagnetic vector sensor of six orthogonally oriented but spatially noncollocating dipoles/loops[J]. IEEE Transactions on Signal Processing, 2011, 59(1): 160-171.

[2] KORSO M N, BOYER R. Statistical resolution limit of the uniform linear cocentered orthogonal loop and dipole array[J]. IEEE Transactions on Signal Processing, 2011, 59(1): 425-431.

[3] SCHMIDT R O. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276-280.

[4] ROY R, KAILATH T. ESPRIT estimation of signal parameters via rotational invariance techniques[J]. IEEE Transactions on Acoustic Speech and Signal Processing, 1989, 37(7): 984-995.

[5] 徐友根, 刘志文. 电磁矢量传感器阵列相干信号源波达方向和极化参数的同时估计：空间平滑方法[J]. 通信学报, 2004, 25(5): 28-38. XU Yougen, LIU Zhiwen. Simultaneous estimation of 2-D DOA and polarization of multiple coherent sources using an electromagnetic vector sensor array[J]. Journal of China Institute of Communications, 2004, 25(5): 28-38.

[6] 王布宏, 王永良, 陈 辉. 相干信源波达方向估计的加权空间平滑算法[J]. 通信学报, 2003, 24(4): 31-40. WANG Buhong，WANG Yongliang, CHEN Hui. Weighted spatial smoothing algorithm for direction of arrival estimation of coherent sources[J]. Journal of China Institute of Communications, 2003, 24(4): 31-40.

[7] 余 莉. 利用空间平滑差分算法进行DOA估计[J]. 现代雷达, 2008, 30(8): 87-90. YU Li. Spatial smoothing difference algorithm for DOA estimation of coherent sources[J]. Modern Radar, 2008, 30(8): 87-90.

[8] RAHAMIM D, TABRIKIAN J. Source localization using vector sensor array in a multipath environment[J]. IEEE Transactions on Signal Processing, 2004, 52(11): 3096-3103.

[9] HE J, JIANG S. Polarization difference smoothing for direction finding of coherent signals[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(1): 469-480.

[10] 虞 飞，陶建武, 陈 诚. 鲁棒的四元数空间平滑算法[J]. 信号处理, 2011, 27(9): 1352-1358. YU Fei, TAO Jianwu, CHEN Cheng. A robust quaternion spatial smoothing algorithm[J]. Signal Processing, 2011,27(9): 1352-1358.

[11] 娄 毅. 基于四元数的极化-DOA估计算法研究[D]. 哈尔滨：哈尔滨工业大学，2013. LOU Yi. Research of polarization-DOA estimation algorithm based on quaternion[D].Harbin: Harbin Institute of Technology, 2013.

[12] 蔡云霄. 基于电磁矢量传感器阵列相干源DOA估计的研究[D]. 长春：吉林大学，2010. CAI Yunxiao. Study on the DOA estimation for coherent signals with electromagnetic vector sensor array[D]. Changchun: Jilin University, 2010.

[13] 王永良. 空间谱估计理论与算法[M]. 北京：清华大学出版社，2004. WANG Yongliang. Spatial spectral estimation theory and algorithm[M]. Beijing: Tsinghua University Press, 2004.

张远芳 女，1990年生，硕士研究生。研究方向为阵列信号处理。

李会勇 男，1975年生，教授，博士和硕士生导师。研究方向为自适应及阵列信号处理、雷达系统及信号处理。

谢菊兰 女，1981年生，副教授，硕士生导师。研究方向为自适应及阵列信号处理、雷达系统及信号处理。

Quaternion Toeplitz Matrix Reconstruction Algorithm Based on Electromagnetic Vector Sensor Array

ZHANG Yuanfang，LI Huiyong，XIE Julan

(School of Electronic Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China)

For DOA estimation of coherent sources based on electromagnetic vector sensor array, spatial smoothing algorithm reduced the number of array aperture. A quaternion Toeplitz matrix reconstruction algorithm is proposed. First of all, receiving signal model is established according to the orthogonal property of quaternion, orthogonal structure of two components keeps well for electromagnetic vector sensor array and at the same time DOA and polarization information can be ensured in the reconstruction matrix. Then hermitian Toeplitz matrix is constituted based on the receive data's correlation function between each array element and reference array element. Compared with spatial smoothing algorithm, it increases the number of coherent sources that can be estimated. In the condition of low signal-to-noise ratio and close incident angles, it has better estimation performance. The simulation experiment proves the correctness of the algorithm.

electromagnetic vector sensor array; coherent; quaternion; Toeplitz matrix

10.16592/ j.cnki.1004-7859.2016.04.010

国家自然科学基金资助项目(61371184，61301262)；中国博士后科学基金特别资助项目(115719)；中央高校基本科研业务费资助项目(ZYGX2013J022)

张远芳 Email：yaoyuanstar@hotmail.com

2015-11-23

2016-01-25

TN957；TN911.7

A

1004-7859(2016)04-0042-04