直观性教学法在最优化课程中的应用案例
2016-02-22刘德民侯江霞新疆大学数学与系统科学学院新疆乌鲁木齐830046
刘德民 侯江霞(新疆大学数学与系统科学学院,新疆乌鲁木齐830046)
直观性教学法在最优化课程中的应用案例
刘德民侯江霞
(新疆大学数学与系统科学学院,新疆乌鲁木齐830046)
一、最优化课程的教学特点和直观性教学法的必要性
最优化是应用数学的一个分支,主要研究目标函数在某个集合上取极值的理论和算法,它有着悠久的研究历史。伴随着现代化科学与技术的进步,最优化的理论和算法已经在工程和科学研究的方方面面得到了发展和应用,发挥其越来越大的作用。例如,在航空航天科学科,翼型的最优气动力学设计与飞行器的最佳飞行轨迹;在经济与管理学科,股票或商品的最优定价及物流配送最优路径问题;在石油天然气工业领域,油气输送的最优管道设计及复杂岩性储集层测井的最优评价等。
最优化课程具有如下基本特点:
1.内容跨度大,需要基础知识扎实。最优化理论和算法的来源背景丰富,研究方法多样,因此需要在高等数学、线性代数、大学物理,数学模型以及泛函分析等数学基础课程及程序设计等计算机课程的基础上予以展开,所以开设这门课程之前不仅要求学生具备很好的数学分析和解析求解的能力,还需要具有很好的算法设计和程序研制能力。
2.内容多,学时少。最优化课程主要讲授线性规划的单纯形方法及对偶原理,线性与非线性规划问题的最优性条件,一维搜索,使用导数的最优化方法(如最速下降法,共轭梯度法等)、惩罚函数法、二次规划、组合优化、动态规划、整数规划等内容。通常这门课安排一学期讲完,每周四节,其中三节理论课,一节实验课。加之要提前给学生讲解程序设计的相关内容,因此理论课的时间比较少,而实验课也很难有好的授课效果。
3.数学理论丰富,算法众多。由于最优化课程内容庞杂,而每部分都有各自的数学理论知识和算法,因此最优化课程涉及到的理论非常丰富,算法非常众多。从离散数学到连续数学、从静态标规划到动态规划、从线性规划到非线性规划、从单目标规划到多目标规划等等。
4.直观性需求高。最优化课程中有很多概念和定理都很理论化,缺乏直观性,学生在学习时往往是被动的接收,机械的记忆,并不能很好的理解。由于最优化课程自身的特点,需要结合现代化的教学和多媒体手段,丰富与充实教学内容,加强教学内容直观性的研究和实现。如果能采用更为直观的方式将这些内容展现给学生,将会提高学生的学习效率,改善教学效果。基于最优化课程的如上特点,直观性教学法在最优化课程中的应用非常有必要。直观性教学法是指在直观性的教学原则和教学手段下的课程讲授。直观性教学法在最优化课程中的应用,是指结合最优化课程的自身特点,在直观性的教学原则下,采用不同的直观性教学手段,提高学生对抽象理论与具体问题之间的认识,增进学生对数值分析课程基本理论的理解,提升学生的学习效率,改善教学效果。
二、最优化课程中直观性教学法案例
在最优化课程的讲授过程中可以采用多种直观性的教学手段来改善和提高教学效果。例如在讲解线性规划时,可以采用通常的表格形式[1];讲解具体算法时可以采用流程图和程序代码演示等直观形式[2]等。作为案例这里再考虑几类直观性方法。
(一)语言直观
语言直观主要是指教师在教学过程中对抽象的数学概念或定理用形象的语言进行阐释,使学生获得直观感受的一种直观教学方法。
例如在讲解到线性规划的对偶定理时讲到:“若原问题和对偶问题中有一个问题存在最优解,则另一问题也存在最优解,且两个问题的目标函数值相等”。对该定理的证明可以采用多种方法,如凸集分离定理等[1],往往比较抽象。为此我们以买家和卖家分别为研究对象可以得到一对对偶问题,买家想要花费最少的钱获得商品,而卖家想要赚取最大利润。显然如果买卖能够达成,也即存在最优解,则买家花费的钱和卖家获得利润是相等的,也即原问题和对偶问题的目标函数值相等。通过这样一个实例,相信学生会对该定理记忆深刻。
(二)图形直观
图形的优点是它所反映的信息简洁、直观、丰富,便于理解问题。例如在讲到针对单峰函数的一维无约束极值问题的黄金分割法时,当确定了第k次迭代区间为[ak,bk],k=0,1,…后,需要插入两个试探点姿资,滋k缀[akbk],姿资约滋k通过判定姿k,滋k,处的函数取值,按照规则若f(姿k)跃f(滋k),则ak+1=姿资,bk+1=bk;否则ak+1=ak,bk+1=滋k,可以确定下一次迭代区间[ak+1,bk+1],这里要求如下两个条件成立:

其中参数0约a约1为待定参数。通过求解(1),(2)两式,可以得到

事实上,要通过(1),(2)两式得到姿资,滋k的表达式(3)和(4)是比较麻烦的。根据黄金分割法的算法过程,可以做出黄金分割法示意图,由该图知道(3)和(4)两式显然成立。
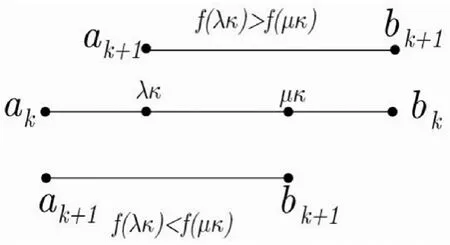
黄金分割法示意图
(三)公式直观
公式直观是指教师借助公式的具体形式,简洁而直观的表现教学内容,增强学生对知识点的把握和理解。例如在讲解共轭梯度法时,首先是针对二次凸函数的FR共轭梯度法,这里求解的问题为:
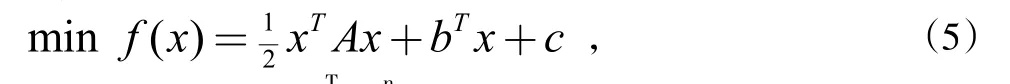
其中x=(x1,x2…,xn)缀R,A是对称正定矩阵。这里对矩阵A对称正定的要求从何而来?我们可以给出如下直观性的解释。
首先考虑对矩阵A的对称性要求,即A=AT。通过对目标函数f(x)求梯度,可以得到
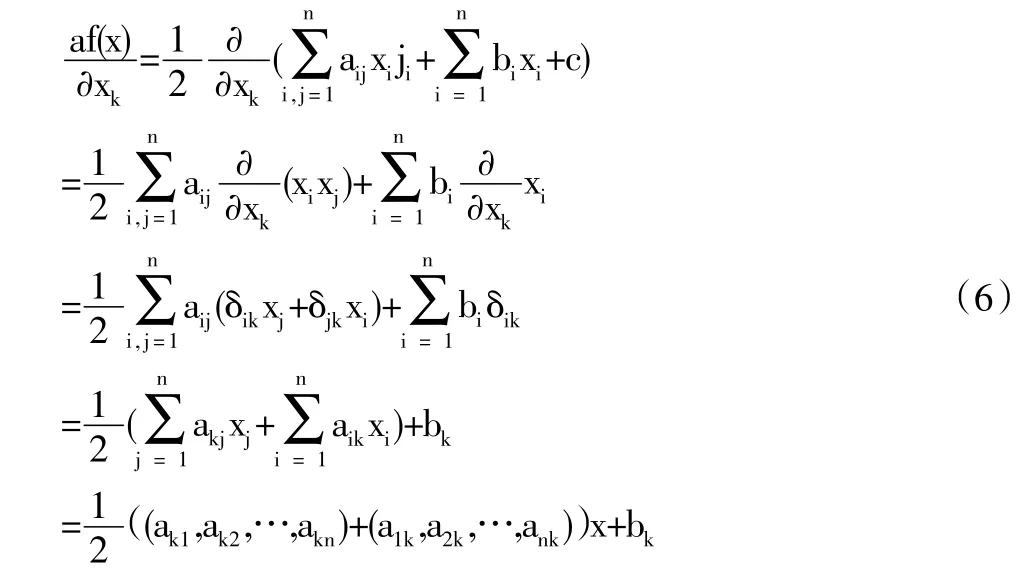
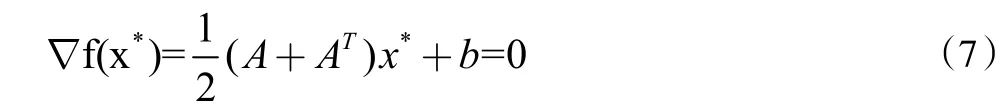
由此按照极值的必要条件可得,若x*为目标函数f(x)的极小点,则满足成立。因此若矩阵A满足对称性要求,则根据(7)式知此时x*满足线性代数方程组Ax*+b=0。
关于对矩阵A的正定性要求可以如下解释:一方面从理论上来看这是函数f(x)极值存在的充分性条件要求之一,另一方面结合对矩阵A的对称性要求可知,此时矩阵A的特征值全为正,且存在正交阵P=(P1,P2,…,Pn),使得P-1AP=PTAP=撰成立,其中矩阵A是由矩阵A的特征值姿1,姿2,…,姿n所构成的对角阵,PiTPj=啄ij,i= 1,2,…,n。由于A=P撰PT成立,如果做正交线性变换y=PTx,即x=Py,也即将x看做由pi,i=1,2,…,n,为标架所生成的直角坐标系下的点,并令=bTP,则易得
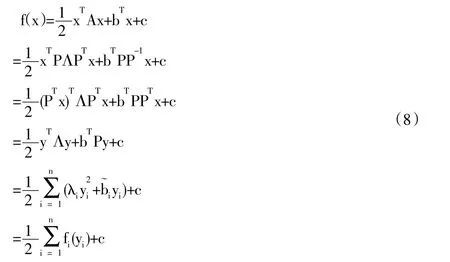
注意到确定一个矩阵的特征向量同样是非常困难的,因此上面的理论并不适合于数值计算。为了克服这个困难,引入一组关于对称正定矩阵A共轭的向量组qi,i=1,2,…,n,它们是线性无关的,且满足当i屹j,i,j=1,2,…,n时成立qiTAqj=0,同时当i=1,2,…,n时成立qiTAqj跃0。进一步令匝=(q1,q2,…,qn),并作仿射变换x=匝z,该变换的几何意义是将x看做由qi,i=1,2,…,n所生成的仿射标架下的点,通过简单地计算可得,
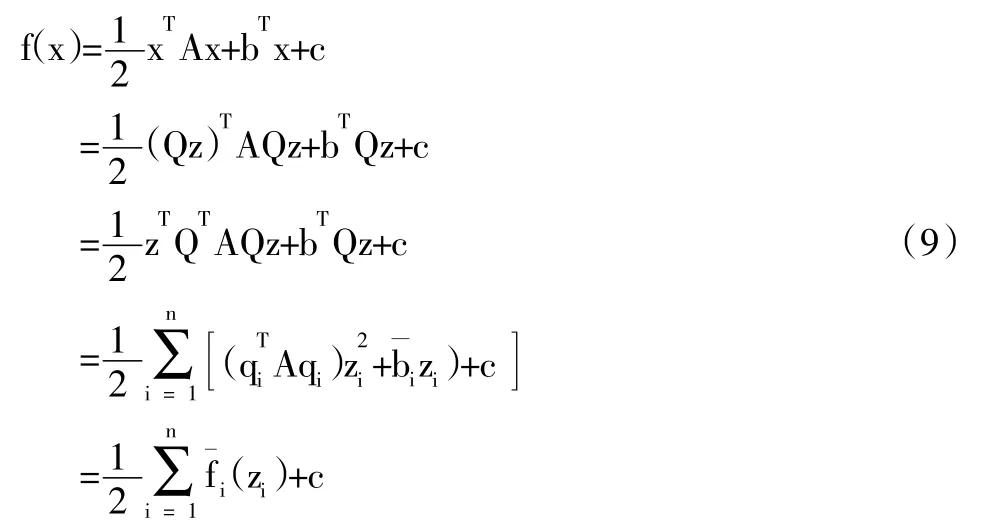
同样是将原目标函数f (x)的极小值问题转化为n个独立的或分离变量的目标函数fi(zi)的极小值问题。注意到此时共轭向量组qi,i=1,2,…,n的选取容易的多,从而非常便于数值计算。比较公式(8),(9)可知,通过直角坐标变换或者仿射坐标变换均可使得原始的目标函数变换为变量分离形式,且不论哪种变换,都至多需要n步即可求得极值,该结论正是课本中这部分内容的主要定理和结论[1],通常采用数学归纳法证明,缺乏直观性理解。
三、结束语
本文结合作者在最优化课程教学中的实践经验,讨论了直观性教学法在最优化课程中应用的必要性,并给出了直观性教学法的具体案例。教学实践表明直观性教学法可以提升学生学习最优化课程的兴趣、增进学生对最优化课程中抽象理论的理解,从而提高学生学习的效果。
参考文献
[1]陈宝林.最优化理论与算法[M].北京:清华大学出版社,2009. [2]施光燕.最优化方法[M].北京:高等教育出版社,2009.
摘要:通过归纳最优化课程的基本特点,分析了直观性教学法在最优化课程中应用的必要性。借助具体的教学案例,演示了语言直观、图形直观与公式直观在最优化课程讲授时的具体实施。教学实践表明适当的直观性教学可以促进学生对抽象理论的理解,从而改善教学效果。
关键词:最优化;直观性教学法;教学案例
侯江霞,单位:新疆大学数学与系统科学学院。
Abstract:By generalizing the features of optimization course, this paper analyzes the necessity of the application of the intuitive teaching method in optimization course. Through the specific teaching cases, the paper demonstrates the implementation of intuitionist teaching aids, such as the language intuition, intuition of graph, and formula intu-ition. Teaching practices have shown that the intuitive teaching method can effectively promote students' understand-ing of the abstract theory and enhance the teaching effects.
Keywords:optimization; intuitionist teaching method; teaching case
作者简介:刘德民,单位:新疆大学数学与系统科学学院。
中图分类号:G642
文献标志码:A
文章编号:2096-000X(2016)02-0085-02
