“数与形”例2的解读与思考
2016-02-16徐英飞李新根
□ 徐英飞 李新根
“数与形”例2的解读与思考
□ 徐英飞 李新根
对于人教版六年级上册数学广角“数与形”例2,教材编者认为学生能发现加数的规律,也能发现“和的分子总是比分母小1”的结论,并推理出“随着加数越来越多,和越来越接近于1”,而且通过画图,也能得出总和等于1。但事实上,学生很少认可总和等于1,究其原因是因为他们把无限加数当作有限个数来思考了,画图也一样,而这一点,正是教学的真正突破口。
数与形 有限 无限 极限
“数与形”是人教版六年级上册数学广角中(第107页)的内容。由于是新增内容,所以一线教师对它的研究比较少,其中例2是这样的:计算。

一、教材解读
(一)教材的编写意图
根据书本第107页上的编写意图,是要让学生通过观察与计算,发现加数的规律与和的规律(即后一个加数是前一个加数的,和的分子总是比分母小1,随着加数越来越多,和就越来越接近于1),从而感受到什么叫“无限接近”。对于结果,教材编者认为无法一一穷举,但可以通过观察到的规律进行“无穷无尽”的类推,让学生在这一过程中体会推理和极限思想。
教材第108页上的小精灵说:“可以画个图来帮助思考,用一个圆或一条线段表示‘1’。”另一位男生说:“从图上可以看出这些分数不断加下去,总和就是1。”从这页的编写意图看,就是要通过数形结合的方式,让学生知道最终的结果是1。即在圆形上分别有规律地表示出这些加数,当这个过程无止境地持续下去时,所有的扇形就会把整个圆占满(线段也是同样道理),这时,这些数相加之和就为1了。
(二)《教师教学用书》中的说明
教师教学用书中说道:可利用分数意义的直观模型,使学生直观地理解“无限”的抽象概念;让学生通过计算,发现和越来越趋向于1,感受什么叫“无限接近”;利用观察到的规律进行“无穷无尽”的类推,使学生在这一过程中体会推理和极限思想;“无限”的概念非常抽象,学生不易理解,例如,学生会说最终的结果接近于1,但永远不可能为1。事实上,对于任一有限和,都可以通过再加一项来得到更小的和,这就是“极限”的核心思想。这里有几个关键词:无限、无限接近、极限。
二、教学困惑
对于例2,笔者曾进行过教学尝试,先出示例2让学生进行观察,然后再计算,一切正如书本第107页所料,学生不仅观察出了加数的规律,还发现“和的分子总是比分母小1”,并推理出“随着加数越来越多,和越来越接近于1”,这着实让他们体验了一回什么是“无限接近”。
但当问起“和可不可能等于1”时,没有一个人认可,因为他们觉得无论怎么加下去,和的分子总是比分母小1。于是让学生根据分数的意义画一画图,教师再配以课件演示,结果还是不行。因为他们始终认为不论怎么画,整个图形还是缺一块,所以永远到不了1。至此,教学陷入了僵局,所有的推理、画图都显得苍白无力。
三、重新认识
为了解决教学中的困惑,笔者查阅了相关资料,特别是在王永春老师所著的《小学数学与数学思想方法》一书中找到了答案。
(一)对极限思想的认识
书中关于“极限思想”,有这样几段文字:①极限思想是用无限逼近的方式来研究数量变化趋势的思想,这里要抓住两个关键语句:一个是变化的量是无穷多个,另一个是无限变化的量趋向于一个确定的常数,两者缺一不可。如自然数列是无限的,但是它趋向于无穷大,不趋向于一个确定的常数,因而自然数列没有极限。②当我们面对无限的问题时,就不要再用有限的观点来思考,要进入无限的状态。比如0.999…=1,有的教师认为:无限循环小数的位数是无限的,和永远达不到1,永远小于1。这是一种片面的观念,是因为用有限的观点来看待无限造成的,这样的问题在数学上应该用极限的方法来解决。③极限方法只关注一个无限的变化过程的确定趋势是什么,只要趋势确定并且符合极限的定义,那么这个无限变化的过程的结果就用极限来表示,它就是一个解决问题的方法而已,只要符合极限的规则和逻辑,就可以用极限来表示无限变化的过程的结果,它并不关心这个无限变化的过程何时能到达极限,它在本质上不同于有限个数的和。
也就是说,如果某个变化的量“无限逼近”于一个确定的数值,那么这个定值就叫作变量的极限。教材编写意图就是为了让学生获得这样的感悟:随着加数越来越多,和就越来越接近于确定数1,当加数个数无限多时,和就是1。
(二)对学生困惑的认识
其实想了1万个就才1万个,想了1亿个就才1亿个。但例题中的加数个数是无限的,无论到什么时候都不能断开,所以“整个数列的和”必然是另外一种状况。
画图也一样,是不能停的,一旦停了,就会有空缺,而现在是无限地画下去,所以肯定看不到空缺。
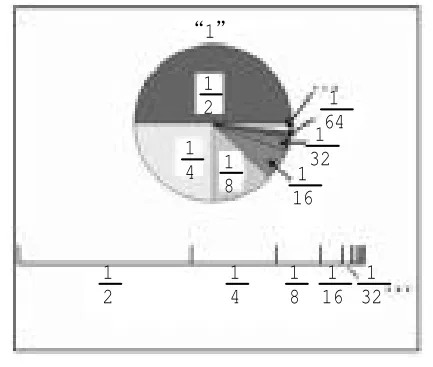
四、新的思考
分析了学生的困惑之后,笔者对这个内容的教学有了新认识。前面的环节,可以像教材编写的那样,让学生经历一个观察、计算、画图的过程。接下来,必须让学生清楚“无限个加数相加,和可能是无穷大,也可能是逼近于某个确定的常数”。比如1+2+3+4+…的和就是无穷大,而的和就是逼近于1。接下来让学生思考:当这个和无限地逼近这个常数时,会不会就等于这个常数呢?此时可借助于“刘徽的割圆术”和“求圆面积的方法”,书本第68页上有这样的描述:“刘徽从圆内接六边形开始,将边数逐次加倍,得到的圆内接正多边形就逐步逼近圆,割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣。”这是什么意思呢?就是说当正六边形的边数无限倍增的时候,它就会无限地逼近圆,最后就变成了圆。另外,从圆面积的探究过程中也可以发现,当把圆等分成若干个小扇形,然后拼成一个近似的长方形,当分的份数越多,拼出的图形就越接近长方形,最后就变成了长方形。这些知识的回顾都有利于学生对极限的认识,从而认可例2的结果等于1。
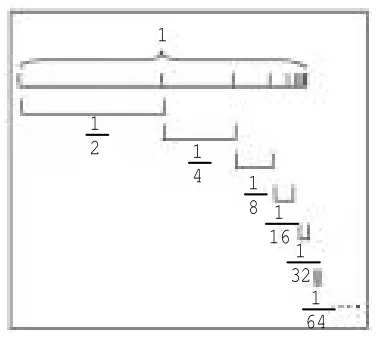
再接着,通过动画演示来让学生明白例2等于1的原因,(如下页图)把整条线段看作“1”,然后用,…分割下去,这样就有无数条小线段。然后再反过来,把这无数条小线段重新拼接起来,结果就是原来的“1”。
最后再来讨论“先前认为和不可能等于1的原因”,那是因为我们都把它当作有限个数来思考了。比如,画图时,总觉得画不满,那是因为我们不画下去了,如果画个不停,就看不到空缺。
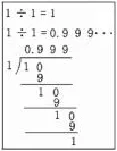
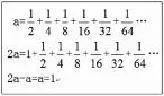
如果还有时间,可再作些补充,比如0.999…的小数点后面有无限多个9,那么它等不等于1呢?因为 0.333…×3=0.999…,,所以0.999…=1;还可以假设1除以1不够除,那么只能商0,于是就有了右边的算式。
总之,这个内容的教学,既要顺着学生的思维,又要让他们有新的突破。通过经验回顾(割圆术、求圆面积方法)和数形结合,可以让学生明白例2等于1的原因,还可以感悟极限思想,有了这种思想,不仅可以降低解决问题的难度、优化解题过程,还能对初、高中的数学学习有帮助。所以学好这节课,意义深远。
[1]王永春.小学数学与数学思想方法[M].上海:华东师范大学出版社,2014(7).
(浙江省桐乡市崇德小学 314511浙江省桐乡市教育局教研室 314500)
