变浅效应调制的复杂动态海面杂波特性研究
2016-02-15袁晴晴
聂 丁,袁晴晴,张 民
(1.西安电子科技大学 物理与光电工程学院,陕西 西安 710071; 2.上海机电工程研究所,上海 201109)
变浅效应调制的复杂动态海面杂波特性研究
聂 丁1,袁晴晴2,张 民1
(1.西安电子科技大学 物理与光电工程学院,陕西 西安 710071; 2.上海机电工程研究所,上海 201109)
为了解近岸浅水域雷达海杂波特性,针对变浅效应调制的近岸海面,分别用非线性水动力模型对海面进行几何建模,用二阶小斜率近似模型对海面杂波进行建模。通过对海面散射场的散射振幅对粗糙海面的斜率作幂级数展开,获得相应的散射场,讨论了近岸动态海面后向散射特性和散射回波的多普勒谱特性。研究发现:在小风区不同水深的海面斜率差异较小,在大风区不同水深的海面斜率差异变大,表明水深对波浪形状的影响随风区增大而变大;在相同条件下,浅水与深水区域对应的海面后向散射系数差值在风区较大时更明显,大风区的浅水海面多普勒谱中心频率增幅也最为明显,尤其是对水平极化。研究对近岸海域雷达目标探测和识别、滨海区域海洋遥感及相关应用有一定的指导意义。
后向散射; 海杂波; 小斜率近似; 近岸海面; 变浅效应; 非线性水动力效应; 雷达散射截面; 多普勒谱
0 引言
海面后向电磁散射回波即为海杂波,相关特性的研究在海洋监测、目标识别和海洋环境遥感等领域有广泛的应用,近年来获得了大量关注。雷达后向散射系数和雷达散射回波多普勒谱是研究动态海面回波最主要的两个指标,在相关领域的研究中被广泛采用[1-2]。目前,大多数研究主要针对深海海洋环境中的雷达海杂波特性,而对与人类活动关系更紧密的近岸区域未被给予足够的重视。相对于深海环境,近岸区域水深较浅,波浪形态及斜率等会受水深的影响而变得更复杂,另外还有波浪卷曲、破碎、白沫等复杂结构产生,使相应的电磁散射机理研究更困难。近岸这种复杂的环境对海滨目标监测和识别领域提出了更大的挑战,因此对近岸海域海杂波特性研究亟待开展。文献[3]基于实验测量数据提出了一种能对有限水深区域的风浪进行合理描述的海谱模型,简单易用,却未对相关的近岸海面电磁散射特性进行深入研究。文献[4]对滨海环境中的X波段雷达海杂波特性进行了详细描述,但未探讨相应的回波多普勒谱特性。本文对二维近岸海面雷达杂波的后向散射系数和多普勒谱同时展开研究,而并非仅限于传统的深海海域。在研究海面电磁散射过程中,多种数值方法和近似方法都发挥了重要作用,如多阶矩感应方法(MOMI),双尺度方法(TSM),小斜率近似方法等,均有各自的优点[5]。小斜率近似方法的二阶解(SSA-Ⅱ)有较高的计算精度,也得到了许多数值方法的验证,在入射角较大时表现良好,而且与矩量法和积分方程等方法相比,其计算公式简单、计算效率高。因此,本文先基于非线性水动力模型对近岸海面进行几何建模,再根据海面几何模型,结合SSA-Ⅱ模型对变浅效应调制的近岸动态海面后向散射特性和散射回波的多普勒谱特性进行仿真计算,并分析了计算结果,为海洋背景中目标监测提供理论依据。
1 变浅效应调制的近岸海面几何建模
对海面的动态结构进行尽可能精确的描述是研究动态海面杂波特性的先决条件,因此,传统的基于高斯谱的海面几何建模需作进一步改进,对不同尺度波浪间的非线性水动力作用应予以足够的重视,以描述趋近于真实环境中海浪的细微结构信息,这对近岸海浪的建模尤为重要。一般在海浪从深海向近岸传播过程中,随着水深不断减小,虽然波浪的传播频率依然不变,但波浪的传播速度不断下降,在该过程中,波与波间的非线性水动力效应变得越发强烈,进一步对波浪的形状产生影响而使之变化,在物理海洋学研究中,该现象被称为变浅效应。基于以上分析,非线性尖浪模型(CWM)较适合对近岸变浅效应调制的海浪进行几何建模。
本文用谱合成技术对动态海面进行建模,其基本要点是:将海面视作不同次谐波的叠加,这些谐波的幅值是与海谱成特定比例的独立的高斯随机变量,因此对这些随机变量进行快速傅里叶变换(FFT),在频域用海谱这一特定的滤波器对其进行滤波,再作快速傅里叶逆变换(IFFT)就能得到海面的空间高度起伏。海谱作为整个变换过程中的核心,其准确性对建模结果有较大的影响。本文采用适于描述近岸浅海域风浪的海谱进行建模,该海谱基于海岸工程的相关观测和研究结果得出,是海水深度和风区的函数,有

(1)
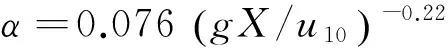
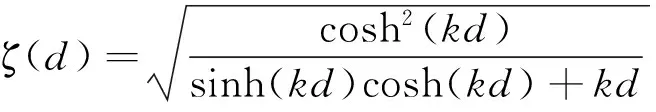
(2)
此处:X为风区;u10为海平面上方高度10 m处的风速;g为重力加速度;k为海浪波数;d为海水深度[6]。则,空间坐标r处时刻t海面高度起伏h可表示为
h(r,t)=∫F(r,k;t)exp(jk·r)dk;
(3)
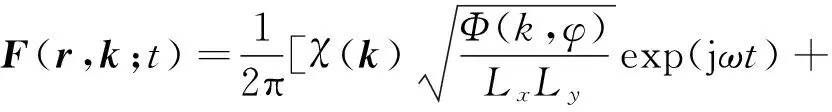
(4)
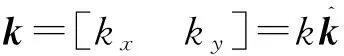
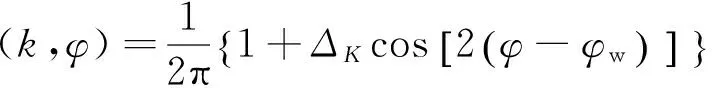
(5)


(6)
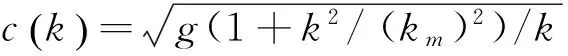
uz=(uf/0.4)×

(7)
kp为谱取峰值时所对应的波数,且kp=gΩ2/(u10)2[7]。
基于式(3)得到的为传统的线性海面,并未加入波浪非线性效应的影响。CWM模型针对这一需求,在海面水平坐标处加入了基于水动力学原理的水平扰动项,使模拟得到的海面具备一定程度的非线性特征,则
Ch(r,t)=
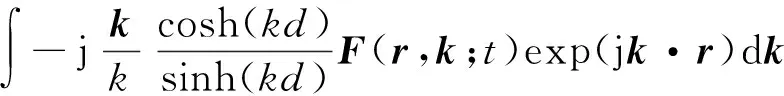
(8)
最终,基于CWM模型的二维变浅效应调制的动态海面上时刻t任一点的坐标可表示为(r+Ch(r,t),h(r,t))[8]。
在模拟风速10 m/s条件下,设d分别为5,100 m,X分别为10,100 km,二维变浅效应调制的动态海面沿x轴向抽取得到的一维剖面的表面斜率如图1所示。由图1可知:在小风区(X=10 km)中,两种不同水深对应的海面斜率差异较小,几乎可忽略;在大风区(X=100 km)中,上述差异明显增大,浅水对应的海面斜率显著大于深水。这一定程度反映出水深因素对波浪形状的影响随风区增大而逐渐明显,与实验观测结果一致[9]。

图1 二维变浅效应调制的海面沿x轴向抽取得到的一维剖面的表面斜率Fig.1 Slopes of 1-D profiles of simulated 2-D sea surfacesmodulated by shoaling effect in x-axis direction
2 基于SSA-Ⅱ模型的变浅效应调制海面杂波建模
因SSA-Ⅱ模型能较好地兼顾计算效率和计算精度,在海面电磁散射相关领域内应用广泛。因此,本文采用SSA-Ⅱ模型对变浅效应调制海面杂波进行建模。考虑单位平面电磁波入射到面积为Lx×Ly的二维海面,入射场可表示为
Ei=G(r,h)exp(-jki·r+jqih).
(9)
式中:G(r,h)为锥形波函数,用于控制入射波束的形状和强度,消除边缘效应;Ki为入射波矢量,且Ki=[ki-qi];Ks为反射波矢量,且Ks=[ksqs][10]。此处:ki,ks分别为相应的水平分量,且
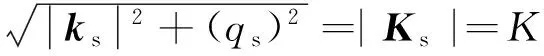
(10)
φi),
(11)
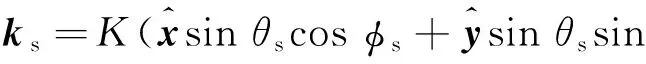
(12)
qi=Kcosθi,
(13)
qs=Kcosθs.
(14)


图2 二维海面电磁散射示意Fig.2 Geometry of 2-D sea-surface scattering problem
则基于SSA-Ⅱ模型的变浅效应调制海面散射振幅可表示为
exp(jξ·t)dξ.
(15)
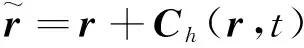
(16)
M为散射矩阵幂级数展开的二阶系数组成的多项式,且
M(ki,ks;ξ)=BII(ki,ks;ks-ξ)+
BII(ki,ks;ki+ξ)+2(qi+qs)B(ki,ks).
(17)
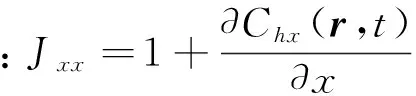
最终,雷达散射系数,即归一化的海杂波幅值可表示为
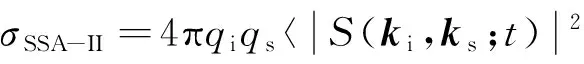
(18)
式中:〈 〉表示多个海面样本求算数平均的结果。
基于由式(15)得到的散射振幅,还可算得散射回波的多普勒谱
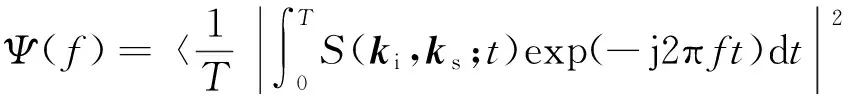
(19)
式中:T为模拟的动态海面的持续时长。
3 计算与讨论
本文用SSA-Ⅱ理论对二维变浅效应调制的海面后向散射系数进行计算。仿真中,雷达电磁波入射频率1.304 GHz,风速10 m/s,海面尺寸117.76 m117.76 m,锥形波波束宽度因子19.63 m,模拟了水平极化(HH-pol)和垂直极化(VV-pol)两种情况。风区分别为10,100,120 km时,不同入射角下浅水(d=5 m)和深海(d=100 m)的海面后向散射系数计算结果差值分别如图3~5所示。图中计算结果为200个海面样本平均后的结果。
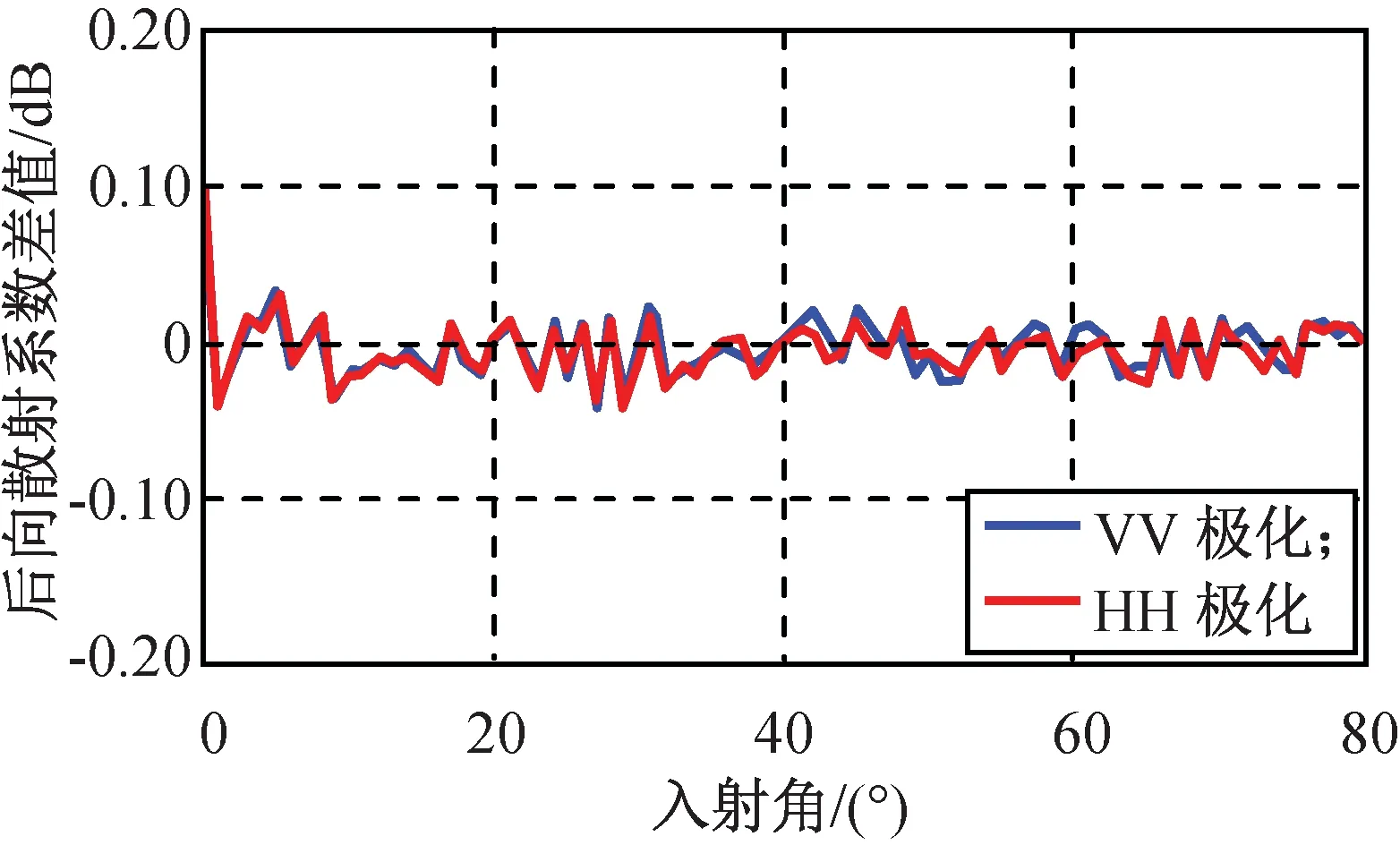
图3 风区10 km下不同水深海面后向散射系数差值随入射角的变化Fig.3 Magnitude differences of NRCS with various depthsand different incident angle for wind fetches 10 km
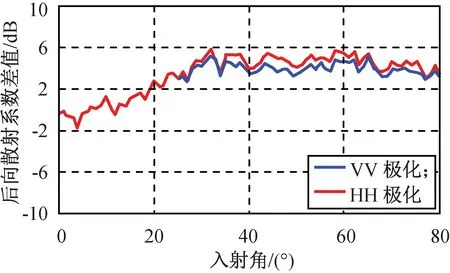
图4 风区100 km下不同水深海面后向散射系数差值随入射角的变化Fig.4 Magnitude differences of NRCS with various depths and different incident angle for wind fetches 100 km

图5 风区120 km下不同水深海面后向散射系数差值随入射角的变化Fig.5 Magnitude differences of NRCS with various depths and different incident angle for wind fetches 120 km
由图3~5可知:随着风区增大,浅水与深海的后向散射系数的差异越来越明显,尤其在中到大入射角下,水平极化和垂直极化皆如此。该现象反映在大风区浅水海域,波浪间的非线性效应变得更强烈,波浪斜率较大的成分有所增加,增强了中到大入射角时在后向散射中占主导地位的波浪类型的比重,进而综合影响了散射系数。此外,与垂直极化相比,水平极化下的结果差值较大,在大风区更是如此,一定程度反映水平极化方式对波浪间的非线性效应更敏感。
对动态海面回波多普勒谱进行了仿真分析。在相同参数条件下,仿真计算了入射角15°,45°,风区10,100 km时不同水深海面散射回波的归一化多普勒谱,结果分别如图6~9所示。

图6 风区10 km、入射角15°不同水深海面散射回波归一化多普勒谱Fig.6 Normalized Doppler spectra of backscattered echoes from sea surfaces for different depths with wind fetches 10 km and incident angle 15°

图8 风区10 km、入射角45°不同水深海面散射回波归一化多普勒谱Fig.8 Normalized Doppler spectra of backscattered echoes from sea surfaces for different depths with wind fetches 10 km and incident angle 45°
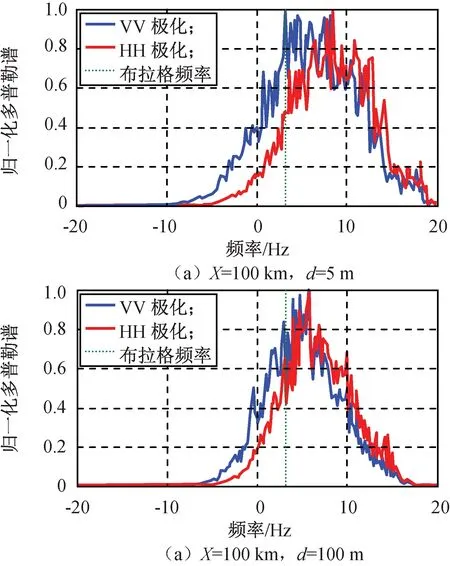
图9 风区100 km、入射角45°不同水深海面散射回波归一化多普勒谱Fig.9 Normalized Doppler spectra of backscattered echoes from sea surfaces for different depths with wind fetches 100 km and incident angle 45°
由图6~9可知:当入射角较小(15°)时,水平极化和垂直极化结果的差异很小,且在各种风区和水深下曲线基本重合,在大风区和小水深时,多普勒谱峰频率明显大于其它情况下的结果;当入射角增大到45°时,各种风区和水深的水平与垂直极化结果都表现出明显差异;类似地,大风区和小水深时,多普勒谱峰频率明显大于其它情况下的结果,水平极化时尤其突出。该现象揭示出:处于较大风区条件下的近岸浅水波浪会受到较强的非线性水动力效应的影响,而且该影响在水平极化方式下尤为显著。
4 结束语
本文根据近岸浅水域海面电磁散射研究的需要,基于水动力学建模方法和电磁建模理论对变浅效应调制的复杂动态海面杂波特性进行了研究。基于二阶小斜率近似方法计算并分析了不同风区和水深时的海面后向散射系数与回波多普勒谱,并基于物理机理对仿真结果进行了分析。本文的研究区别于传统的深海环境海杂波研究,从浅水域波浪形态变化出发,针对近岸浅水区域海浪波的特点进行相对精确的几何建模和后续的电磁散射仿真分析,为近岸海杂波特性分析提供了参考。研究对近岸海域雷达目标探测和识别、滨海区域海洋遥感及相关应用有一定的指导意义。后续研究将包括近岸浅水域海浪和典型目标复合电磁散射特性仿真和分析。
[1] TOPORKOV J V, BROWN G S. Numerical study of
the extended Kirchhoff approach and the lowest order small slope approximation for scattering from ocean-like surfaces: Doppler analysis[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 50: 417-425.
[2] HASSELMANN K, RANEY R K, PLANT W J, et al. Theory of synthetic aperture radar ocean imaging: a MARSEN view[J]. Journal of Geophysical Research Atmospheres, 1985, 90: 4659-4686.
[3] BOUWS E, GÜNTHER H, ROSENTHAL W, et al. Similarity of the wind wave spectrum in finite depth water 1: spectral form[J]. Journal of Geophysical Research, 1985, 90: 975-986.
[4] WARD K D, TOUGH R. Modelling radar sea clutter in littoral environments[C]// 2008 International Conference on Radar IEEE. Adelaide: IEEE, 2008: 82-87.
[5] ELFOUHAILY T M, GUÉRIN C A. A critical survey of approximate scattering wave theories from random rough surfaces[J]. Waves in Random Media, 2004, 14: 1-40.
[6] MCCORMICK M E. Ocean engineering wave mechanics[M]. New York: John Wiley & Sons Inc, 1973.
[7] ELFOUHAILY T M, CHAPRON B, KATSAROS K, et al. A unified directional spectrum for long and short wind-driven waves[J]. Journal of Geophysical Research, 1997, 102: 15781-15796.
[8] NIE D, ZHANG M, WANG C, et al. Study of microwave backscattering from two-dimensional nonlinear surfaces of finite-depth seas[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50: 4349-4357.
[9] YOUNG I R, VERHAGEN L A. The growth of fetch limited waves in water of finite depth: part 1 total energy and peak frequency[J]. Coastal Engineering, 1996, 29: 47-78.
[10] TSANG L, KONG J A, DING K H. Scattering of electromagnetic waves[M]. New York: John Wiley & Sons Inc, 2001.
[11] VORONOVICH A G, ZAVOROTNY V U. Theoretical model for scattering of radar signals in Ku- and C-bands from a rough sea surface with breaking waves[J]. Waves in Random Media, 2001, 11: 247-269.
Study of Complex Dynamic Sea Clutter from Sea Surfaces Modulated by Shoaling Effect
NIE Ding1, YUAN Qing-qing2, ZHANG Min1
(1. School of Physics and Optoelectronic Engineering, Xidian University, Xi’an 710071, Shaanxi, China;2. Shanghai Electromechanical Engineering Institute, Shanghai 201109, China)
To understand the characteristics of radar sea clutter in nearshore area, geometric model was established by nonlinear hydrodynamic model for sea surface and electromagnetic model was developed by second-order small slope approximation method for sea clutter which was applied to the sea surfaces modulated by shoaling effect. The scattering electromagnetic field could be obtained with a regular expansion of scattering amplitude in terms of roughness slope. The dynamic sea clutter backscattering characteristics and Doppler spectrum features were analyzed. It found that the slope differences among various sea depths in small wind fetch were not obvious but the slope differences became larger in big wind fetch, which meant that effect of sea depth on wave would be obvious with wind fetches becoming large. With a larger fetch, the excess of backscattering coefficient for small depth sea over that for deeper sea increased, and Doppler shift also had an obvious growth, especially for horizontal polarization. This study has certain guiding significance for target detection and recognition, and remote sensing in coastal area.
Backscattering; Sea clutter; Small slope approximation; Nearshore sea surface; Shoaling effect; Nonlinear hydrodynamic effect; Radar cross section; Doppler spectrum
1006-1630(2016)06-0020-06
2016-08-01;
2016-09-12
国家自然科学基金资助(41306188)
聂 丁(1985—),男,副教授,主要从事地海背景雷达通信环境电磁散射及环境遥感建模分析。
TN011
A
10.19328/j.cnki.1006-1630.2016.06.002
