基于点云的非合作航天器位姿测量方法研究

桂 力,郑顺义,曹姝清,刘宗明,陈 赟

(1.地球空间信息技术协同创新中心，湖北 武汉 430079; 2.武汉大学 遥感信息工程学院,湖北 武汉 430079; 3.武汉大学 电子信息学院,湖北 武汉 430079; 4.上海航天控制技术研究所,上海 201109)

基于点云的非合作航天器位姿测量方法研究

桂 力1、2、3,郑顺义1、2,曹姝清4,刘宗明4,陈 赟4

(1.地球空间信息技术协同创新中心，湖北 武汉 430079; 2.武汉大学 遥感信息工程学院,湖北 武汉 430079; 3.武汉大学 电子信息学院,湖北 武汉 430079; 4.上海航天控制技术研究所,上海 201109)

针对已有基于二维影像的非合作航天器定位定姿方法在目标适应性和稳定性方面的不足，研究了一种基于三维点云的位姿测量方法。提出一种考虑累积误差的参数传递法进行序列点云的配准，用参数传递法获得初始值，在初始值的引导下与基准模型进行快速精确配准，实现了基于实时三维点云的相对运动跟踪，获得了较高的解算精度，方法利用目标的几何形状信息，有更好的普适性和稳健性。分别以仿真模型和现场模型作为测量对象进行位姿跟踪实验，用扫描仪获取动态卫星模型的三维点云并进行位姿解算，测量的运动轨迹与设计值吻合度较好，表明所提方法有较好的稳健性和较高的精度。

非合作航天器； 位姿测量； 三维点云； 点云配准； 累积误差； 三维运动跟踪； 参数传递； ICP算法

0 引言

随着航天技术的飞速发展，对航天器的交会对接、在轨捕获、自动维修等的应用提出了更高的要求。近年来，国内在这些领域的研究取得了进展，如在2011年实现了神舟八号飞船与天宫一号目标飞行器的空间交会对接，这种对接属于大型航天器的合作目标对接，可通过安装主动通信设备及其它特征标志进行识别定位[1]。但针对非合作目标航天器的研究尚不成熟。非合作目标种类繁多，形状各异，对相关技术研究提出了挑战。非合作航天器的空间自主交会和空间在轨服务的研究，首先要解决相对运动过程中的位姿测量问题。目前已有学者进行了大量研究。文献[2]提出了一种利用天文观测图像对卫星及其子部件进行三维姿态估计的方法，主要用于解决地面观测在轨卫星的姿态测量问题；文献[3]根据光流法的基本原理，提出了一种基于特征光流信息的空间非合作目标的相对位姿估计方法，通过STK软件生成的卫星视频验证了算法的可行性。此外，有多位研究者提出了类似的解决方法[4-5]。此类方法的共同点是基于二维影像数据确定三维位姿信息，优点是方便灵活、成本低廉，但在光照等干扰因素的影响下常难以保证测量结果的稳定性。

随着三维扫描仪的出现，目标表面的三维点云数据的获取越来越方便，逐渐出现了基于点云数据的位姿测量方法。文献[6]用一种激光相机系统(LCS)估计运动目标的位姿，实验结果表明在闭环配置下具稳健的位姿跟踪能力；文献[7]针对3D测图提出一种基于平面块的快速配准方法，在3D成图过程中恢复了扫描仪的位姿信息。现有的研究多针对合作目标，如已知目标的CAD数据，或基于某种特定的约束条件，对目标的几何形状有较多的限定。针对非合作目标航天器位姿测量的需求，本文研究了一种与目标形状无关的定位定姿方法，以提高基于点云的位姿测量方法的适应性。该方法根据点云配准的基本方法，给出模型位姿参数的传递模型，提出配准精度的优化方法以提升位姿测量的精度，并用仿真卫星模型数据和现场真实卫星模型数据对本文方法的有效性进行验证，分析了试验结果。

1 点云配准基本原理

两片点云数据间的配准是基于三维点云数据进行位姿测量的研究基础，快速有效完成扫描点的配准对航天器的定位定姿有重要意义，在三维物体识别、基于点云的三维重建等中也有大量的应用。点云数据表达了物体的形状信息，点云配准的基本原理是通过一定的测度和算法使基准点云与待配准点云间达到最佳重合，即实现了三维点间的对应关系。对点云模型的配准问题，已提出了多钟解决方法，如迭代最近点(ICP)算法、点标记法、遗传算法、四点一致集法(4pcs)等[8-11]。这些方法各有优缺点，在某些特定条件下可较好地解决配准问题，但总体来看，ICP算法由于其普适性强，有很高的几何精度，得到了更广泛的应用。

一般来讲，配准问题可简单描述为：对基准模型点Pi(i=1,2,…,n) 和待配准点Qi(i=1,2,…,m)，这两组点云模型是某个刚性目标上有一定重合度的扫描片段，该扫描片段间存在一种旋转、平移的转换关系，通过这种转换可将待配准点云转换至模型点的坐标系中，实现重叠区域的最佳重合。一般用一种目标函数表示这种最佳重合，有

(1)

式中：qj为待配准点中的某点(一般会选取部分点参与计算)；pj为该点对应的基准模型点中的对应点；F为一种测度函数，依据对应点作为参数，以旋转矩阵R和平移向量T为未知数，通过使用某种“距离”准则计算每对对应点间的数值，当所有数值的平方和最小时即为待求问题R，T的当前解。但实际上其中的对应点是随R，T而变的，每解算完一次后重新选取对应点再次计算，直至达到最终的收敛条件。

点云模型配准的基本步骤如图1所示。整个处理过程基本包括：数据预处理、对应点求取、参数解算、收敛性判断、待配准模型更新等。其中求取对应点和解算参数属于循环迭代过程，随每次计算的参数R，T逐渐趋于合理，待配准模型将越来越接近于基准模型，以此达到解算最终参数的目的。

图1 模型配准计算流程Fig.1 Flowchart of model registration calculation

2 基于点云的定位定姿方法

2.1 模型位姿参数传递

以某时刻航天器所在位置为参考基准，以该时刻获得的航天器三维点云数据为基准模型，在运动过程中通过实时运动位姿跟踪的方法，关联相邻点云帧间的位姿并进行参数传递计算，则可获得当前三维点云相对基准模型的位置姿态信息，实现非合作航天器的定位定姿。

用上述两片点云间的配准方法可确定运动过程中每次扫描的当前点云数据与相邻点云间的位姿关系，其与基准点云间关系的确定方法如下。

设从第一帧点云至第N+1帧点云的序号分别为0，1，2，3，…，N，根据点云配准的几何关系，两片点云(qN,pN)间有满足变换关系

qN=R×pN+T.

(2)

则对N+1片点云，用X0,X1,…,XN表示点云模型，则XN到XN-1的转换参数为RN，TN(N>0)，成立

(3)

由式(3)间的传递关系可得点云N传递至点云0的计算公式为

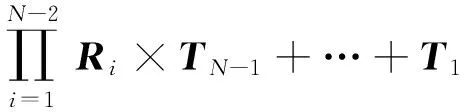
(4)

式(4)化简可得

(N>0,中间式当N>1时存在).

(5)

式(5)即为模型位置姿态的传递公式。

为便于编程计算，还可用另一种方式表达位置姿态的传递，即对P，Q两片点云，将参数矩阵R，T写成齐次型后，则变换公式为

(6)

用R表示中间的变换矩阵，则第N帧点云数据至基准帧数据间的变换关系可表示为

X0=R1×R2…RN×XN.

(7)

式中R的表达涵盖了位置、姿态参数，形式更简洁，也便于编程使用。

上述公式即确定了某时刻获得的三维点云数据与基准点云数据的变换关系。由于扫描得到的序列点云间具很大的时空相关性，两片相邻点云间差异性很小，直接得到的三维点云数据已有较好的配准初始值。故使用每次获得的点云与其上一帧点云进行配准，能快速获得较好的配准结果。然后再由参数传递公式得到当前帧与基准帧间的变换关系，最终可获得基准模型坐标系中的解算结果。

2.2 配准精度优化

通过点云配准参数的传递计算，在得到相邻两片点云间的位置姿态条件下可完成任意点云至参考系的计算。但实际试验中常发现当点云数量累积较多时，通过参数传递计算得到的结果会存在一定的系统误差，该误差随跟踪次数增加而增大。误差主要源于仪器自身误差、噪声点云误差、目标的几何结构导致的配准误差等，在两两配准时点云间的误差很小，对结果的影响不大，但当累积计算时，所有配准的误差都会参与计算，产生了误差传播，故扫描的次数越多累积误差就越大。对这种误差的累积传播问题已有文献进行了分析，给出了严格的误差传播模型，从该模型可知初始的配准误差会随配准过程进行传递[12-13]。

由上述分析知：该误差主要由参数的传播过程产生，如采取适当方法对传播过程进行优化，就能最大程度消除该误差的影响。综合考虑配准速度和精度，本文采用一种参数传递和精确配准结合的方法，流程如图2所示。

图2 点云精确配准流程Fig.2 Flowchart of precise point cloud registration

配准精度优化计算主要步骤为：

a)对采集的最新帧点云数据N，与第N-1帧的点云数据进行配准。由于相邻两帧间差异性很小，该配准步骤能快速完成。

b)用基于模型位置的参数传递法求得当前点云帧数据相对基准模型的位姿参数，以该参数作为配准的初始值，将当前点云帧变换至基准模型所在坐标系中。通过此变换能保证待配准点云与基准模型间差异最小化，利于配准的收敛。

c)将变换后的当前点云帧与基准模型进行快速配准，获得精确的配准结果。将配准参数与初始参数进行合并，即得到第N帧点云到基准模型间的位姿信息，完成了坐标系的统一。

d)采集下一帧点云数据，记N=N+1，继续重复上述步骤。

通过上述步骤，完成了序列点云数据的精确配准。上述算法中完成了两次点云配准过程：与前一帧相邻点云配准及与基准模型的配准。由于序列点云数据的空间连续性，相邻点云帧间有较高的一致性，能很快完成配准；在较准确的初始值引导下，待配准点云亦能快速完成与基准模型的配准。该算法巧妙利用了序列点云间的时空连续性，用参数传递方法获得与基准模型配准的初始值，保证了配准的收敛性和精确性。实际应用中，若相对运动缓慢，在小时空范围内输入的序列点云量必然增多，点云间一致性更大，可间隔一段时间获取一帧进行处理，或直接以第N-1帧的配准参数作为初始值引导第N帧点云与基准模型进行配准，也能获得较好的效果。

在误差传播过程中，扫描仪自身的位置精度和指向精度也非常重要。两种精度在实际使用时又可分为绝对精度和相对精度，决定这两种精度指标的误差因素有系统误差、检校误差和偶然误差等。一般可用通过差分运算抵消相同影响因素，所得相对精度将远高于绝对精度，故在本文研究的求相对位姿关系问题中，相对位姿的误差对最终的位姿测量精度影响较小。由模型位姿参数解算的参数传递法到配准精度的优化方法，考虑了由相对目标的位置精度和对目标探测的指向精度及其它因素引起的配准误差累积问题，用优化配准方法可消除这种误差累积的影响。

3 实验与分析

3.1 实验环境

为验证本文所提方法的有效性，用微软Kinect扫描仪进行数据扫描和算法测试，Kinect扫描仪采用“体编码”技术，根据散斑投影在不同深度会形成不同的图案原理，利用拍摄得到的散斑图案与事先标定的图案进行相关处理，可快速获得照片的深度信息，从而得到被扫描目标表面的完整点云。

用该设备进行三维点云扫描。先将其放置在某较平稳的平台上作为主动方，控制平台运动以模拟主动方与被扫描对象间的相对运动过程。在本文实验中，将先针对仿真卫星模型进行定性实验分析，再用现场卫星模型在有运动轨道约束条件下进行定性与定量的分析。

3.2 仿真卫星模型实验结果与分析

仿真中用简易材料设计了一个卫星模型，如图3(a)所示。该模型由主面板、圆形天线、载荷等组成，具备一般卫星模型的特征。Kinect扫描仪置于一个易推拉的物体上，由人工推拉该物体带动扫描仪运动，以模仿主动方与卫星目标间的相对运动。实验中，设计了主动方由远至近、由近至远的多个来回的运动路线，并在每次运动过程中人工控制其行走路线尽可能保持直线，以验证实验效果。

图3 仿真卫星模型实验结果Fig.3 Experimental results of simulation satellite model

通过将Kinect扫描仪与PC机相互连接，由自主开发的位姿测量软件实时获取扫描仪的点云数据，用本文算法解算运动过程中的相对位姿信息，结果如图3(b)所示。图3(b)中：为显示解算出的所有位姿参数在空间中的可视化效果，用红绿色三维线框表达了当前位置与姿态信息。由图3(b)可知：所有的位置朝向较一致，表明运动跟踪过程中在方向上无大的变化，这与实际的运动情况一致。将所有的位置点连接起来，形成图中的黄色轨迹线，由轨迹线的走势可发现：整个运动过程呈现为数条往返的直线状，符合实际实验中设计的来回走动路线。待配准点完成配准后与基准模型的叠加效果如图3(c)所示。图3(c)中：蓝色点为基准模型；绿色点为待配准点。由点云叠加结果可知：两者能较准确地重合，表明配准精度较高。

3.3 现场卫星模型实验结果与分析

仿真实验测试从定性的角度说明了本文方法定位定姿有效性。为进一步分析位姿测量的精度，本文用某实验室现场卫星模型进行了另一组实验。该组实验使用一种精确制作的卫星模型，在该实验室现场设计了一种高精度直线导轨，导轨末端正对该卫星模型，导轨上安置有可控制移动的运动平台，将扫描仪置在于运动平台上，控制其由近至远进行运动以模拟空间目标的相对运动过程。在本实验中，由于导轨设计为直线状，整个运动过程将严格在直线性约束下进行，为实验结果的精确分析提供了依据。

现场卫星模型在一个序列运动过程中的实验结果如图4所示。从图4(b)可知：卫星相对运动参数形成的轨迹在空间呈现为一条很严格的直线，与导轨控制运动的实验设计相符，表明位置信息得到较好恢复；所有位置的朝向一致，表明姿态信息恢复良好。变换后的待配准点云与基准点云叠加效果较佳(图4(c))，也反映了测量精度较高。

图4 现场卫星模型实验结果Fig.4 Experimental results of field satellite model

进一步可更精确地分析位姿参数的精度。因实验过程中在直线轨道上行走，方向都是一致的，则可认为运动位置轨迹满足直线模型，运动姿态全局一致。将运动过程中解算的位置参数用数值可视化方式显示，结果如图5所示。由图5可更精确地观察到整个运动过程中所有空间点呈现直线状，这与图4(b)的结果相互印证。使用直线模型，用最小二乘法对空间三维位置进行三维直线拟合，所得空间直线如图6所示。由图6可认为该直线为轨迹的真值位置。

图5 位姿测量轨迹Fig.5 Trajectory of POS measurement

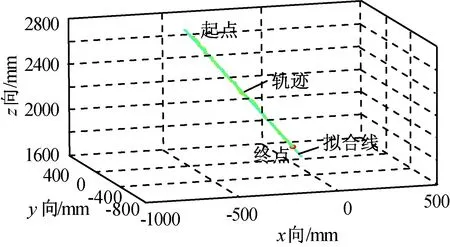
图6 位姿数据拟合空间直线结果Fig.6 3-D line fitting result of POS data

为分析位置的精度，对某个空间位置点，计算该点至真值直线最近的点作为其参考真值，然后将该空间位置点的X，Y，Z三轴位置分量分别与参考真值进行差值计算，可得当前空间位置点误差的三个分量。部分测量序列的X，Y，Z分量误差分布如图7所示。由图7可知：位置量整体分布较一致，无大的跳跃现象，表明其稳定性较佳；最大误差不超过4 mm，表明位置精度较高。

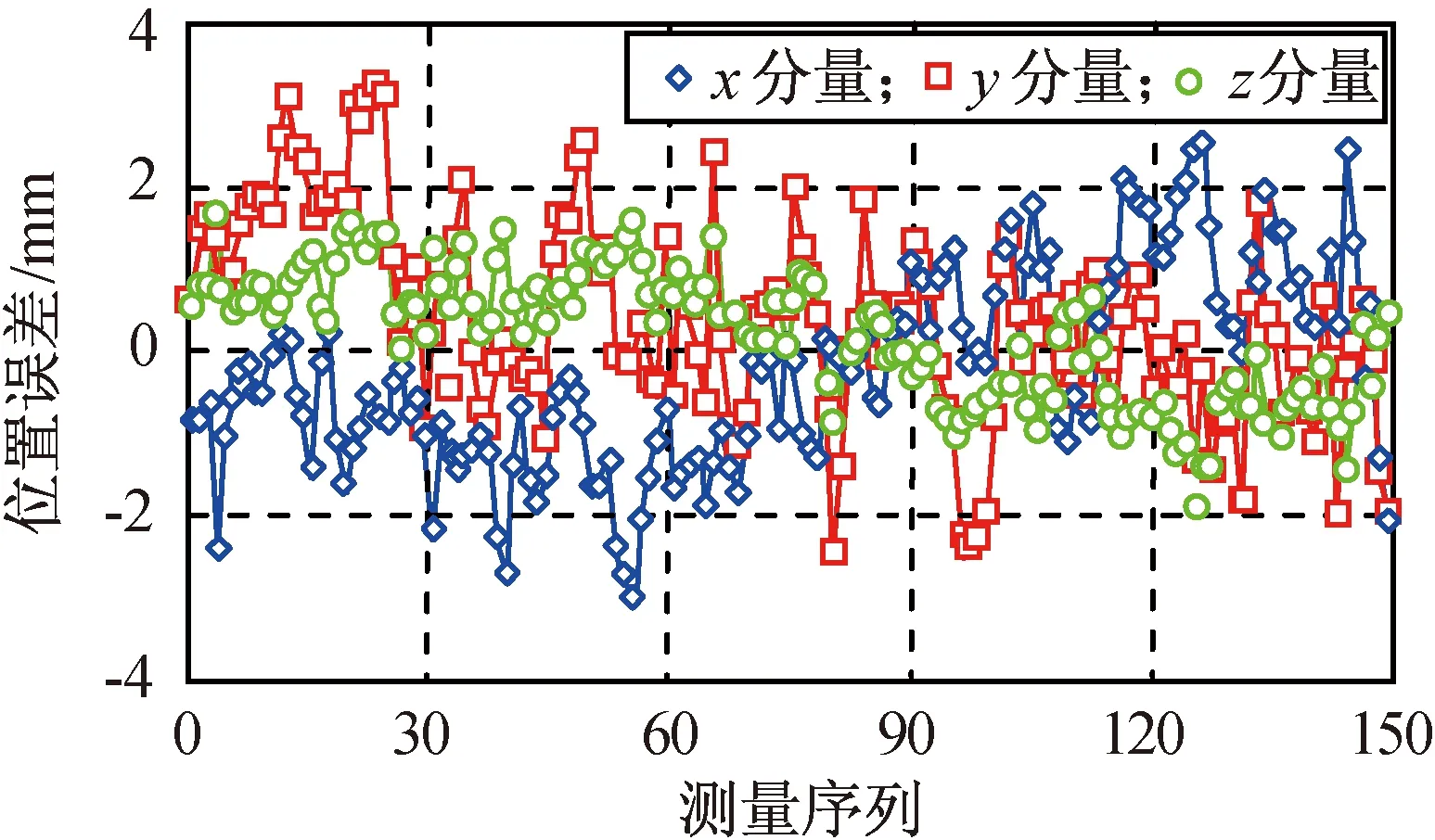
图7 位置分量误差分布Fig.7 Error distribution of position components

对角度精度，为测量角度的真值，实验设计中保持扫描仪与被扫描目标在三个角度分量上均无旋转变动，即全局角度信息保持一致，因此可取所有解算出的角度值的平均值作为真值。将三个角度分量分别与该真值进行差值计算，可得各角度分量的误差量，其中三个角度分量的误差分布如图8所示。由图8可知：角度误差量均较小，最大偏差不大于0.15°，能满足实际应用需求。

图8 角度分量误差分布Fig.8 Error distribution of angle componets

4 结束语

本文针对非合作航天器相对运动过程中位姿测量问题，提出了一种基于点云配准和参数精确传递的位姿测量方法。用扫描仪仿真获取非合作航天器点云数据进行测量，仿真实验结果和现场实验结果均表明本文方法有较好的稳定性和较高的精度，能满足实际应用需求。因本文方法无需事先获取被测量目标的几何信息，故对各类非合作目标航天器都具有适应性。已有的基于影像的定位定姿方法常要求目标具有某些已知的形状或纹理信息，普适性不强，且易受光照等的影响，其结果往往会产生较大的跳跃，稳定性不佳。相比之下，基于点云的方法能较好地利用目标的几何信息，具更好的适应性和稳定性。另一方面，相对已有的依赖于特征提取方法，本文方法能用于更多种类的航天器的位姿测量，不要求目标本身具备任何特殊的标识，可自适应地利用目标自身的几何特征进行测量，无需对目标进行特殊处理，故也可用于未知目标的定位定姿，应用范围更广。由于受限于硬件，目前点云数据的获取还无法如影像那样对远距离目标进行成像，本文方法的使用距离将可能受到硬件的限制，后续研究中可考虑结合两者的优点组合使用，以进一步提高实际应用中可测量的距离。

[1] 李隆球, 张广玉, 柏合民, 等. 非合作目标卫星三臂型对接机构及其力学分析[J]. 上海航天, 2015, 32(1): 5-11.

[2] 魏小峰, 耿则勋, 娄博, 等. 空间目标三维姿态估计方法[J]. 武汉大学学报(信息科学版), 2015, 40(1): 96-101+111.

[3] 程文华, 姚红, 张雅声. 基于特征光流信息的空间非合作目标相对位姿估计[J]. 上海航天, 2015, 32(5): 9-14.

[4] 张剑清, 张春森, 贺少军. 双目序列影像三维运动参数确定[J]. 武汉大学学报(信息科学版), 2006, 31(1): 43-46.

[5] 周军, 白博, 于晓洲. 一种非合作目标相对位置和姿态确定方法[J]. 宇航学报, 2011, 32(3): 516-521.

[6] AGHILI F, KURYLLO M, OKOUNEVA G, et al. Robust pose estimation of moving objects using laser camera data for autonomous rendezvous and docking[C]// In Proceedings of the International Society of Photogrammetry and Remote Sensing Archives. Paris: [s. n.], 2009: XXXⅧ-3/W8, 253-258.

[7] PATHAK K, BIRK A, VAKEVIIUS N, et al. Fast registration based on noisy planes with unknown correspondences for 3-D mapping[J]. IEEE Transactions on Robotics, 2010, 26(3): 424-441.

[8] BESL P J, MCKAY N D. A method for registration of 3-D shapes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1992, 14(2): 239-256.

[9] 梁云波, 邓文怡, 娄小平, 等. 基于标志点的多视三维数据自动拼接方法[J]. 北京信息科技大学学报(自然科学版), 2010, 25(1): 30-33.

[10] SILVA L, BELLON O R P, BOYER K L. Precision range image registration using a robust surface interpenetration measure and enhanced genetic algorithms[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(5): 762-776.

[11] MELLADO N, AIGER D, MITRA N J. Super 4PCS fast global pointcloud registration via smart indexing[C]// Computer Graphics Forum. [S. l.], [s. n.], 2014, 33(5): 205-215.

[12] 程效军, 施贵刚, 王峰, 等. 点云配准误差传播规律的研究[J]. 同济大学学报(自然科学版), 2009, 37(12): 1668-1672.

[13] 徐源强, 高井祥, 张丽, 等. 地面三维激光扫描的点云配准误差研究[J]. 大地测量与地球动力学, 2011, 31(2): 129-132.

Research of Pose and Altitude Measurement for Non-Cooperative Spacecraft Based on 3D Point Clouds

GUI Li1, 2, 3, ZHENG Shun-yi1, 2, CAO Shu-qing4, LIU Zong-ming4， CHEN Yun4

(1. Collaborative Innovation Center of Geospatial Technology, Wuhan 430079, Hubei, China; 2. School of Remote Sensing and Information Engineering, Wuhan University, Wuhan 430079, Hubei, China; 3. School of Electronic Information, Wuhan University, Wuhan 430079, Hubei, China; 4. Shanghai Institute of Spaceflight Control Technology, Shanghai 201109, China)

To solve the problem that existing methods of estimating of the pose for non-cooperative spacecraft based on 2-D images have the disadvantage of poor adaptability and instability for variant spacecraft, a pose and altitude (POS) measurement method is researched, which can make full use of shape information for objects and lead to better versatility and robustness. A method of parameter transfer with considering of the error accumulation problem was proposed for sequential point clouds registration in this paper. An initial value with parameter transfer algorithm was got firstly. And then a registration with base model was made quickly by the initial value. This method leads to a result of tracking with relative movement based on real-time scanning 3-D point clouds and a high accuracy is achieved in pose and altitude measurement. Using simulation satellite model and field satellite model apart for pose tracking experiments, a series of satellite model point clouds with a 3-D point scanner and solving the results when scanning were carried on. The results showed that the measured trajectory was consistent with the designed trajectory, which meant that the method proposed in this paper was robust and high accuracy.

Non-cooperative spacecraft; Pose and altitude measurement; 3D point clouds; Point cloud registration; Accumulative error; 3D motion tracking; Parameter transfer; Iterative closest point algorithm

1006-1630(2016)06-0122-07

2016-06-13；

2016-11-29

中央高校基本科研业务费专项资金资助(2042016kf0012)；上海航天科技创新基金资助(SAST201446)

桂 力(1986—)，男，助理研究员，主要从事计算机视觉研究。

V448.21

A

10.19328/j.cnki.1006-1630.2016.06.018