大跨度椭圆抛物面弦支穹顶结构的缺陷敏感区域分析*
2016-02-14姜正荣石开荣刘红亮蔡健罗斌
姜正荣 石开荣† 刘红亮 蔡健 罗斌
(1.华南理工大学 土木与交通学院, 广东 广州 510640; 2.华南理工大学 亚热带建筑科学国家重点实验室,广东 广州 510640; 3.东南大学 土木工程学院, 江苏 南京 210096)
大跨度椭圆抛物面弦支穹顶结构的缺陷敏感区域分析*
姜正荣1,2石开荣1,2†刘红亮1蔡健1,2罗斌3
(1.华南理工大学 土木与交通学院, 广东 广州 510640; 2.华南理工大学 亚热带建筑科学国家重点实验室,广东 广州 510640; 3.东南大学 土木工程学院, 江苏 南京 210096)
厚街体育馆钢屋盖采用大跨度椭圆抛物面弦支穹顶结构,支座间净跨110 m×80 m,上部单层网壳矢高9.4 m.分别以此结构与相应的单层网壳为分析对象,采用改进的随机缺陷模态法,对两类结构的缺陷敏感区域进行对比研究.在此基础上,进一步探讨局部拓扑形式改变及活载半跨分布对弦支穹顶结构缺陷敏感区域的影响.研究表明:弦支穹顶结构的缺陷敏感区域位于上部单层网壳;弦支穹顶与相应单层网壳的缺陷敏感区域有较大差异,下部索杆体系的引入明显改善了上部单层网壳的缺陷敏感性;局部拓扑形式的改变,可有效降低结构的缺陷敏感程度;活载的半跨分布对传统拓扑形式弦支穹顶结构缺陷敏感区域的影响并不大,但对于该结构上部单层网壳中心区域的影响较为显著.
弦支穹顶;单层网壳;稳定性;随机缺陷模态法;缺陷敏感区域
弦支穹顶[1- 2]是由上部单层网壳和下部索杆体系组合而成的新型杂交空间结构体系,相比于传统的单层网壳,其矢跨比更小,跨越能力更强.目前对弦支穹顶结构缺陷稳定性的研究主要侧重于缺陷大小和分布的模拟以及缺陷对结构稳定承载力的影响[3- 6],对结构缺陷敏感区域的研究相对较少[7- 9].
结构的初始缺陷包括节点位置的安装偏差、杆件的初弯曲、初偏心等.其中,安装偏差是与结构整体有关的初始几何缺陷,而初弯曲、初偏心为杆件自身的缺陷.结构的初始缺陷不可避免,这是因为:一方面,由于节点安装偏差引起的初始几何缺陷不能完全消除,只能控制在一定范围内;另一方面,由于加工制作的精度所限,杆件的初弯曲、初偏心等无法规避.但是,在对结构进行稳定性分析时,所有杆件都应经过设计,并验算其承载力和压杆的稳定性,故杆件的初始缺陷对结构整体稳定性的影响应受到限制[10].因此,下文分析主要考虑节点位置的安装偏差.
缺陷敏感区域是指结构中对初始几何缺陷最为敏感的区域.工程实践中,弦支穹顶结构往往呈现出跨度大、节点数量多的特点,施工过程中若能根据结构不同区域相对缺陷的敏感程度,对其节点安装偏差采用不同的质量控制标准,则可减少现场工作量,提高工程经济性.
文中以笔者主持设计的东莞厚街体育馆弦支穹顶屋盖为研究对象,采用通用有限元程序Ansys对其进行缺陷敏感区域分析,揭示其不同区域对初始几何缺陷的敏感程度,并将弦支穹顶与相应单层网壳的缺陷敏感区域进行对比,探讨局部拓扑形式及活载半跨分布对弦支穹顶结构缺陷敏感区域的影响.
1 分析模型
厚街体育馆钢屋盖采用椭圆抛物面稀索体系弦支穹顶结构,平面为椭圆形(127.875 m×93 m),其中支座间净跨110 m×80 m(见图1(a)),支座外围悬挑部分通过V型斜杆与相应标高的钢圈梁侧边相连.上部单层网壳矢高9.4 m,相对于结构净跨,长、短轴矢跨比分别为1/11.7及1/8.5(见图1(b)、1(c)).上部单层网壳采用联方型+凯威特型的混合网格布置,其中在屋盖中心区域,为兼顾建筑美观和采光要求,设计为绽放的花瓣状网格(见图1(d)).下部索杆体系由4圈环向索、径向钢拉杆及撑杆组成,对应于单层网壳的第3、5、7、9圈环向杆(图1(a)、1(e)).撑杆上、下端均采用铸钢节点,其他部分采用圆管相贯节点.屋盖沿110 m×80 m椭圆线支承在钢圈梁顶,设固定铰支座共24个,支座采用焊接空心球,球中标高22.600 m.


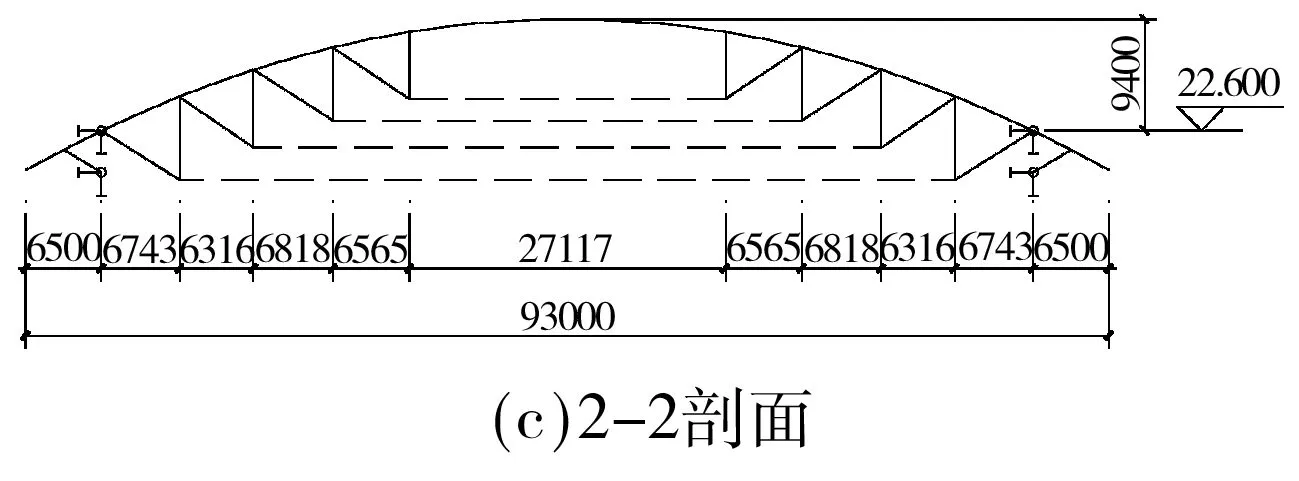
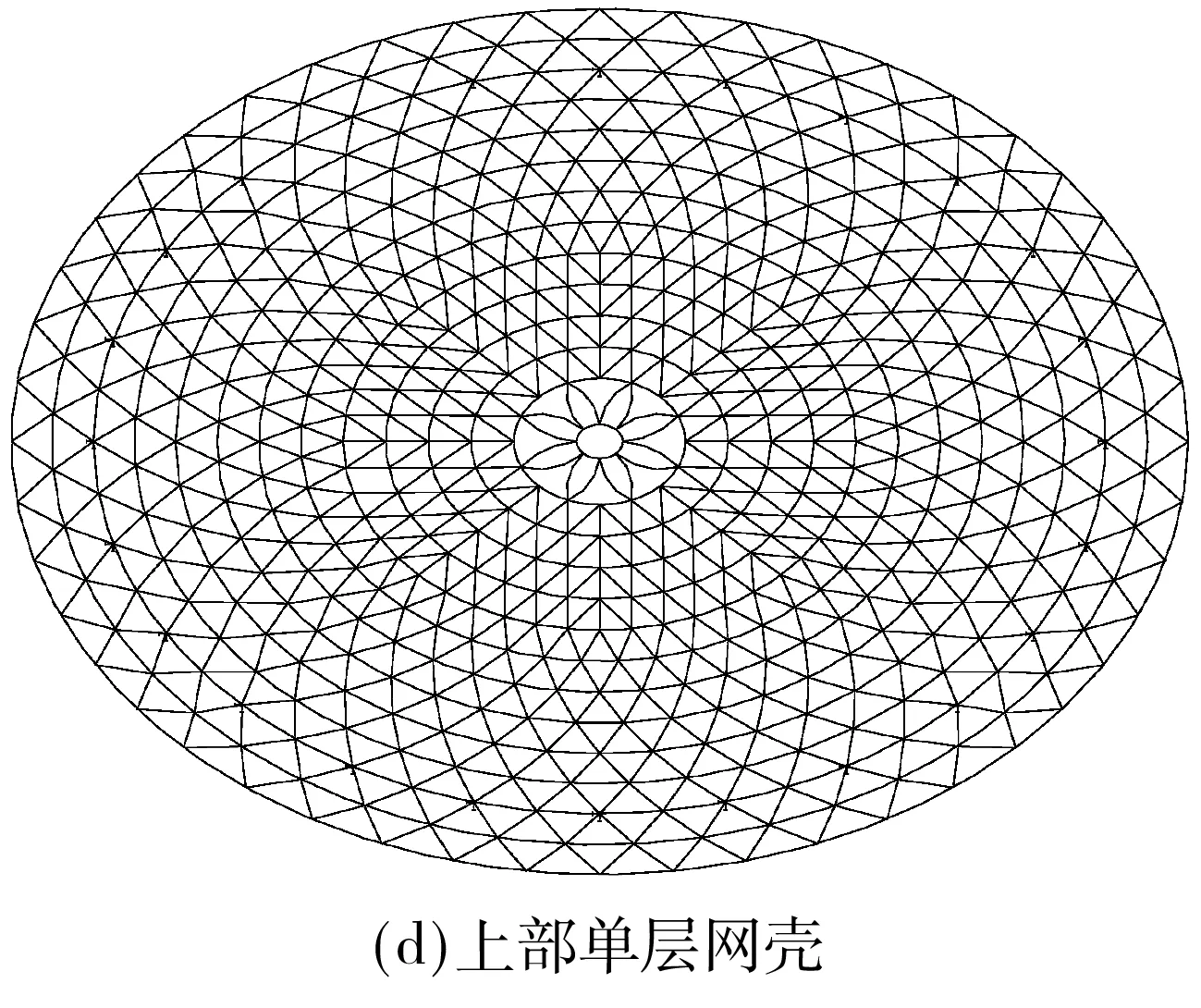

图1 分析模型(单位:mm)Fig.1 Analytical model(Unit:mm)
构件和材料规格见表1.
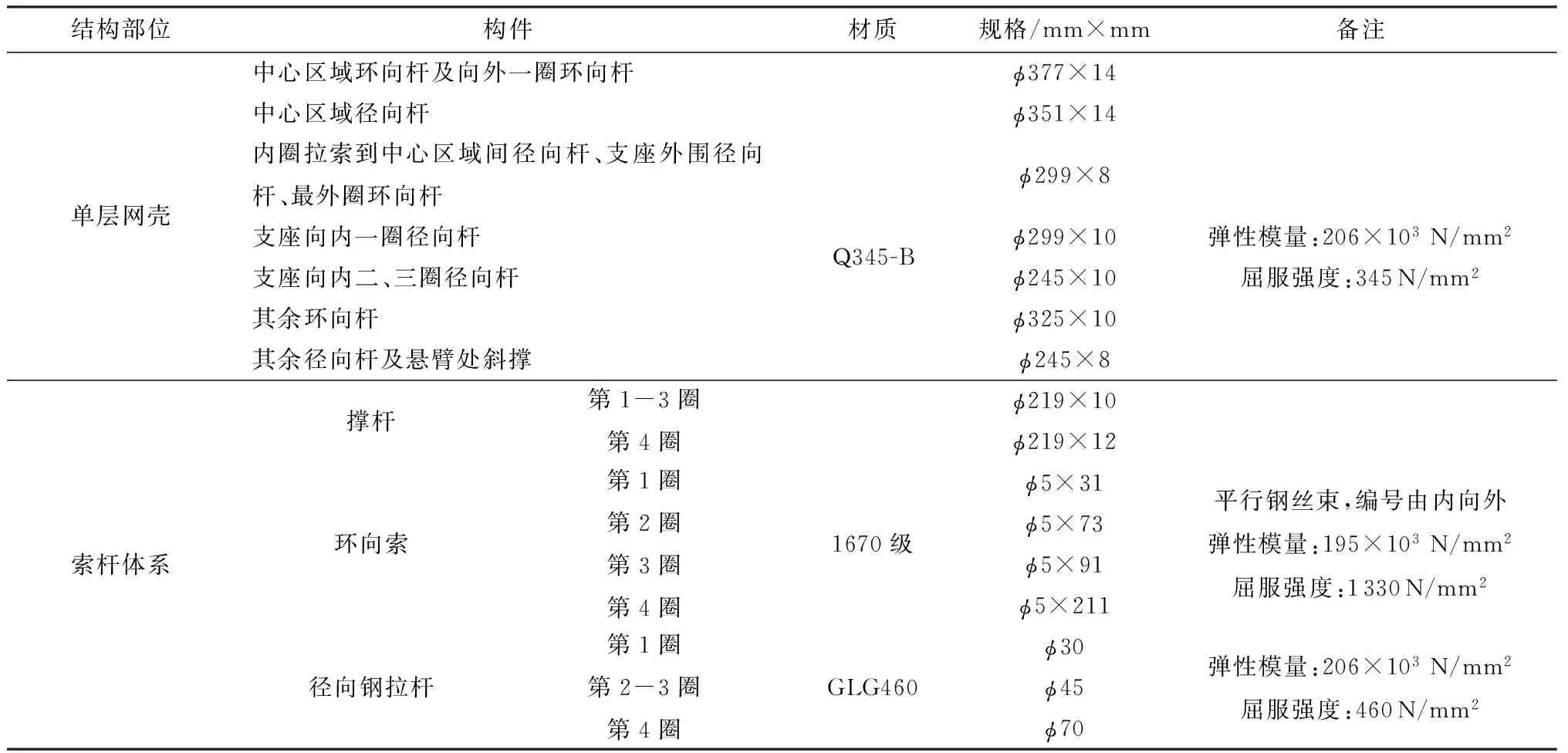
表1 构件和材料规格Table 1 Specifications of components and materials
屋面恒载如下:单层网壳中心28 m×20 m椭圆区域为0.8 kN/m2,其余区域为0.5 kN/m2;根据马道布置,部分节点考虑了马道及作用在其上的附加吊重传来的集中荷载;构件自重由程序自动计算,并将撑杆的重力密度按比例放大,以考虑其上下端铸钢节点自重.不上人屋面活载为0.3 kN/m2,考虑满布、半长轴(图2(a))、半短轴(图2(b))3种分布情况.由内向外各圈环向索初始预拉力分别为:404.2、681.1、1 008.4、1 584.4 kN[11].

图2 活载布置Fig.2 Layouts of live loads
Ansys分析时,环向索及径向钢拉杆采用只拉LINK10单元模拟,撑杆以LINK8单元模拟,上部单层网壳杆件以BEAM189单元模拟,采用初应变模拟环向索的初始预拉力.单层网壳节点刚接,撑杆与单层网壳的连接为铰接.
2 分析原理及步骤
2.1 非线性屈曲分析
特征值屈曲分析通常会过高估计结构的稳定承载力,其计算结果一般不能直接用于工程设计,且无法反映结构的荷载-位移全过程工作性能.为了更好地研究结构屈曲前后的性能,需对结构进行基于大挠度理论的非线性屈曲分析,其控制方程如下:
KTΔU=ΔP-F
(1)
式中,KT为切线刚度矩阵,ΔU为位移增量向量,ΔP为等效外荷载向量,F为等效节点力向量.
对于式(1)的求解,各种改进的弧长控制方法被认为是跟踪屈曲路径全过程最有效的方法[12].若考虑材料弹塑性的影响,切线刚度矩阵表达式的变化详见文献[13]中的相关表述.目前,考虑几何及材料非线性的荷载-位移全过程分析方法已较为成熟,为更加准确地反映结构实际工作状况,有必要对结构进行考虑双重非线性的全过程分析.因此,下文分析均考虑材料弹塑性的影响,并考虑以下3种组合:1.0恒载+1.0满布活载(组合1);1.0恒载+1.0半长轴均布活载(组合2);1.0恒载+1.0半短轴均布活载(组合3).
2.2 改进的随机缺陷模态法
从概率统计的角度分析,各种因素导致的节点安装偏差应近似地符合正态分布.在此假设各节点安装偏差并不相互影响,互相独立,即每个节点位置的偏差随机变量为RX/2,随机变量X服从标准正态分布.R为最大安装偏差,文中取结构短轴跨度的1/300.为提高计算效率,采用改进的随机缺陷模态法引入结构的初始几何缺陷,即通过分布拟合检验来判断样本数量n的大小[8].
分析方法:生成服从正态分布的节点安装偏差;引入上述偏差后,对结构进行非线性屈曲分析,获得稳定承载力系数作为样本;进行n次分析,直到样本能够通过分布拟合检验.假设总体X的分布未知,x1,x2,…,xn是来自X的样本值,然后检验假设:①H0:总体X的分布函数为F(x);②H1:总体X的分布函数不是F(x).
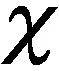
(2)
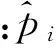
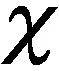
2.3 分析步骤
结构的缺陷敏感区域分析采取以下步骤:
(1)对无缺陷理想结构进行双重非线性屈曲分析,获得稳定承载力系数K;
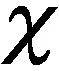
(3)令βi=(K-Ki)/K×100%,βi为缺陷敏感系数,其值越大,则表示该区域节点对缺陷越敏感,故βi最大的节点区域即为结构的缺陷敏感区域.
3 缺陷敏感区域分析
3.1 样本数量的确定原则
随机缺陷模态法中,样本数量越多则样本分布越接近总体分布,样本参数与总体参数的差距也就越小.因此,首先需确定样本数量,在保证足够精度的条件下尽可能地减少计算工作量.理论上,样本数量n≥50即可,现分别取样本数量为50、100、150、200进行分析.为此,借鉴文献[14]的研究思路,首先考虑组合1作用下,仅在结构上部单层网壳中引入初始几何缺陷进行分析,样本数量取值的影响见表2.

表2 样本数量取值的影响1)Table 2 Influence of sample size
1)显著性水平α=0.05.
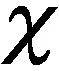
3.2 弦支穹顶结构分析结果
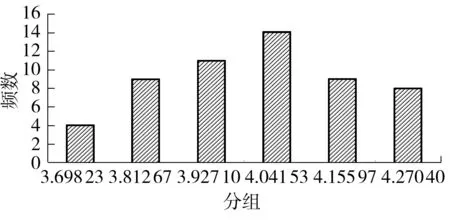
图3 样本直方图Fig.3 Sample histogram
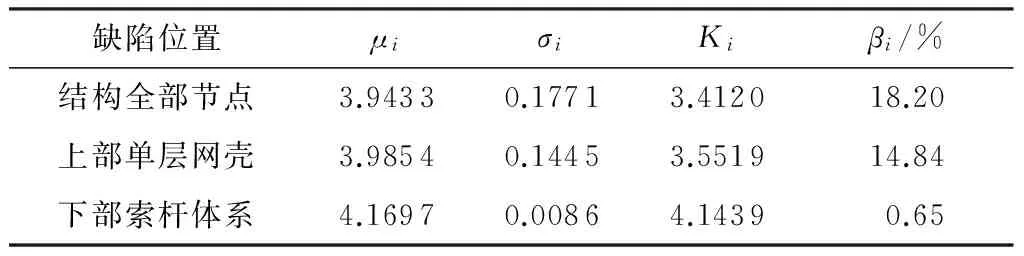
表3 缺陷敏感系数对比1)Table 3 Comparison of imperfection sensitive coefficient
1)组合1作用下无缺陷结构的稳定承载力系数K=4.171.
由表3可见,组合1作用下,分别在上部单层网壳及下部索杆体系中引入初始几何缺陷,计算所得βi值差异较大.相比于下部索杆体系,上部单层网壳对初始几何缺陷更为敏感.在结构全部节点中引入初始几何缺陷所得稳定承载力系数为3.412 0,与仅在上部单层网壳中引入初始几何缺陷所得结果3.551 9相比,相差3.94%,颇为接近.由此说明,该结构的缺陷敏感区域位于上部单层网壳,而下部索杆体系对缺陷的敏感程度很低.工程实践中,对类似结构进行非线性屈曲分析时,为减少计算工作量,建议仅在上部单层网壳中引入初始几何缺陷,即可满足工程精度要求.因此,下文出现“全部节点”均指上部单层网壳全部节点.组合1作用下,弦支穹顶上部单层网壳缺陷敏感区域的具体位置和影响程度见表4.
表4 组合1作用下上部单层网壳的缺陷敏感区域
Table 4 Imperfection sensitive region of upper single layer reticulated shell under load combination 1
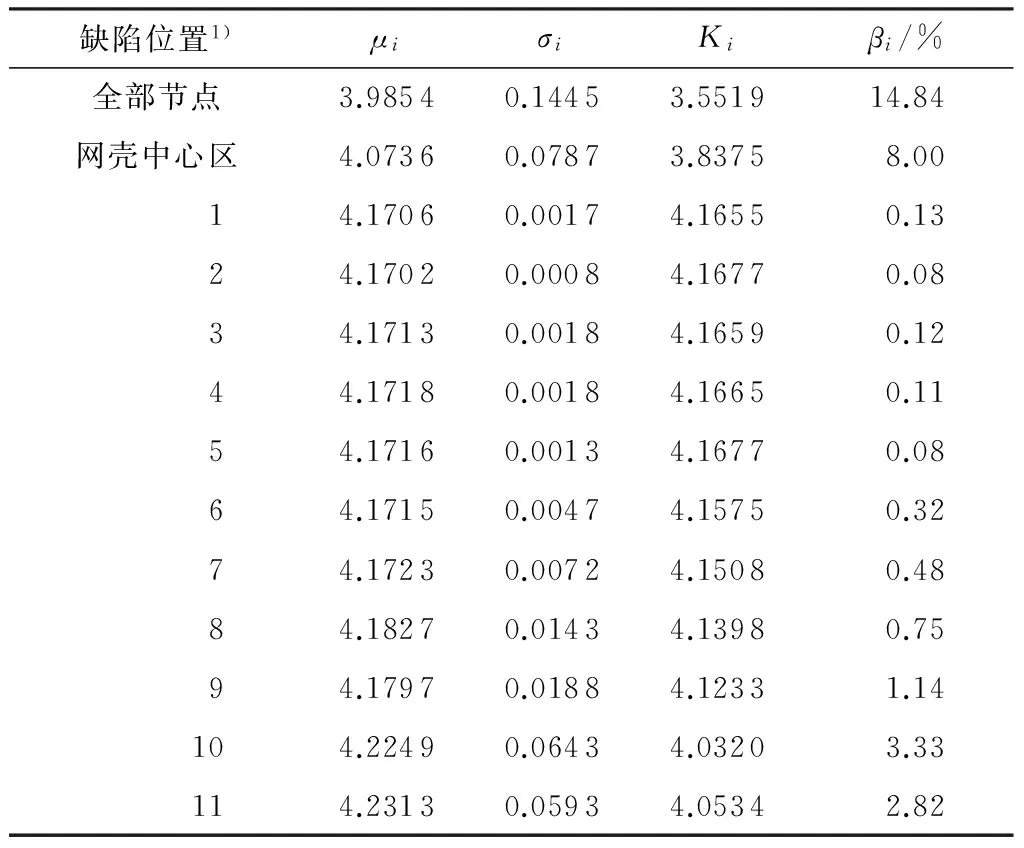
缺陷位置1)μiσiKiβi/%全部节点3.98540.14453.551914.84网壳中心区4.07360.07873.83758.0014.17060.00174.16550.1324.17020.00084.16770.0834.17130.00184.16590.1244.17180.00184.16650.1154.17160.00134.16770.0864.17150.00474.15750.3274.17230.00724.15080.4884.18270.01434.13980.7594.17970.01884.12331.14104.22490.06434.03203.33114.23130.05934.05342.82
1)“缺陷位置”列中,1-11分别指第1-11圈环杆,详见图1(a),余同.
缺陷敏感系数βi可直观地显示上部单层网壳不同区域对缺陷的敏感程度.由表4可知,在单层网壳中心区引入初始几何缺陷,βi为8.00%,支座附近区域(第10~11圈环杆处)对应的βi为3%左右,其他区域的βi均很小.由此说明,该结构的缺陷敏感区域主要位于上部单层网壳中心区,支座附近区域(第10~11圈环杆处)对缺陷的敏感程度次之.而当分别在第1-8圈环杆节点中引入初始几何缺陷时,其稳定承载力系数相对于无缺陷结构的降幅均小于1%,可见这些区域对初始几何缺陷的敏感程度非常低.鉴于此,工程施工过程中,相关单位应在上部单层网壳中心区及支座附近区域采取更严格的质量控制标准,提高制作和安装精度,尽量减小这些区域的节点位置偏差.
3.3 与相应单层网壳的对比
为比较弦支穹顶与相应单层网壳(仅去除下部索杆体系,其他条件均保持不变)缺陷敏感区域的异同,在上文分析的基础上,将弦支穹顶与相应单层网壳进行对比研究,以此探讨下部索杆体系的引入对结构缺陷敏感性的改善程度.组合1作用下相应单层网壳缺陷敏感区域的分析结果见表5.
表5 组合1作用下相应单层网壳的缺陷敏感区域1)
Table 5 Imperfection sensitive region of corresponding single layer reticulated shell under load combination 1
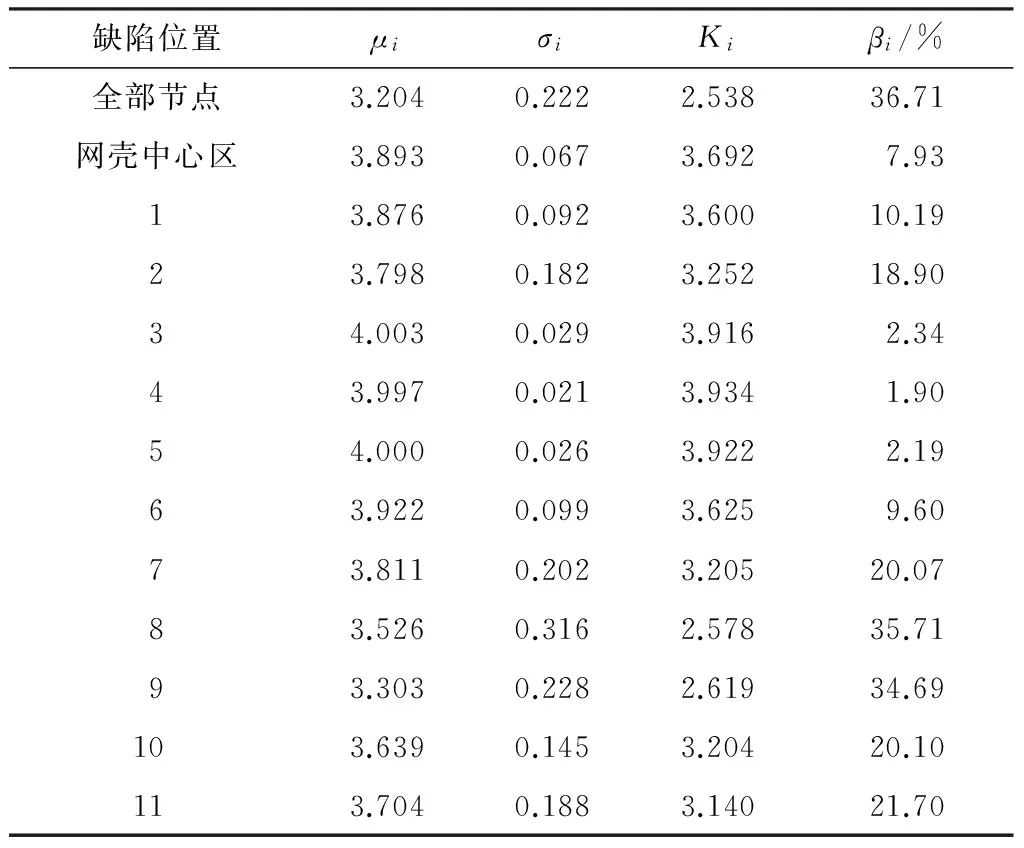
缺陷位置μiσiKiβi/%全部节点3.2040.2222.53836.71网壳中心区3.8930.0673.6927.9313.8760.0923.60010.1923.7980.1823.25218.9034.0030.0293.9162.3443.9970.0213.9341.9054.0000.0263.9222.1963.9220.0993.6259.6073.8110.2023.20520.0783.5260.3162.57835.7193.3030.2282.61934.69103.6390.1453.20420.10113.7040.1883.14021.70
1)组合1作用下无缺陷结构的稳定承载力系数K=4.010.
由表5可见,相应单层网壳的缺陷敏感区域主要位于第7-11圈环杆区域及网壳中心区至第2圈环杆区域.βi越大则缺陷敏感程度越高,对比表5和表4,相应单层网壳的第7-11圈环杆之间区域的βi值均超过20%,最大达35.71%,而在弦支穹顶结构的同一区域,βi最大仅3.33%.
图4列出了弦支穹顶和相应单层网壳不同位置的βi值对比.可以发现,相应单层网壳对缺陷的敏感程度远高于弦支穹顶,尤其是在第7-11圈环杆之间区域.由此说明,弦支穹顶与相应单层网壳的缺陷敏感区域有较大差异,且其影响范围和敏感程度均小于相应的单层网壳.究其原因,在于下部索杆体系的引入明显改善了上部单层网壳的缺陷敏感性.
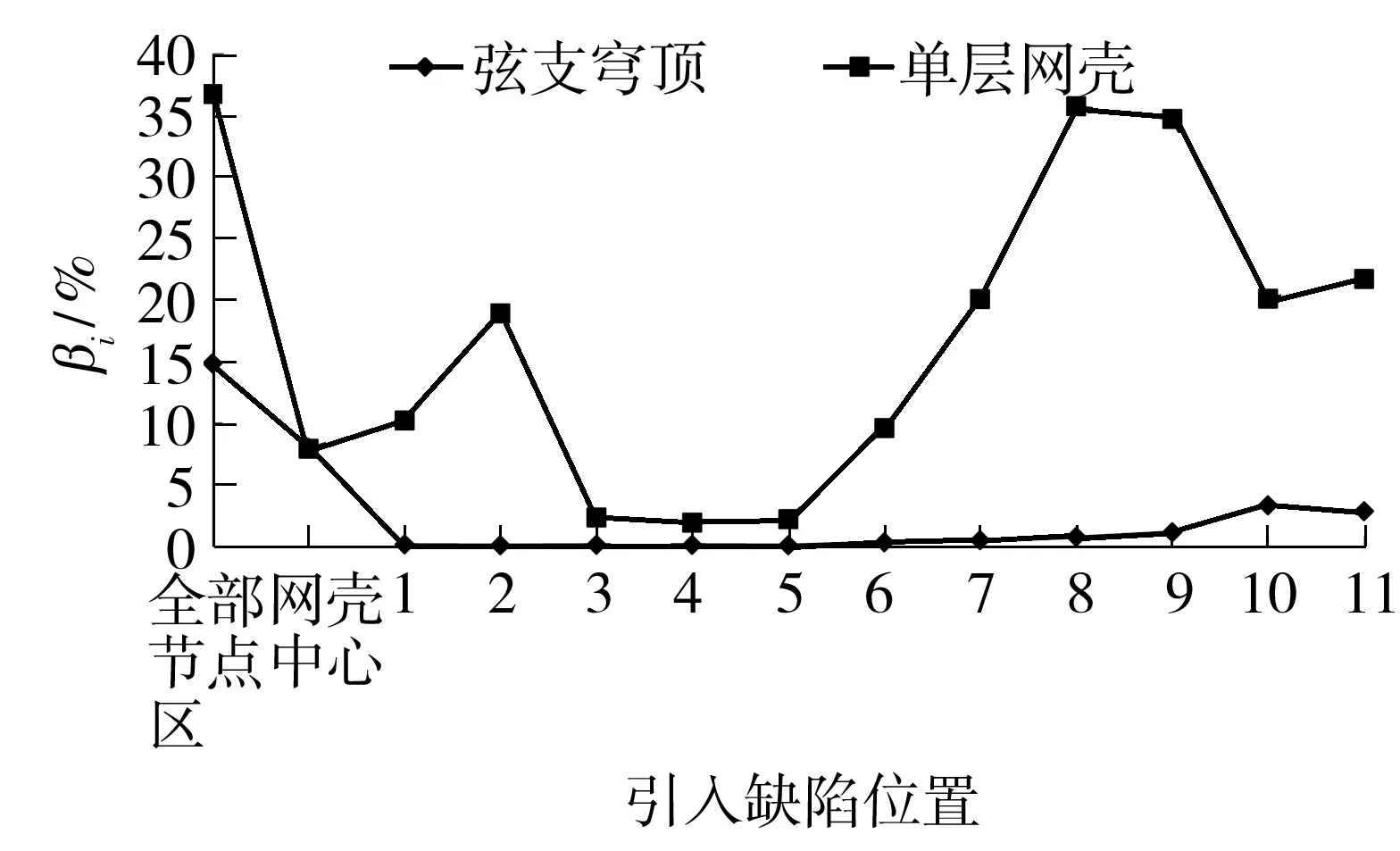
图4 弦支穹顶和相应单层网壳的βi值对比
Fig.4 Comparison ofβibetween suspended dome and corresponding-single layer reticulated shell
3.4 局部拓扑形式改变的影响
由于建筑造型的需要,该结构上部单层网壳中心区域采用花瓣状网格(见图1(d)),与传统的凯威特-联方型单层网壳相比,此区域杆件布置发生较大变化.为探讨局部拓扑形式改变对结构缺陷敏感区域的影响,在此对上部单层网壳网格形式为传统凯威特-联方型,而其他条件与图1保持不变的弦支穹顶结构进行分析.为方便对比,将图1的分析模型称为弦支穹顶1,上部单层网壳如图5所示的分析模型称为弦支穹顶2.
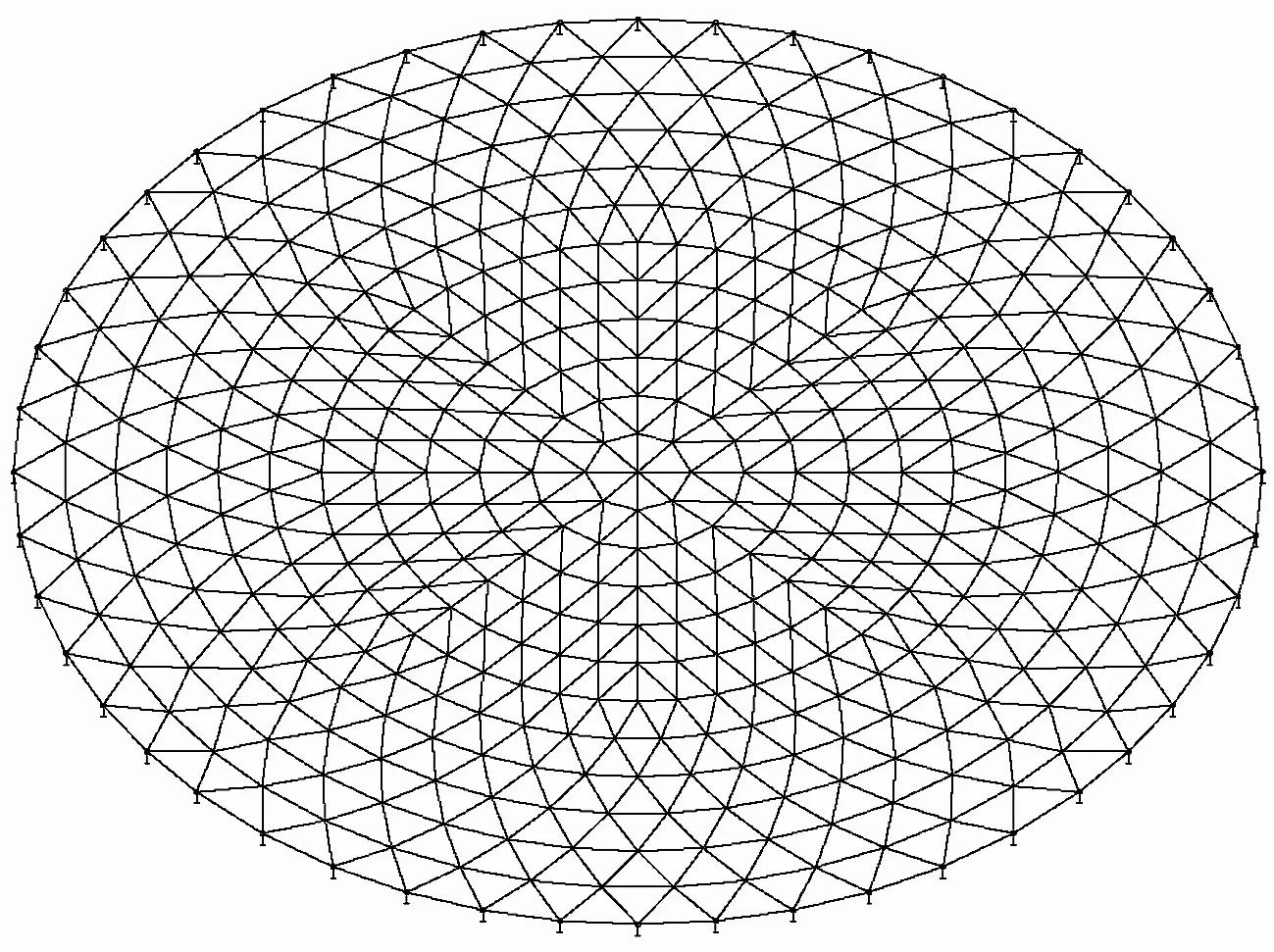
图5 传统拓扑形式的上部单层网壳
Fig.5 Upper single-layer reticulated shell with traditional topological form
组合1作用下,弦支穹顶2上部单层网壳缺陷敏感区域的分析结果见表6.由表6中可见,弦支穹顶2的缺陷敏感区域主要位于第9-11圈环杆之间.此外,βi值的变化有一个明显的递增过程.
表6 弦支穹顶2上部单层网壳的缺陷敏感区域1)
Table 6 Imperfection sensitive region of upper single layer reticulated shell for suspended dome 2
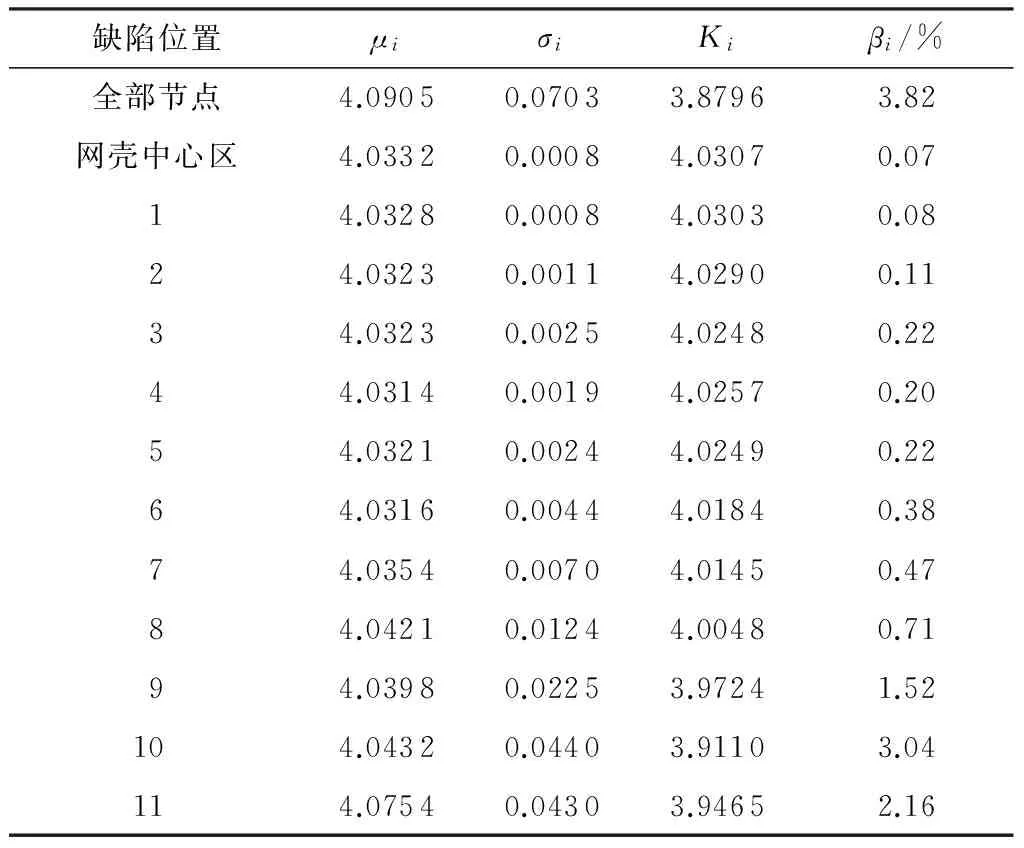
缺陷位置μiσiKiβi/%全部节点4.09050.07033.87963.82网壳中心区4.03320.00084.03070.0714.03280.00084.03030.0824.03230.00114.02900.1134.03230.00254.02480.2244.03140.00194.02570.2054.03210.00244.02490.2264.03160.00444.01840.3874.03540.00704.01450.4784.04210.01244.00480.7194.03980.02253.97241.52104.04320.04403.91103.04114.07540.04303.94652.16
1)组合1作用下无缺陷结构的稳定承载力系数K=4.034.
组合1作用下两个分析模型的βi值对比见图6.图中可见,对于弦支穹顶2,其上部单层网壳中心区域并不属于缺陷敏感区域.此外,两个模型其他区域的βi值相当接近.由此表明,改变结构局部的拓扑形式,即将该结构上部单层网壳中心区域原特殊造型的花瓣状网格改为传统的凯威特型网格布置,可有效降低结构的缺陷敏感程度.
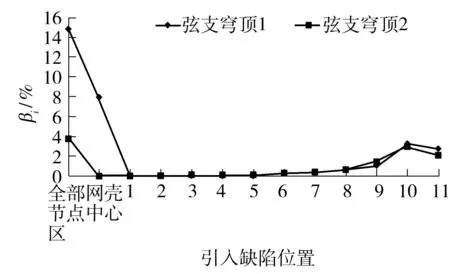
图6 两个模型的βi值对比Fig.6 Comparison of βi between two models
3.5 活载半跨分布的影响
在组合1分析的基础上,进一步探讨活载半跨分布对弦支穹顶结构缺陷敏感区域的影响.图7、8分别为不同组合作用下弦支穹顶1、2的βi值对比.
由图7可见,不同组合作用下弦支穹顶1的βi值变化趋势相近,尤其是在第3-11圈环杆区域,其变化曲线几乎重合.不同的是,组合1作用下,仅网壳中心区域属于缺陷敏感区域,组合3作用下,范围扩大至第1圈环杆节点,而组合2作用下,其范围进一步扩大至第2圈环杆节点.

图7 不同组合作用下弦支穹顶1的βi值对比
Fig.7 Comparison ofβifor suspended dome No.1 under diffe-rent load combinations

图8 不同组合作用下弦支穹顶2的βi值对比
Fig.8 Comparison ofβifor suspended dome 2 under different load combinations
由图8可见,不同组合作用下,弦支穹顶2的第9-11圈环杆之间区域均为缺陷敏感区域.此外,组合2作用下,第8圈环杆节点对缺陷敏感程度较高;组合3作用下,上部单层网壳中心区同样也属于缺陷敏感区域.结合图7、8可以发现,活载的半跨分布对传统拓扑形式弦支穹顶结构缺陷敏感区域的影响并不大,但对于本工程花瓣状网格布置单层网壳中心区域的影响较为显著.
4 结论
文中通过对大跨度椭圆抛物面弦支穹顶结构的缺陷敏感区域分析,得出以下结论:
(1)文中结构的缺陷敏感区域位于上部单层网壳,而下部索杆体系对缺陷的敏感程度很低.工程实践中,对类似结构进行非线性屈曲分析时,为减少计算工作量,建议仅在上部单层网壳中引入初始几何缺陷,即可满足工程精度要求.
(2)弦支穹顶与相应单层网壳的缺陷敏感区域有较大差异,且其影响范围和敏感程度均小于相应的单层网壳,下部索杆体系的引入明显改善了上部单层网壳的缺陷敏感性.
(3)改变结构局部的拓扑形式,即将该结构上部单层网壳中心区域原特殊造型的花瓣状网格改为传统的凯威特型网格布置,可有效降低结构的缺陷敏感程度.
(4)活载全跨分布下,该结构上部单层网壳中心区域对缺陷敏感程度最高,而支座附近区域对缺陷敏感程度次之;活载的半跨分布对传统拓扑形式弦支穹顶结构缺陷敏感区域的影响并不大,但对于本工程花瓣状网格布置单层网壳中心区域的影响较为显著.
[1] MAMORU K,MASARU A,TATSUO H,et al.On a structural system “suspen-dome” system [C]∥Proceedings of IASS Symposium.Istanbul:[s.n.],1993:523- 530.
[2] MAMORU K,MASARU A,TATSUO H,et al.Structural tests on the “suspen-dome” system [C]∥Proceedings of IASS Symposium.Atlanta:[s.n.],1994:383- 392.
[3] 张爱林,张晓峰,葛家琪,等.2008奥运羽毛球馆张弦网壳结构整体稳定分析中初始缺陷的影响研究 [J].空间结构,2006,12(4):8- 12. ZHANG Ai-lin,ZHANG Xiao-feng,GE Jia-qi,et al.Influence of initial geometrical imperfections on stability of a suspendome for badminton arena for 2008 Olympic Games [J].Spatial Structures,2006,12(4):8- 12.
[4] 刘学春,张爱林,葛家琪,等.施工偏差随机分布对弦支穹顶结构整体稳定性影响的研究 [J].建筑结构学报,2007,28(6):76- 82. LIU Xue-chun,ZHANG Ai-lin,GE Jia-qi,et al.Study on the influence of construction deviation random distribution on the integral stability of suspend-dome [J].Journal of Building Structures,2007,28(6):76- 82.
[5] 杜文风,喻福东.沁阳市体育馆椭圆抛物面弦支穹顶稳定性研究 [J].建筑结构,2013,43(22):39- 42,38. DU Wen-feng,YU Fu-dong.Stability research on elliptic paraboloid shaped suspend-dome structural system of Qinyang Municipal Gymnasium [J].Building Structure,2013,43(22):39- 42,38.
[6] 赵均,徐金蓓,甘明,等.椭球面弦支穹顶结构的稳定性 [J].北京工业大学学报,2013,39(12):1821- 1826. ZHAO Jun,XU Jin-bei,GAN Ming,et al.Stability analysis of ellipsoid suspend-dome [J].Journal of Beijing University of Technology,2013,39(12):1821- 1826.
[7] 唐敢.板片空间结构缺陷稳定分析及试验研究 [D].南京:东南大学土木工程学院,2005.
[8] 唐敢,赵惠麟,郭小明.板片空间结构缺陷敏感区域 [J].东南大学学报(自然科学版),2006,36(6):1002- 1006. TANG Gan,ZHAO Hui-lin,GUO Xiao-ming.Imperfection sensitive region in sheet-space structure [J].Journal of Southeast University(Natural Science Edition),2006,36(6):1002- 1006.
[9] 刘红亮.大跨度弦支穹顶结构的缺陷敏感区域及动力稳定性研究[D].广州:华南理工大学土木交通学院,2015.
[10] 蔡健,贺盛,姜正荣,等.单层网壳结构稳定分析中初始几何缺陷最大值的研究 [J].建筑结构学报,2015,36(6):86- 92. CAI Jian,HE Sheng,JIANG Zheng-rong,et al.Investigation on maximum value of initial geometric imperfection in stability analysis of single layer reticulated shells [J].Journal of Building Structures,2015,36(6):86- 92.[11] 姜正荣,王仕统,石开荣,等.厚街体育馆大跨度椭圆抛物面弦支穹顶结构的非线性屈曲分析 [J].土木工程学报,2013,46(9):21- 28. JIANG Zheng-rong,WANG Shi-tong,SHI Kai-rong,et al.Nonlinear buckling analysis of long-span elliptic paraboloid suspended dome structure for Houjie Gymnasium [J].China Civil Engineering Journal,2013,46(9):21- 28.
[12] Gioncu V.Buckling of reticulated shells:state-of-the-art [J].International Journal of Space Structures,1995,10(1):1- 46.
[13] 宋天霞,邹时智,杨文兵.非线性结构有限元计算 [M].武汉:华中理工大学出版社,1996.
[14] 郭佳民,董石麟,袁行飞.随机缺陷模态法在弦支穹顶稳定性计算中的应用 [J].工程力学,2011,28(11):178- 183. GUO Jia-min,DONG Shi-lin,YUAN Xing-fei.Application of random imperfection mode method in stability calculation of suspen-dome [J].Engineering Mechanics,2011,28(11):178- 183.
Analysis of Imperfection Sensitive Region of Long-Span Elliptic Paraboloid Suspended Dome Structure
JIANGZheng-rong1,2SHIKai-rong1,2LIUHong-liang1CAIJian1,2LUOBin3
(1.School of Civil Engineering and Transportation, South China University of Technology, Guangzhou 510640, Guangdong, China;2.State Key Laboratory of Subtropical Building Science, South China University of Technology, Guangzhou 510640, Guangdong,China;3.School of Civil Engineering, Southeast University, Nanjing 210096, Jiangsu, China)
A long-span elliptic paraboloid suspended dome structure, in which the clear span between supports is 110 m×80 m and the rise of the upper single-layer reticulated shell is 9.4 m, is employed in the steel roof of Houjie Gymnasium. The imperfection sensitive regions of the structure and the corresponding single-layer reticulated shell are comparatively investigated by means of the advanced random imperfection mode method. On this basis, the influences of the local topological form change and the half-span distribution of the live loads on the imperfection sensitive region of the suspended dome are further discussed. The results show that (1) the imperfection sensitive region of the suspended dome is located in the upper single-layer reticulated shell; (2) the imperfection sensitive region of the suspended dome is significantly different from that of the corresponding single-layer reticulated shell, and owing to the introduction of the lower cable-strut system, the imperfection sensitivity of the upper single-layer reticulated shell is remarkably improved; (3) by changing the local topological form, the imperfection sensitivity of the structure can be effectively reduced; and (4) the half-span distribution of the live loads has little influence on the imperfection sensitive region of the suspended dome with a traditional topological form, but has a significant influence on the central region of the upper single-layer reticulated shell of this kind of suspended dome.
suspended dome; single-layer reticulated shell;stability random imperfection mode method; imperfection sensitive region
2016- 02- 26
国家“十二五”科技支撑计划项目(2012BAJ03B06);广州市科技计划项目(1563000257) Foundation item: Supported by the National Key Technology Research and Development Program of the Ministry of Science and Technology of China during the“12th Five-year Plan”(2012BAJ03B06)
姜正荣(1971-),男,博士,副教授,主要从事钢结构、大跨度空间结构研究.E-mail:zhrjiang@scut.edu.cn
† 通信作者: 石开荣(1978-),男,博士,副教授,主要从事预应力钢结构、大跨度空间结构研究.E-mail:krshi@scut.edu.cn
1000- 565X(2016)12- 0112- 08
TU 393.3
10.3969/j.issn.1000-565X.2016.12.016
