自动对中式汽车回转台动态特性及仿真*
2016-02-14吴上生林旺阳戴水文
吴上生 林旺阳 戴水文
(1.华南理工大学 机械与汽车工程学院, 广东 广州 510640; 2.广东明和智能设备有限公司, 广东 广州 511455)
自动对中式汽车回转台动态特性及仿真*
吴上生1林旺阳1戴水文2
(1.华南理工大学 机械与汽车工程学院, 广东 广州 510640; 2.广东明和智能设备有限公司, 广东 广州 511455)
提出了一种平面移动式立体车库用的自动对中式汽车回转台,分析了其自动对中的工作原理和液压系统回路;建立了对称阀控非对称液压缸动力机构的模型,推导了液压缸活塞杆位移和伺服阀阀芯位移的传递函数;在AMESim和Simulink中分别建立了液压系统模型和输入信号模型,推导了输入信号和活塞杆位移的开环传递函数,论证了此闭环系统的稳定性;应用AMESim/Simulink对液压系统回路的动态特性进行联合仿真,得到了不同输入条件下两活塞杆位移曲线以及两活塞杆位移的误差曲线.仿真结果表明,两活塞杆位移存在一定失真度但属于正常现象,说明该装置可行并有效.
自动对中;液压系统回路;液压缸;伺服阀;联合仿真
汽车回转台是平面移动式立体车库中重要的设备之一,具有能在狭小空间内自动转向的优点[1].传统的汽车回转台通过采用外置式来提高进车时车辆的对中度,这样的设计增加了司机的停车难度,同时需要与搬运器结合才能将车辆送入提升井中,并且需要占用额外的面积而减小停车密度.液压系统具有高精度、高响应等显著优点[2],作为液压系统的执行元件,液压缸质量轻、惯性小、集成度高且力矩大,方便过载保护设计[3- 4],同时非对称液压缸具有结构紧凑、工作可靠及生产成本低等优点,因而广泛应用于车辆、工程机械、矿山机械等的液压系统中[5].
文中应用液压缸驱动技术解决汽车回转台自动对中的运动特性问题,提出一种用于平面移动式立体车库的自动对中式汽车回转台,汽车回转台内置于立体车库的提升井中,采用液压缸驱动方式实现车辆在载车板上的自动对中.应用AMESim软件建立相应的液压系统同步缸位置同步回路模型,利用Simulink建立仿真控制模块,对位置同步回路控制的稳定性进行验证,对液压缸活塞杆的位移输出进行Matlab/Simulink联合仿真,得到其活塞杆位置同步的失真度,据此验证该液压缸驱动自动对中装置的可行性以及有效性.
1 自动对中式汽车回转台工作原理
根据平面移动式立体车库的整体结构,基于液压传动系统的原理设计了如图1所示的自动对中式汽车回转台,其运动状态主要包括旋转盘的旋转运动、提升臂的上下运动和液压缸活塞杆的水平运动.存车时,旋转盘5旋转90°,待存车辆开进到梳齿型载车板4上后,旋转盘5往回旋转90°而回到原位置,梳齿型载车板4下方的提升臂1开始上升直到刚好提起待存车辆,此时待存车辆离开梳齿型载车板4交换至提升臂1的导轮梳齿架上,液压缸3伸出活塞杆开始进行对中过程,完成对中后活塞杆回到液压缸内,待存车辆的中心线与梳齿架中心线吻合.
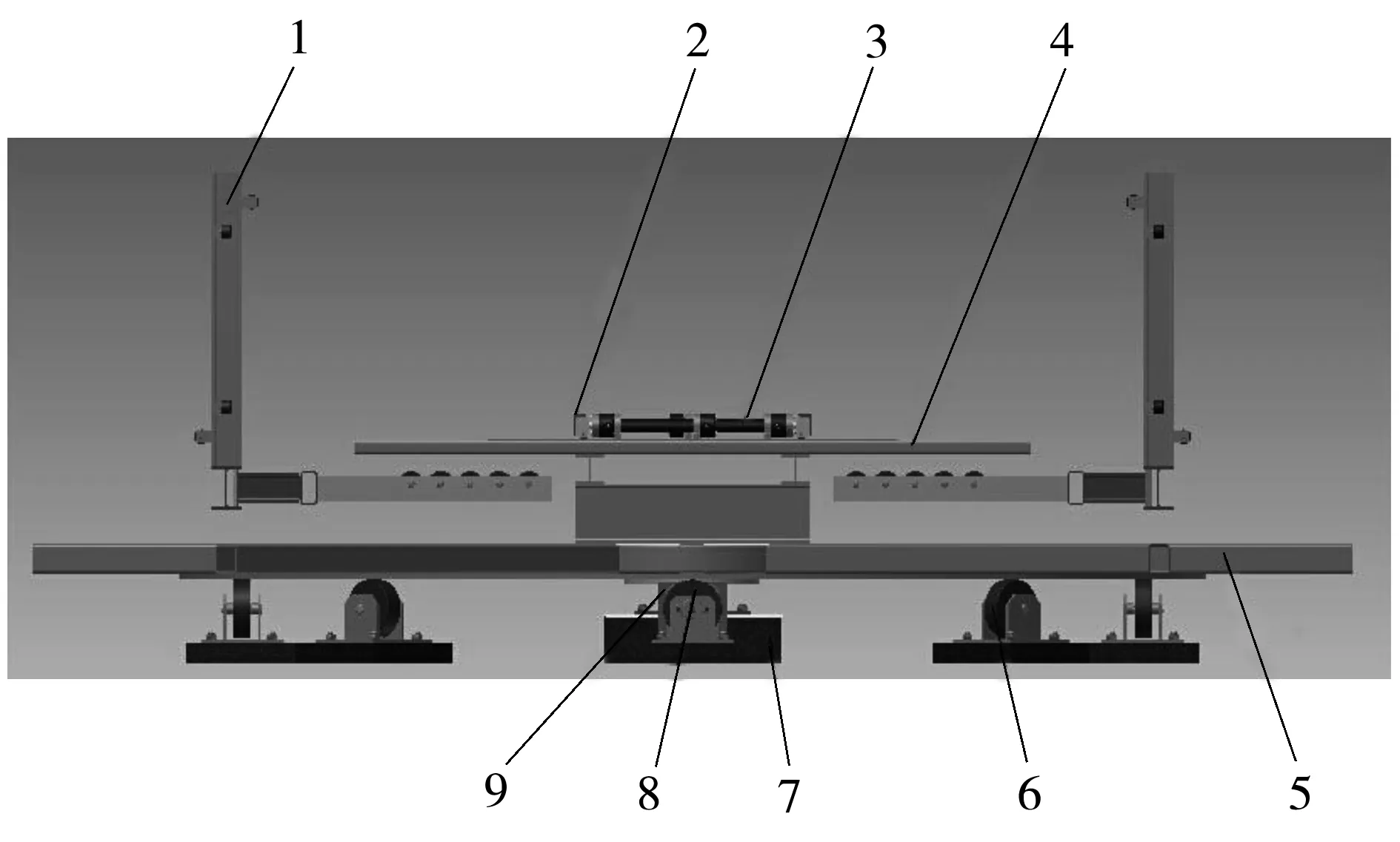
图1 自动对中式汽车回转台结构Fig.1 Structure of automatic centering car rotary platform
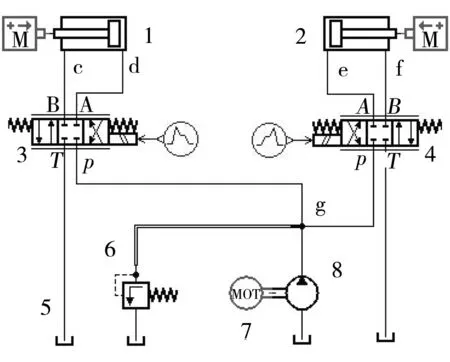
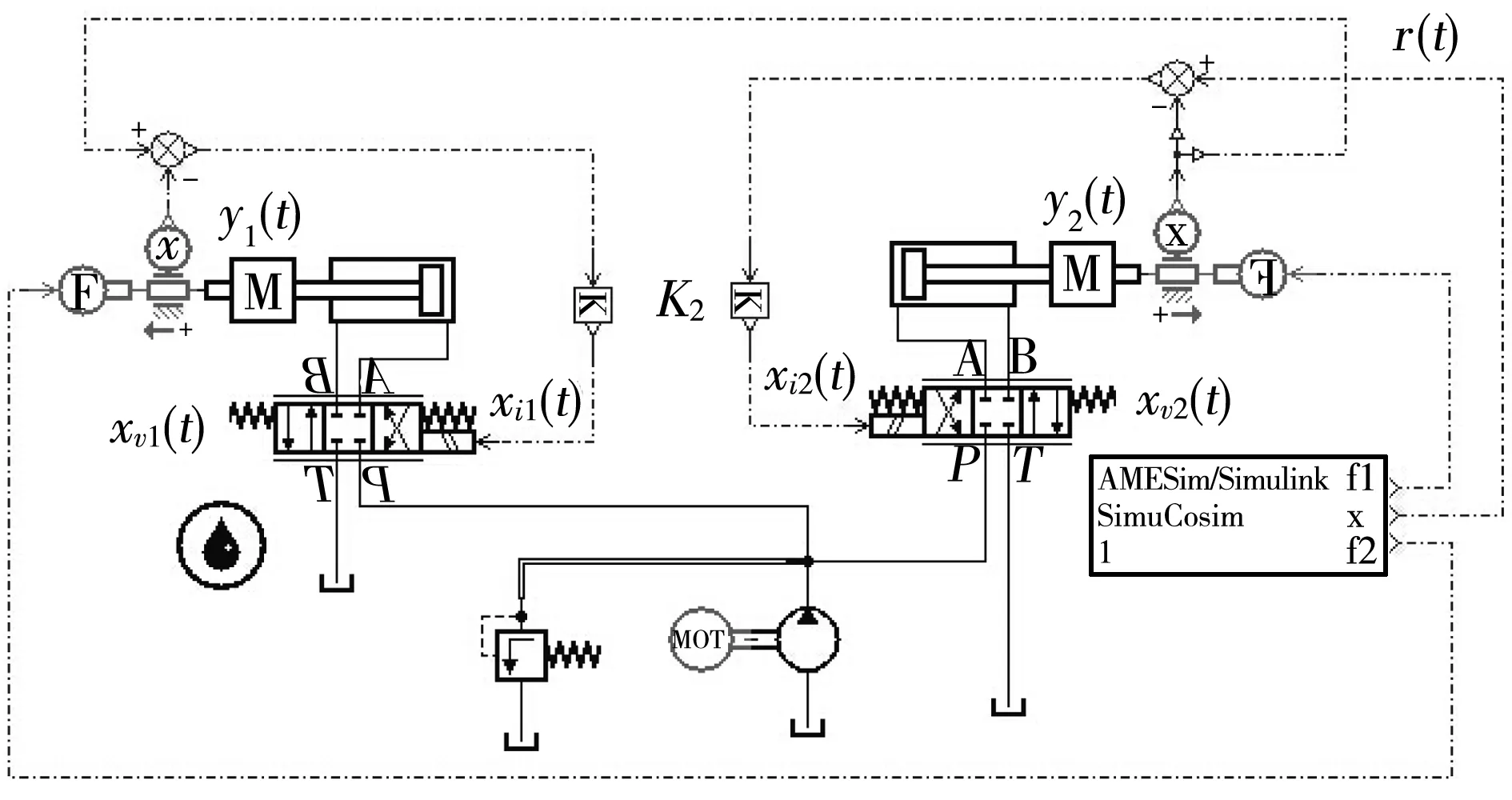
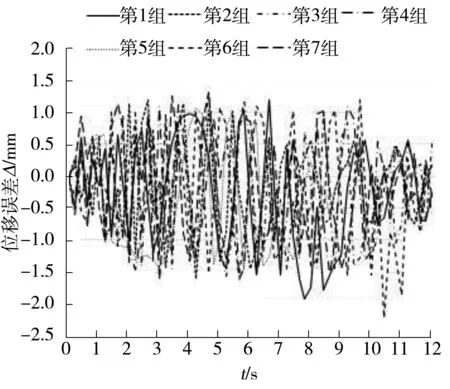
对中过程如图2所示,假定待存车辆车轮相对角铁的初始位置如图2(a)所示,左间距为x1,右间距为x2,且x1 图2 对中过程示意图Fig.2 Schematic diagram of automatic centering process 2.1 液压缸位置同步回路设计 根据自动对中的原理,设计了如图3所示的液压缸位置同步回路,使系统中两个活塞杆在理论上实现运动的同步[6- 7]. 如图3所示,在液压系统同步回路中,主要包括两台液压缸、两台电磁换向阀、油箱、溢流阀、液压泵和电机等,液压缸采用的是非对称液压缸即单活塞杆液压缸,电磁换向阀采用的是对称的三位四通伺服阀.通过两台对称阀3、4分别控制两台非对称液压缸1、2的运动状态,采用完全相同的液压缸、伺服阀以及管道,在理想情况且外力条件相同时,两活塞杆的位移轨迹相吻合,则实现位置的同步控制. 图3 液压缸位置同步回路Fig.3 Position synchronous circuit of hydraulic cylider 2.2 对称阀控非对称液压缸动力机构分析 根据图3所示的液压系统回路中的液压缸和伺服阀,可得到如图4所示的对称阀控非对称液压缸动力机构模型.非对称液压缸的两腔面积不等,典型的非对称液压缸有单活塞杆液压缸[8- 9]. 图4 对称阀控非对称液压缸动力机构 Fig.4 Power mechanism of asymmetric hydraulic cylider controlled by symmetric valve 无杆腔(即进液腔)的流量连续方程为 (1) 式中:Q1为液压缸进液管路流量,m3/s;Ci、Ce为液压缸内、外泄漏系数,m3/(s·Pa);p1、p2为液压缸无杆腔、有杆腔压力,Pa;A1为液压缸无杆腔面积,m2;y为活塞杆位移,m;V1为液压缸进液腔液体容积,m3;βe为液体体积弹性模量,Pa. 王传礼等[10]总结前人的研究得出以下结论,以定义QL和pL: (2) 式中,A2为液压缸有杆腔面积. 根据流体力学,理想状态下的阀流量方程为 (3) (4) 式中:cd为伺服阀阀口流量系数;w为伺服阀节流口面积梯度,m;xv为伺服阀阀芯位移,m;ρ为油源密度,kg/m3;pS为油源压力,Pa. 结合式(1)-(4)得到 (5) (6) 式中:Vt1为等效总容积,m3,Vt1=4V1/(1+n3);Ctp1为等效泄漏系数,m3/(s·Pa);Cts1为附加泄漏系数,m3/(s·Pa). 由式(3)、(5)得到伺服阀负载流量方程: (7) 则线性化方程 QL=kqxv-kcpL (8) 液压缸的力平衡方程为 (9) 式中:B为粘性阻尼系数,N·s/m;K为弹性刚度,N/m;FL为负载力,N;m为活塞杆的等效质量,kg. 对式(6)、(8)-(9)进行拉式变换,得 (10) QL=kqXv-kcpL (11) A1pL=(ms2+Bs+K)Y+FL (12) 由式(10)-(12)得到阀控液压缸动力机构的关系式[11- 12]: 式中,Kce1为总流量压力系数,Kce1=Kc+Ctp1. 文中所述的液压系统中无弹性负载,即K=0,且存在BKce1≪1,mKce1≪1,A1Cts1PS≪1,所以将上式近似简化为 (13) 2.3 系统参数及传递函数确定 根据液压系统的实际情况,得到系统的参数如下:cd=0.62,w=0.01 m,ρ=870 kg/m3,βe=1.4×109Pa,Ce=0 m3/(s·Pa),Ci=5×10-11m3/(s·Pa),pS=9×106Pa,pL=6×106Pa,B=500 N·s/m,m=26.843 kg,FL=4×103N,K=0 N/m,A1=1.26×10-3m2,A2=0.88×10-3m2,Ctp1=5.55×10-11m3/(s·Pa),kq=0.444,Ctp2=3.88×10-11m3/(s·Pa),Vt1=0.9×10-3m3.PL为工作压力,Pa. 将上述数据代入式(13),得到活塞杆位移与伺服阀阀芯位移的关系式: 对上面等式右边第(2)式进行反拉式变换,得到 0.14coswnt-0.24sinwnt. 其中,频率wn=606Hz,周期T=0.00165s,在仿真采样时间设定为0.01s的条件下,将此干扰在计算中忽略.故在后续计算中假定传递函数 (14) 3.1 液压系统AMESim仿真模型的建立 根据图3所示的液压系统位置同步回路,为克服负载、摩擦阻力、泄漏、制造质量和结构变形的差异,增加了合适的控制模块和负反馈控制,使系统在不同负载下实现高精度的位置同步运动,并在AMESim平台中绘出仿真模型,如图5所示[13- 14]. 给定位移目标信号r(t),即输入位移信号;y1(t)和y2(t)为位置传感器检测信号,即输出位移信号.活塞直径为40mm,活塞杆直径为22mm,活塞杆最大行程为0.3 m,m=28.843 kg;库仑摩擦力为100 N,静摩擦力为100 N,内泄漏系数为10-7L/(min·Pa),其他采用系统的默认参数[15- 16]. 图5 同步回路AMESim仿真模型Fig.5 Simulation model of synchronous circuit in AMESim 3.2 系统传递函数的建立 若存在负载时系统稳定,则空载时稳定,故只分析式(13)中代入具体负载值FL=4×103N时的系统稳定性,且负载值安全系数约为2.根据图5的液压传动系统,得到输入与输出的传递函数方框图,如图6所示. 图6 系统传递函数方框图Fig.6 Block diagram of system transfer function 根据图6的方框图,得到液压传动系统输出与输入信号的开环传递函数为 GK(s)=K2G1(s)GF(s) (15) 其中增益 K2=1 000 (16) G1(s)为伺服阀阀芯位移与输入电信号之间的传递函数,其动态特性由一个二阶振荡环节来表示[17]: 设置AMESim液压传动系统模型中伺服阀模块的各参数为:额定电流I=10 mA,固有频率wn=100 Hz,阻尼比ξ=0.7;得伺服阀输入电流信号与阀芯位移的传递函数为 (17) 由式(14)-(17)得到系统的开环传递函数: GK(s)= (18) 3.3 系统的稳定性分析 (1)稳态误差分析 因输入信号为分段斜坡函数,根据自动控制原理的定理,单位斜坡信号的稳态误差为 在本系统中,由于输入信号的最大值Max<0.3m,且0.3ess=0.003m=3mm,对中结果的要求在10mm以内,对于传动系统来说,此稳定误差是可接受的,又因负载值的安全系数为2,故可认为实际情况下的稳态误差值小于0.01,满足误差要求. (2)动态稳定性分析 根据系统的开环传递函数GK(s),在Matlab中输入命令nyquist(num,den)得到图7所示的开环系统幅相频率特性曲线. 图7 系统的开环幅相频率特性曲线Fig.7 Open-loop amplitude phase frequency characteristic curve of system 由图7易看出,穿越点在-0.75附近,而且相角裕度γ=13°>0,幅值裕度hg=1.3>0;根据nyquist稳定判据,开环系统的幅相特性曲线在实轴(-∞~-1)区段没有穿越,即N=0;而开环系统在右半s平面也没有极点,即P=0,则N=-P=0,故闭环系统是稳定的[18].同时得到系统的幅值裕度g=1.33,相角裕度p=31.09,系统还具有一定的相对稳定性,虽然幅值裕度未到达工程一般要求的g>2(即6dB),但系统已实现稳态误差的达标,故忽略此不足之处. 对于可能减小或消除稳态误差的PI或PID控制进行检验,发现会导致系统的不稳定,结合稳态误差值以及幅相频率曲线,故采用比例控制而非PI或PID控制. 4.1 位移目标信号在Simulink中的实现 在Simulink中得到目标位移和两活塞杆负载3个输入信号,如图8所示,S-Function左端的3个接口f2、x、f1与AMESim中一一对应. 模型中的参数a=min(x1,x2),b=(x1+x2)/2,仿真时在Matlab中输入多组a、b值,从而模拟多种状态下的系统运行结果. 图8 控制系统输入信号Simulink模型Fig.8 Model of control system input signal in Smulink 4.2 负载力在Simulink中的模拟 根据图2,两活塞杆端所受的负载力的时刻是不同的,初始负载力均为0.两活塞杆同时伸出运动时,靠车轮较近的活塞杆端先受到逐渐增大的负载力,达到最大后趋于稳定值;一定时间后,另一活塞杆端才受到同样逐渐增大的负载力,达到最大值后,两活塞杆同时缩回运动,两活塞杆端的负载力同步逐渐减小至0,直到两活塞杆回到液压缸内. 故负载力由分段时间函数表示,其节点时刻随a、b变化,图8中得到目标信号的同时还得到两个跟随目标信号变化的负载力信号,其表达式如下: (19) (20) 4.3 系统基于AMESim/Simulink的联合仿真 对于普通轿车型来说,其左右轮距范围一般为1 450~1 550 mm,轮胎宽度230 mm左右,从而得到左右轮内距范围为1 220~1 320 mm,系统结构中初始状态时两液压杆间距为820 mm,得到图中b=(x1+x2)/2值的取值范围为200~250 mm,故得到表1输入参数表. 将表1中的7组数值输入到Matlab中分别运行,得到7组目标位移x输入信号曲线以及7组负载力f1、f2信号曲线,运行联合仿真,Simulink中生成的3个信号x、f1、f2输入至AMESim中,仿真结束后得到7组活塞杆1、2位移曲线和两活塞杆位移误差曲线,如图9-11所示. 表1 初始状态间距及a、b值 Table 1 Space in initial state as well asaandbvalues mm 组数x1x2ab=(x1+x2)/2150350502100300100315025015045045050510040010061503501507200300200200250 从图9和10易看出,7组数值下活塞杆的位移曲线与目标曲线几乎重合;从误差曲线图11看出,7组条件下两活塞杆位移的误差最大值为2.25 mm左右,对于活塞杆运动距离至少为0.2 m的系统来说,最大误差em=2.25/200=0.01125=1.125%,考虑到推导过程中简化及忽略了一些计算,同时将负载信号近似为阶跃信号而带来偏差,故此误差值属于正常现象,至此验证了自动对中装置的可行性. 图9 b=0.2 m时的3组位移结果曲线Fig.9 Three groups of displacement result curves when b=0.2 m 图10 b=0.25 m时的4组位移结果曲线Fig.10 Four groups of displacement result curves when b=0.25 m 图11 7组活塞杆1、2位移误差曲线 Fig.11 7 groups of displacement error curves between piston rod 1 and 2 文中提出了一种用于平面移动式立体车库的自动对中式汽车回转台,说明了其自动对中的工作原理以及实现自动对中的液压系统回路;通过分析同步回路中对称阀控非对称液压缸动力机构的模型,得到液压缸活塞杆位移和伺服阀阀芯位移之间传递函数;运用AMESim建立液压系统回路的模型,计算得到系统的开环传递函数,误差近似为0,论证了闭环系统的稳定性;运用Simulink建立仿真控制模型,通过AMESim/Simulink对系统进行联合仿真,得到了两活塞杆位移曲线及两活塞杆位移误差曲线;结果表明两活塞杆位移存在一定的失真度,但误差大小在允许范围之内,故论证了自动对中装置的可行性及有效性. [1] 程琪,许宏峰,李文杰,等.回转盘升降立体车库:200810062505.5 [P].2008- 06- 19. [2] MURRENHOFF H.Development trend of hydrau1ic con-trol technology [J].Journal of Engineering Design,1997(3):20- 29. [3] 牛玉艳.基于Ansys的液压缸有限元分析 [D].成都: 西南交通大学机械工程学院,2012. [4] 刘晓明,叶玮.液压缸结构设计及运行特性分析 [J].液压气动与密封,2013,33(7):17- 21. LIU Xiao-ming,YE Wei.Structure design and analysis on operating property of hydraulic cylinder [J].Hydraulics Pneumatics and Seals,2013,33(7):17- 21. [5] 郝前华,何清华,贺继林,等.非对称液压缸的动态特性仿真研究 [J].广西大学学报(自然科学版),2010,35(6):984- 988. HAO Qian-hua,HE Qing-hua,HE Ji-lin,et al.Simulation study on dynamic characteristics of asymmetrical hydraulic cylinder [J].Journal of Guangxi University(Natural Science Edition),2010,35(6):984- 988. [6] 邓飙,苏文斌,郭秦阳,等.双缸电液位置伺服同步控制系统的智能控制 [J].西安交通大学学报,2013,45(11):85- 90. DENG Biao,SU Wen-bin,GUO Qin-yang,et al.Intelligent control for electro-hydraulic position servo Synchronic control system with double cylinders [J].Journal of Xi’an Jiangtong University,2013,45(11):85- 90. [7] 姜继海,宋锦春,高常识.液压与气压传动 [M].北京:高等教育出版社,2002. [8] 许贤良,王传礼.液压传动系统 [M].北京:国防工业出版社,2008. [9] 王林鸿,吴波,杜润生,等.液压缸运动的非线性动态特征 [J].机械工程学报,2007,43(12):12- 19. WANG Lin-hong,WU Bo,DU Run-sheng,et al.Nonlinear dynamic characteristics of moving hydraulic cylinder [J].Chinese Journal of Mechanical Engineering,2007,43(12):12- 19. [10] 王传礼,许贤良.阀控非对称液压缸机构建模探讨 [J].矿山机械,1998(7):66- 68. WANG Chuan-li,XU Xian-liang.Model discussion about mechanism of asymmetric hydraulic cylinder controlled by valve [J].Mining and Processing Equipment,1998(7):66- 68. [11] 张晓宁,王岩,付永领.非对称液压缸对称性控制[J].北京航空航天大学学报,2007,33(11):1334- 1339. ZHANG Xiao-ning,WANG Yan,FU Yong-ling.Symme-tric control of asymmetric cylinder [J].Journal of Beijing University of Aeronautics and Astronautics,2007,33(11):1334- 1339. [12] 王传礼,丁凡,李其朋,等.对称四通阀控非对称液压缸伺服系统动态特性研究[J].中国机械工程,2004,15(6):471- 474. WANG Chuan-li,DING Fan,LI Qi-peng,et al.Research on dynamic characteristics of asymmetric cylinder controlled by symmetric four-way valve [J].China Mecha-nical Engineering,2004,15(6):471- 474. [13] HOGON P,BURROWS C R.Synchronizing unevenly-loaded hudraulic cylinders [J].Proceedings of the ASME Fluid Power and Systems Technology Division,1994(1):75- 80. [14] HA Q P,RYE D C,DURRANT Whyte H F.Fuzzy mo-ving sliding mode controlwith applieation to robotic Manipulators [J].Automatiea,1999,35(9):607- 616. [15] MARQUIS-FAVRE W,BIDEAUX E,SCAVARDA S.A planar mechanical library in the AMESim simulink simu-lation software,part I:formulation of dynamics [J].Simlulation Modelling Practice and Theory,2006,14(1):25- 46. [16] BIDEAUX E,SCAVARDA S.A pneumatic library for AMESim [C]∥Proceedings of ASME International Mechanical Engineering Conference and Exhibition.Anaheim:[s.n.],1998:185- 195. [17] 刘海丽,李华聪.液压机械系统建模仿真软件AMESim及其应用 [J].机床与液压,2006(6):124- 126. LIU Hai-li,LI Hua-cong.Modeling and simulation software AMESim and its application for hydraulic-mechanic system [J].Machine Tool and Hydraulics,2006(6):124- 126. [18] 高国燊,余文烋,彭康拥,等.自动控制原理 [M].广州:华南理工大学出版社,2009. Dynamic Characteristics of Automatic-Centering Rotary Platform for Cars and Its Simulation WUShang-sheng1LINWang-yang1DAIShui-wen2 (1.School of Mechanical and Automotive Engineering, South China University of Technology, Guangzhou 510640,Guangdong, China;2. Guangdong Minghe Intelligent Equipment Co.,Ltd., Guangzhou 511455, Guangdong, China) Proposed in this paper is an automatic-centering rotary platform for a kind of planar movable stereo car garage, and its automatic centering principle and hydraulic system circuit are analyzed. Then, a power mechanism model of the asymmetric hydraulic cylinder controlled by the symmetric valve is constructed, and a transfer function between the piston rod displacement of the hydraulic cylinder and the spool displacement of the servo-valve is derived. Moreover, a model of the hydraulic system and a model of the input signal are constructed respectively by using AMESim and Simulink, and an open-loop transfer function between the input signal and the piston rod displacement is deduced to verify the stability of the closed-loop system. Finally, the dynamic characteristics of the hydraulic system circuit is collaboratively simulated by using AMESim/Simulink, thus achieving the displacement curves and displacement error curves of two piston rods under different input conditions. Simulation results demonstrate that, for the displacement of the two piston rods, there exists a certain distortion, but it is a normal phenomenon, which means that the proposed platform is both feasible and effective. automatic centering; hydraulic system circuit; hydraulic cylinder; servo-valve; co-simulation 2016- 03- 22 广东省科技计划项目(2013B011301006) Foundation items: Supported by the Science and Technology Planning Project of Guangdong Province,China(2013B011301006) 吴上生(1963-),男,博士,教授,主要从事机械装备自动控制理论与应用研究.E-mail:shshwu@scut.edu.cn 1000- 565X(2016)12- 0023- 07 TH 122 10.3969/j.issn.1000-565X.2016.12.004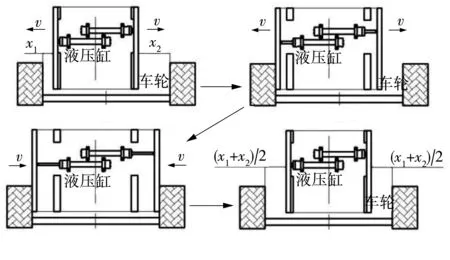
2 液压缸位置同步回路设计与分析
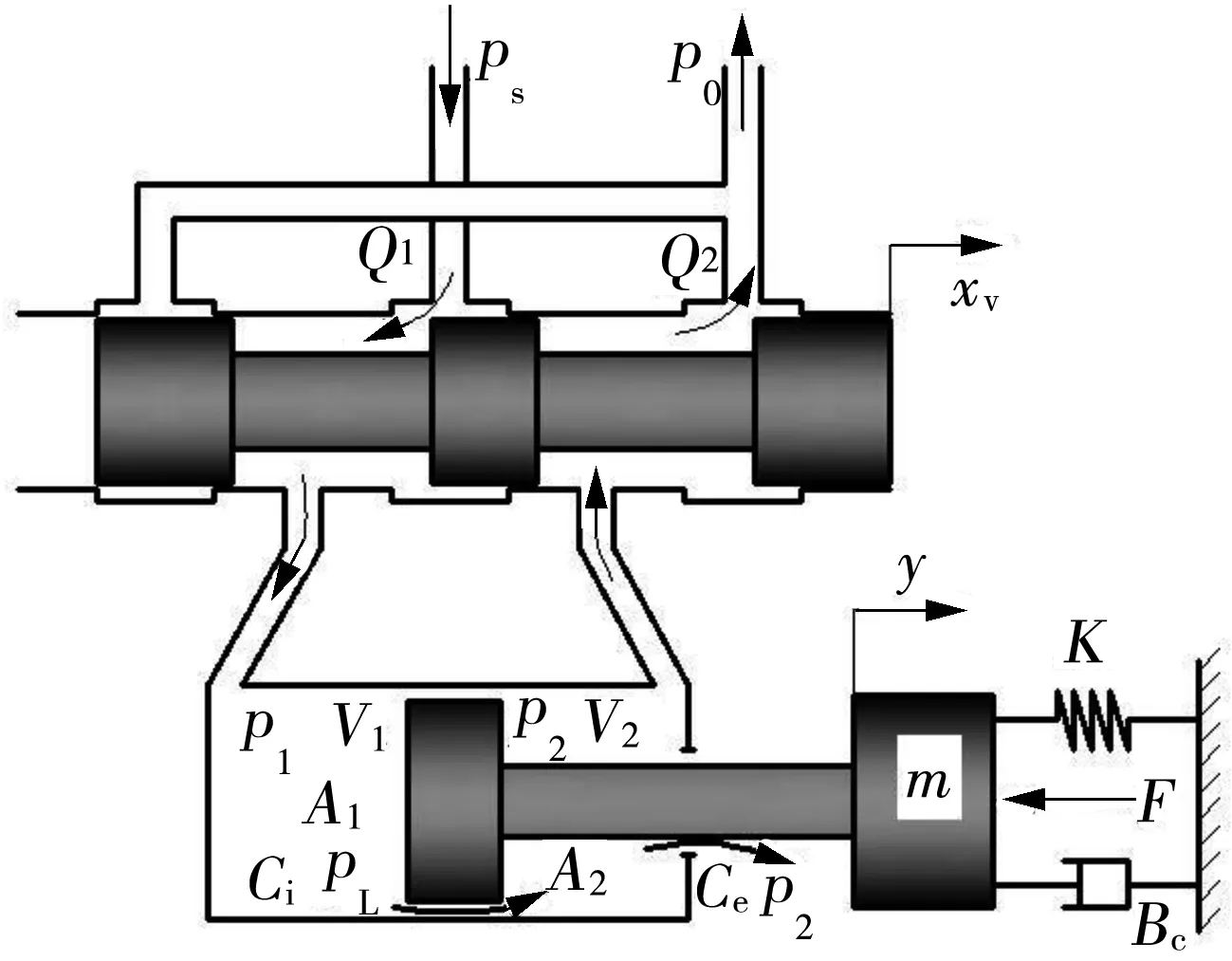
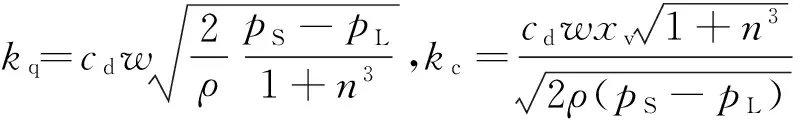

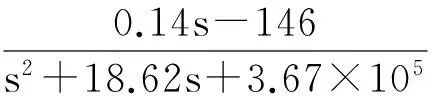
3 液压系统模型的建立以及稳定性分析


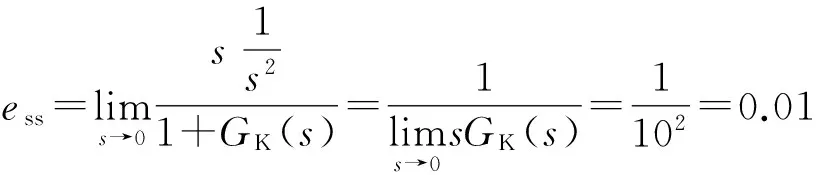
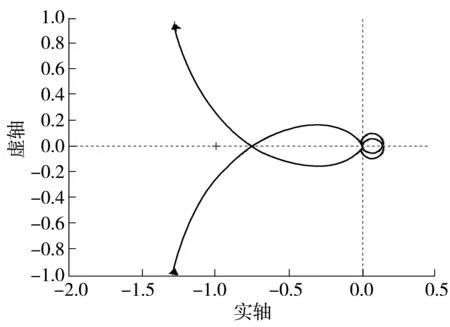
4 动态特性联合仿真
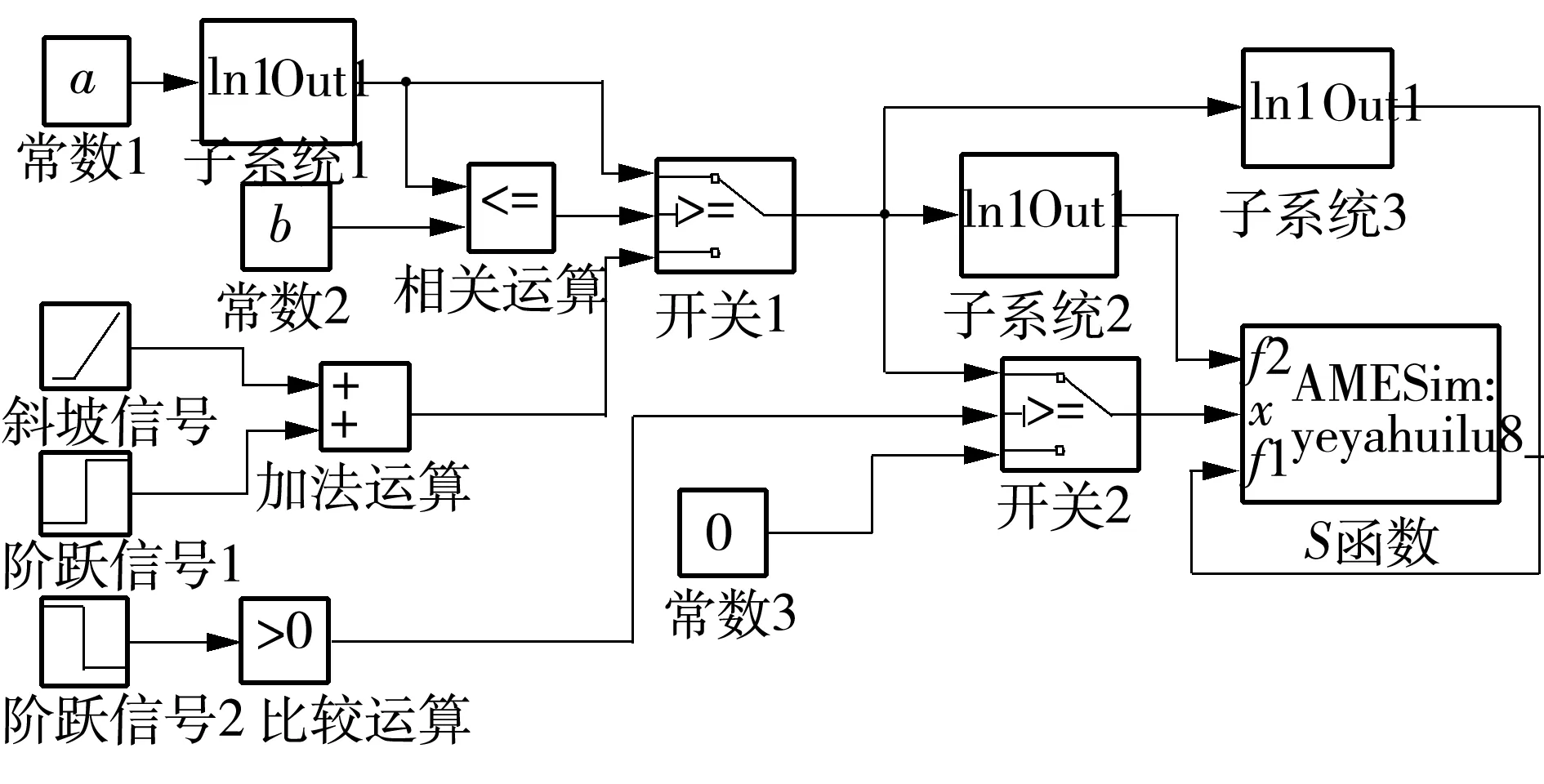

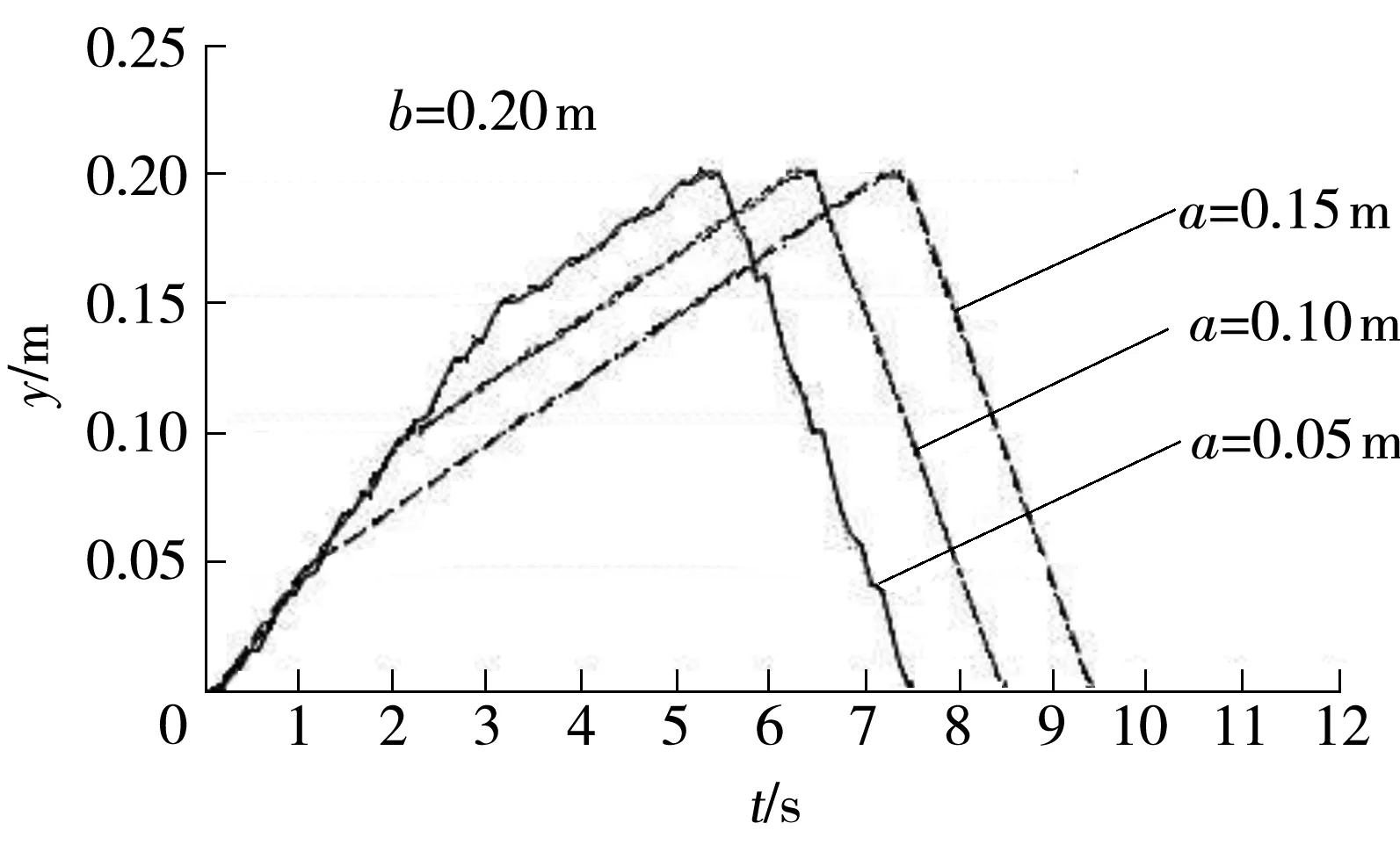
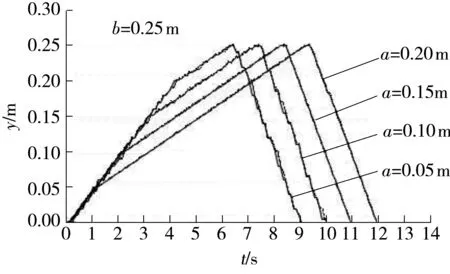
5 结论
