基于SVD的抗差UKF算法在短时交通流状态估计中的应用*

许伦辉 王祥雪

(华南理工大学 土木与交通学院， 广东 广州 510640)

基于SVD的抗差UKF算法在短时交通流状态估计中的应用*

许伦辉 王祥雪

(华南理工大学 土木与交通学院， 广东 广州 510640)

针对城市区域快速路网，以实现交通流运行状态实时估计为目标，建立宏观交通流状态空间模型，在实现交通流状态估计的同时，更新交通流模型参数，提高交通流模型的适应性和准确性.然后提出了基于奇异值分解(SVD)的优化抗差无损卡尔曼滤波(UKF)算法，用奇异值分解代替标准UKF的Cholesky分解，解决了协方差矩阵非正定时滤波计算不能持续的问题，同时，该算法根据观测协方差矩阵是否病态选择抗差因子，对增益矩阵和观测协方差矩阵进行自适应计算，进而抑制由于模型较高的非线性带来的误差.通过实验证明，文中所提算法避免了扩展卡尔曼滤波(EKF)算法的滤波发散问题，能准确跟踪交通流的变化趋势，提高交通流状态估计的稳定性和精度.

交通流状态空间模型；UKF算法；奇异值分解；抗差因子

日益严峻的交通拥堵状况为制定、优化交通诱导及控制策略提出了新要求.作为交通控制的应用前提，短时交通流预测研究具有重要的理论及现实意义.从研究思路来看，短时交通流预测主要包括基于确定的数据模型和无模型研究两种.前者的目标是利用确定的交通流模型，对交通运行状态的复杂变化进行准确描述，在此基础上利用各种算法对交通状态进行预测，例如多元回归模型[1]、ARIMA模型[2]、Kalman模型[3]以及由这些模型构成的各种组合预测模型；而后者的研究不需要确定的数学模型，仅仅依靠大量的先验数据，通过智能计算，完成交通流状态的迭代估计，例如支持向量机[4]、小波分析[5]、混沌理论[6]及神经网络[7- 10]相关的各种复合预测方法.基于确定性模型的交通流预测往往受制于模型自身，必须对实际情况进行适当简化，难以反映交通流运行的复杂特性，因此，通过改进预测算法，提高交通流模型的自适应性是研究难点.得益于计算机性能的大幅提高，无确定模型的预测方法不再受运算速度的制约，然而在未来的研究中，先验数据的筛选和目标函数的选取应当对交通流的运行特性加以考虑，提高预测结果的准确度，才能在实际中推广应用.

近年来，三相交通流理论的发展为短时交通流预测提供了新的思路，学者们在分析交通流参数的基础上，根据交通流的时空特性，对自由流和阻塞流的交通状态预测模型分别进行针对性研究，使预测效果得到有效提高[11- 12].另外，将交通流状态预测(流量、速度、密度等)和交通流模型参数预测(最大速度、最佳占有率等)进行结合研究，可实现模型参数与状态的实时估计和更新，使其准确跟踪交通流的运行特性，提高了模型的自适应性和预测精度[13].

卡尔曼滤波是经典的优化估计算法，通过反馈迭代完成参数预测，较为成熟并且适用性高，近年来，旨在改进卡尔曼滤波算法的研究成果不断涌现.Wang等[14- 15]基于扩展卡尔曼滤波对区域快速路网交通状态进行预测，分别利用仿真和实际数据对模型进行验证，取得了良好的效果.基于同样的交通流模型，袁磊等[16]利用正交差分的无损卡尔曼滤波对道路断面的交通流参数进行预测.朱征宇等[17]将支持向量机和卡尔曼滤波进行结合，提高了预测模型的稳定性和实时性.聂佩林等[18]研究了约束卡尔曼滤波组合预测模型在短时交通流预测方面的应用，并利用实际交通流数据进行了模型验证.文中以区域快速路网为研究对象，建立交通流状态空间模型，应用基于SVD的优化抗差无损卡尔曼滤波算法，对交通流运行状态和交通流模型参数进行综合预测，提高模型和算法的自适应性，以期达到良好的预测效果.

1 城市区域快速路网交通流建模

1.1 宏观交通流模型

Papageorgiou等[19]提出的二阶宏观交通流模型对快速路网从空间和时间上进行离散，描述交通流的运行动态.在该模型中，将路网离散为一系列长度为li的路段，如图1所示，用流量qi、速度vi、密度ρi来描述每个路段的运行特性，如果该路段包含出入匝道，则用ri、si分别代表该区段入口匝道和出口匝道的流量，其中i=1,2,…,N.q0、v0为路网入口交通流量和速度，ρN+1为路网出口交通流密度.同时，用周期T(T

图1 区域快速路网分解及交通特性示意图

Fig.1 Schematic diagram of regional freeway network decomposition and traffic characteristic

si(k)]

(1)

si(k)=βi(k)qi-1(k)

(2)

(3)

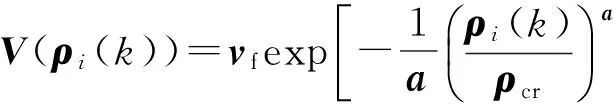
(4)

(5)

式(1)-(5)所示二阶宏观交通流模型对交通流密度、速度、流量的动态关系进行了完整表述，其中模型参数对路网变化不敏感，而最佳速度vf、最佳密度ρcr、指数参数a较为敏感，路网拓扑结构、环境因素不同，这三者都会有明显变化[15,20].文中选取的交通流模型是以流体力学模型为理论基础发展而来，有较大的参数规模、较高的复杂度，在描述三相交通流的变化趋势方面有较好表现，已经被验证能对实际交通流状态做出较为良好的预测[21].

1.2 交通流状态空间建模

以上述模型为基础，参照图1所示拓扑结构，构建交通流状态空间模型，对每一个路段的ρi(k)、vi(k)，快速路网的入口流量q0、速度v0，路网出口密度ρN+1，路段的入口匝道流量ri(k)，出口匝道流量占比βi(k)，以及路网模型参数vf、ρcr、a进行全面预测：

(6)

构建交通流特征变量z、边界变量b、模型参数p向量:

(7)

对于交通流特征变量z，预测状态与当前状态存在函数关系φ(·)，对于边界变量b和模型参数p，采用叠加噪声的一步预测方式获取下一时刻的状态.因此，状态空间表达式为

(8)

式中，ξ(k)均为叠加零均值高斯白噪声.假设在相邻路段的临界及路网边界都设有检测装置，则观测变量为

y=q1v1…qNvNq0v0r1…

rNβ1…βNT

(9)

进而得出观测方程

y(k)=g(x(k),η(k))

(10)

式中，η(k)为零均值高斯白噪声.

综上所述，得出宏观交通流系统状态空间模型：

(11)

2 无损卡尔曼滤波算法

传统的非线性滤波算法以扩展卡尔曼滤波(EKF)为代表，该算法通过对非线性模型进行Taylor展开，忽略高阶项，再结合经典的卡尔曼滤波进行状态估计，属于典型的函数近似法.然而，非线性函数的Jacobian矩阵求解计算量较大，在强非线性环境下精度降低，甚至会出现滤波发散，稳定性较差.无损卡尔曼滤波(UKF)是近年来提出的新型非线性滤波算法，该方法基于带有权值的样本集，通过无损变换(UT)估计非线性函数的概率密度分布，实现系统状态和协方差的非线性传递，对于滤波更新结果再利用经典卡尔曼滤波框架进行迭代运算，从而实现状态估计.UKF摒弃了函数近似法的理念，不存在高阶截断误差，不需要求导计算，较之EKF计算精度和稳定性都有所提高.

2.1 标准UKF算法

考虑系统的非线性状态方程和观测方程如式(11)所示，其中：x(k+1)和x(k)分别为k+1、k时刻的系统状态，y(k)为k时刻系统观测值，f(·)为状态模型，g(·)为观测模型，ξ(k)为过程噪声，η(k)为观测噪声，且满足：

(12)

UKF的计算步骤如下[22- 23]：

1)系统状态初始化

(13)

2)选取Sigma点

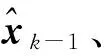
(14)

(15)

3)时间更新

Sigma点的非线性变换：

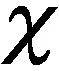
(16)

k时刻的状态向量预测均值：

(17)

k时刻的状态向量协方差阵：

(18)

4)测量更新

k时刻观测向量变换：

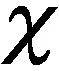
(19)

k时刻观测向量预测均值：

(20)

k时刻观测向量协方差阵：

(21)

5) 滤波更新

状态向量与观测向量协方差矩阵：

(22)

卡尔曼增益矩阵：

(23)

k时刻状态估计：

(24)

k时刻状态估计协方差阵：

(25)

滤波残差：

(26)

2.2 基于SVD的UKF算法

虽然UKF利用UT变换克服了EKF带来的截断误差和滤波发散问题，但是在实际应用中，系统状态先验信息矩阵的对称正定性并不能时刻得到保证，例如计算机的观测粗差、系统噪声等不确定性干扰，以及状态模型扰动异常等，都会破坏协方差矩阵的正定性，影响滤波器效果[22].另外，单纯通过抗差因子调节观测噪声矩阵的做法容易引起UT变换后观测向量协方差矩阵病态，降低UKF的滤波精度和稳定性.

UKF算法中的Sigma点选取环节，需要对协方差矩阵进行Cholesky分解，但是当协方差矩阵失去对称正定性时，滤波计算将无法进行.对于这种情况，可以采用奇异值分解(SVD)代替Cholesky分解.另外，非线性模型的复杂度越高，UT变换后越容易出现不确定的偏差，下文将介绍利用抗差因子对观测向量协方差矩阵和增益矩阵进行双向调节的改进算法，根据观测向量协方差矩阵的不同状态自适应确定抗差策略，该算法的流程如图2所示.

1)抗差因子

观测信息对滤波结果的贡献大小可以由抗差因子γ来调节，采用观测向量残差构建抗差因子，即

图2 基于SVD的改进抗差UKF算法流程图

Fig.2 Algorithm flow chart with improved resistance to error based on SVD-UKF

(27)

式中:k0、k1为阈值参数，通常k0取1.5～2.0，k1取3.0～8.5，两者取值越小，说明判定越严格，反之越宽松，文中取k0=2，k1=5[24];Svk为标准残差，计算公式为

(28)

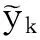
2)优化抗差SVD-UKF算法

为解决状态协方差矩阵非正定时无法进行Cholesky分解的问题，采用SVD分解计算Sigma点，即

(29)

值得说明的是,当Pk-1满足对称正定性时，两者的分解结果完全一致.

优化抗差算法的流程如图2所示，观测向量协方差的计算式为

(30)

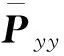
(31)

3 实验结果与分析

建立如图3所示路网拓扑结构，对前文所述的交通流状态空间模型和预测算法进行验证.在VISSIM仿真软件采集的交通流数据基础之上，利用Matlab完成交通流状态估计.参数设置见表1，选取3 h的预测时间，观测周期T=60 s，采用180组数据进行仿真实验.

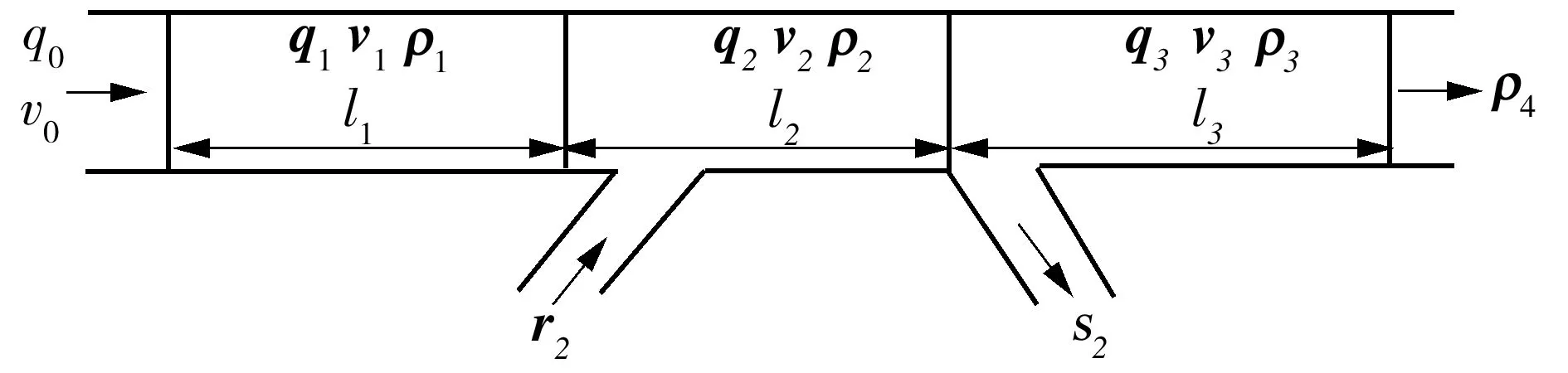
图3 路网拓扑结构图Fig.3 Network topology structure

参数类型参数设置路网参数l1=420m,l2=925m,l3=414m,1=2=3=3模型参数=20s,v=35km/h,κ=13veh/km,δ1=δ2=0.1过程噪声D(ξqi(k))=100veh/h,D(ξvi(k))=11km/h,i=1,2,3D(ξq0(k))=100veh/h,D(ξv0(k))=5km/h,D(ξρ4(k))=1.5veh/km/lane,D(ξr2(k))=3veh/h,D(ξβ2(k))=0.001,D(ξvf(k))=0.5km/h,D(ξρcr(k))=0.1veh/km/lane,D(ξa(k))=0.01测量噪声D(ηqi)=100veh/h,D(ηvi)=10km/h,i=0,1,2,3D(ηr2)=20veh/h,D(ηs2)=10veh/h

图4-7给出了部分状态变量的估计结果，可以看出预测结果能准确跟踪交通流状态的变化趋势.具体来说，交通流密度估计较为准确，而速度变量(v1、v2、v3、v0、vf)在某些时间点上存在明显的误差，流量相关的变量(q0、r2、β3)的估计较为准确，最佳密度(ρcr)的估计结果也在部分时刻出现了误差，但是在基准值的1/103水平上，可以忽略不计.

引入误差指标如均方根误差(RMSE)、平均绝对值百分比误差(MAPE)，在实验数据的基础上对EKF和SVD-UKF性能指标进行对比，结果见表2.

均方根误差：

(32)

平均绝对值百分比误差：

(33)

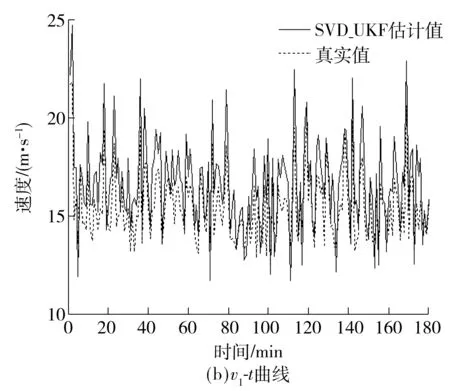
图4 路段1交通流密度ρ1、速度v1估计

Fig.4 Estimation of traffic flow density and speed of segment 1

从性能指标的对比结果来看，对于非线性程度较高的速度变量(v1、v2、v3，表2中用黑体显示)的估计，两个算法的RMSE均较高，但是SVD-UKF优于EKF.对于其他状态变量的估计，SVD-UKF的RMSE都比EKF提高了一个数量级.然而，MAPE的结果显示，对于速度变量(v1、v2、v3)的估计，SVD-UKF的MAPE稍逊于EKF，究其原因，相比于其他变量，速度状态模型的非线性更强，在某些时刻UT变换带来的转换误差非常大，速度估计相比原始值的偏差较大，而SVD-UKF算法的抗差设计并不能完全消除速度变量的不确定性误差，因此，在今后的研究中需要进一步改善.总体上来说，SVD-UKF算法在短时交通流状态预测方面的性能优于EKF算法.

表2 算法性能指标对比Table 2 Algorithm performance comparison

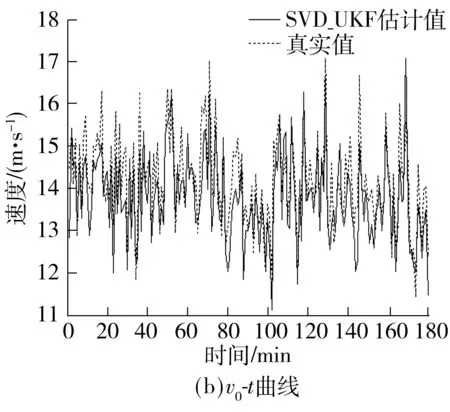
图5 快速路入口流量q0、速度v0估计Fig.5 Estimation of freeway entrance flow and velocity

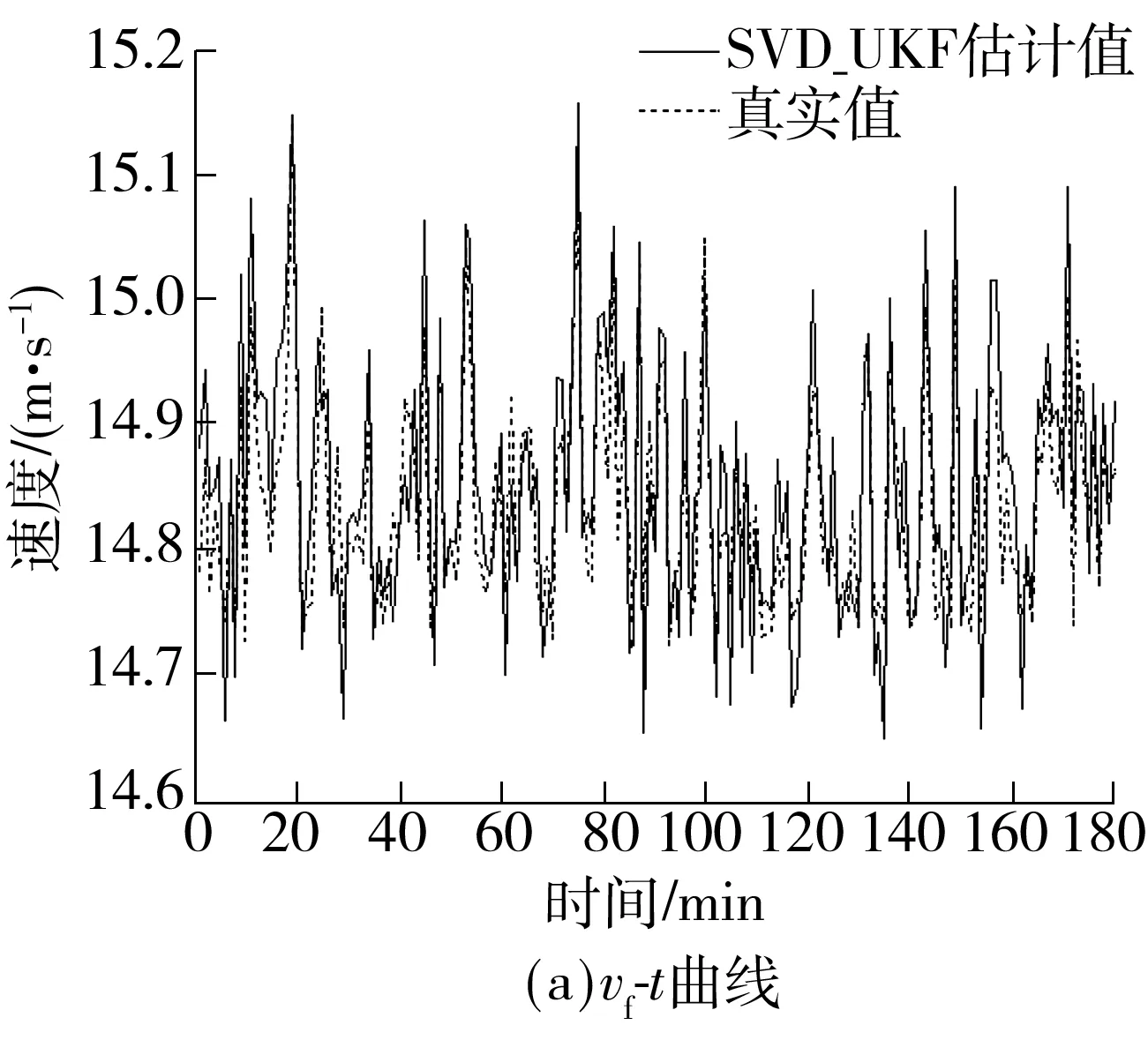
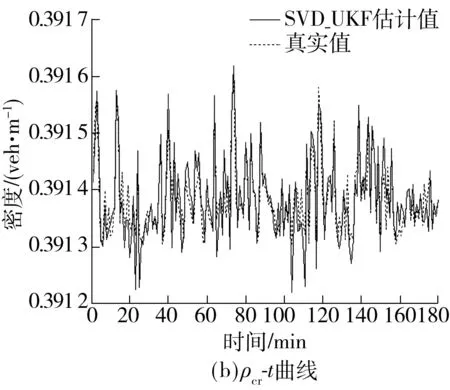
图6 模型参数最大速度vf、最佳密度ρcr估计

Fig.6 Estimation of model parameters maximum speed and the best density

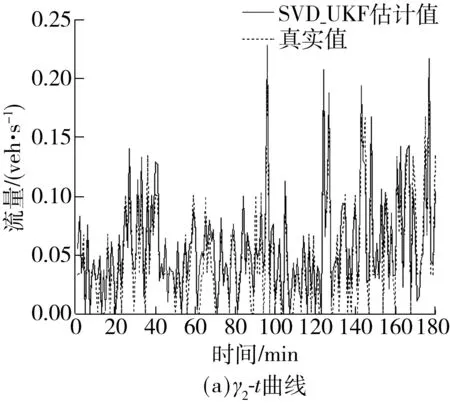
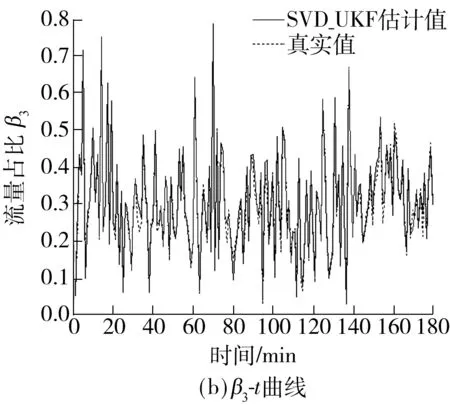
图7 入口匝道流量γ2、出口匝道流量占比β3估计

Fig.7 Estimation of the on-ramp traffic flow and off-ramp flow proportion

4 结语

文中针对城市区域快速路网，以实现交通流特征参数和模型参数的综合估计为目标，建立宏观交通流状态空间模型，对交通流状态和模型参数进行综合估计，提高模型适应性和预测精度.在标准UKF算法基础上，基于SVD的优化抗差UKF算法，用奇异值分解(SVD)代替标准UKF的Cholesky分解，在协方差矩阵非正定时，解决了滤波计算不能持续的问题，同时，该算法根据观测协方差矩阵是否病态自动选择抗差策略，对增益矩阵和观测协方差矩阵进行自适应计算，进而抑制由于模型较高的非线性带来的误差.实验证明，宏观交通流状态空间模型能准确跟踪交通流的动态变化，代价是较高的非线性和复杂度.相比于EKF，文中所提算法提高了交通流状态估计的稳定性和精度，今后将在模型参数优化和抗差算法设计方面做深入研究，以期将文中模型和算法在实际的交通流预测中推广应用.

[1] CLARK S.Traffic prediction using multivariate nonparametric regression [J].Journal of Transportation Enginee-ring,2003,129(2)：161- 168.

[2] WILLIAMS B M,HOEL L A.Modeling and forecasting vehicular traffic flow as a seasonal ARIMA process：theoretical basis and empirical results [J].Journal of Transportation Engineering,2003,129(6)：664- 672.

[3] ZHANG L,MA Y,SHI L.A hybrid traffic flow model for real time freeway traffic simulation [J].KSCE Journal of Civil Engineering,2014,18(4)：1160- 1164.

[4] 傅贵,韩国强,逯峰,等.基于支持向量机回归的短时交通流预测模型 [J].华南理工大学学报(自然科学版),2013,41(9)：71- 76. FU Gui,HAN Guo-qiang,LU Feng,et al.Short-term traffic flow prediction based on SVM regression model [J].Journal of South China University of Technology(Natural Science Edition),2013,41(9)：71- 76.

[5] LI T,SHENG L.Prediction for short-term traffic flow based on optimized wavelet neural network model [J].International Journal of Computer Science & Information Technology,2015,7(2)：183.

[6] 董春娇,邵春福,张辉,等.基于 GP 算法的快速路交通流参数相空间重构 [J].吉林大学学报:工学版,2012,42(3)：594- 599. DONG Chun-jiao,SHAO Chun-fu,ZHANG Hui,et al.Phase space reconstruction of traffic flow parameters on expressway based on G-P algorithm [J].Journal of Jilin University:Engineering and Technology Edition,2012,42(3)：594- 599.

[7] MIHAYLOVA L,BOEL R,HEGYI A.Freeway traffic estimation within particle filtering framework [J].Automatica,2007,43(2)：290- 300.

[8] KUMAR K,PARIDA M,KATIYAR V K.Short term tra-ffic flow prediction in heterogeneous condition using artificial neural network [J].Transport,2015,30(4)：397- 405.

[9] MEI H,MA A,POSLAD S,et al.Short-term traffic volume prediction for sustainable transportation in an urban area [J].Journal of Computing in Civil Engineering,2013,29(2)：04014036.

[10] 李松,刘力军,翟曼.改进粒子群算法优化 BP 神经网络的短时交通流预测 [J].系统工程理论实践,2012,32(9)：2045- 2049. LI Song,LIU Li-jun,ZHAI Man.Prediction for short-term traffic flow based on modified PS0 optimized BP neural network [J].Systems Engineering-Theory & Practice,2012,32(9)：2045- 2049.

[11] 董春娇,邵春福,诸葛承祥,等.基于时空特性的交通自由流短时预测状态空间模型 [J].土木工程学报,2013,46(8)：111- 118. DONG Chun-jiao,SHAO Chun-fu,ZHUGE Cheng-xiang,et al.A short-term state-space model for free flow prediction based on spatial-temporal characteristics [J].China Civil Engineering Journal ,2013,46(8)：111- 118.

[12] 董春娇,邵春福,周雪梅,等.基于交通流参数相关的阻塞流短时预测卡尔曼滤波算法 [J].东南大学学报(自然科学版),2014,44(2)：413- 419. DONG Chun-jiao,SHAO Chun-fu,ZHOU Xiao-mei,et al.Kalman filter algorithm for short-term jam traffic prediction based on traffic parameter correlation [J].Journal of Southeast University(Natural Science Edition),2014,44(2)：413- 419.

[13] PAPAGEORGIOU M,BLOSSEVILLE J M,HADJ-SALEM H.Modelling and real-time control of traffic flow on the southern part of Boulevard Peripherique in Paris：part I：Modelling [J].Transportation Research Part A：Gene-ral,1990,24(5)：345- 359.

[14] WANG Y,PAPAGEORGIOU M.Real-time freeway tra-ffic state estimation based on extended Kalman filter：a general approach [J].Transportation Research Part B：Methodological,2005,39(2)：141- 167.

[15] WANG Y,PAPAGEORGIOU M,MESSMER A.Real-time freeway traffic state estimation based on extended Kalman filter：adaptive capabilities and real data testing [J].Transportation Research Part A：Policy and Practice,2008,42(10)：1340- 1358.

[16] 袁磊,梁丁文,蔡之华,等.基于正交差分演化无迹卡尔曼滤波的短时交通流量预测算法 [J].计算机应用,2015,35(11)：3151- 3156. YUAN Lei,LIANG Ding-wen,CAI Zhi-hua,et al.Short-term traffic flow prediction algorithm based onorthogonal differential evolution unscented Kalman filter [J].Journal of Computer Applications,2015,35(11)：3151- 3156.

[17] 朱征宇,刘琳,崔明.一种结合 SVM 与卡尔曼滤波的短时交通流预测模型 [J].计算机科学,2013,40(10)：248- 251. ZHU Zheng-yu,LIU Lin,CUI Ming.Short-term traffic flow forecasting model combining svm and kalman filtering [J].Computer Science,2013,40(10)：248- 251.

[18] 聂佩林,余志,何兆成.基于约束卡尔曼滤波的短时交通流量组合预测模型 [J].交通运输工程学报,2008,8(5)：86- 90. NIE Pei-lin,YU Zhi,HE Zhao-cheng.Constrained Kalman filter combined predictor for short-term traffic flow [J].Journal of Traffic and Transportation Engineering,2008,8(5)：86- 90.

[19] PAPAGEORGIOU M,BLOSSEVILLE J M,HADJ-SALEM H.Macroscopic modelling of traffic flow on the Boulevard Périphérique in Paris [J].Transportation Research Part B：Methodological,1989,23(1)：29- 47.

[20] PAPAGEORGIOU M,BLOSSEVILLE J M,HAJ-SALEM H.Modelling and real-time control of traffic flow on the southern part of Boulevard Périphérique in Paris：part II：coordinated on-ramp metering [J].Transportation Research Part A：General,1990,24(5)：361- 370.

[21] WANG Y,PAPAGEORGIOU M,MESSMER A.Real-time freeway traffic state estimation based on extended Kalman filter：A case study [J].Transportation Science,2007,41(2)：167- 181.

[22] 高为广,何海波,陈金平.自适应 UKF 算法及其在 GPS/INS 组合导航中的应用 [J].北京理工大学学报,2008,28(6)：505- 509. GAO Wei-guang,HE Hai-bo,CHEN Jin-ping.An adaptive UKF algorithm and its application for GPS-INS integrated navigation system [J].Trans Beijing Ins Technol,2008,28(6)：505- 509.

[23] 曲从善,许化龙,谭营.一种基于奇异值分解的非线性滤波新算法 [J].系统仿真学报,2009,21(9)：2650- 2653. QU Cong-shan,XU Hua-long,TAN Ying.New nonlinear filtering algorithm based on svd [J].Journal of System Simulation,2009,21(9)：2650- 2653.

[24] 杨元喜.自适应动态导航定位 [M].北京:测绘出版社,2006：99- 101

Application of SVD-Based Optimized Robust UKF Algorithm to Estimation of Short-Term Traffic Flow State

XULun-huiWANGXiang-xue

(School of Civil Engineering and Transportation, South China University of Technology, Guangzhou 510640, Guangdong, China)

In order to realize the real-time traffic flow state estimation of the regional freeway network in cities, a macroscopic traffic flow state space model is constructed. This model helps to estimate the traffic flow states and update the model parameters, and it can improve the adaptability and accuracy of the traffic flow model. Then, the SVD(Singular Value Decomposition)-based optimized robust UKF(Unscented Kalman Filter) algorithm is proposed. In the algorithm, the singular value decomposition is adopted to replace the Cholesky decomposition, thus solving the problem that the filtering can’t continue when the covariance matrix is non-positive. Meanwhile, different strategies are chosen according to whether the observation covariance matrix is pathological, and both the gain matrix and the observation covariance matrix are adaptively calculated. Furthermore, the error caused by the high nonlinearity of the constructed model is inhibited.Experimental results show that the proposed algorithm can avoid the filtering divergence of the EKF(Extended Kalman Filter) algorithm and can accurately track the trend of the traffic flow, thus improving the stability and precision of the traffic flow state estimation.

traffic flow state space model; UKF algorithm; singular value decomposition; error resistance factor

2016- 04- 22

国家自然科学基金资助项目(61263024) Foundation items: Supported by the National Natural Science Foundation of China(61263024)

许伦辉(1965-)，男，教授，博士生导师，主要从事智能交通系统理论及应用、交通流系统建模与仿真等研究.E-mail:lhxscut@163.com

1000- 565X(2016)12- 0044- 09

U 491

10.3969/j.issn.1000-565X.2016.12.007