高速公路景观色彩对驾驶人脑电α/β值的影响*

王琳虹

(吉林大学 交通学院∥汽车工程学院， 吉林 长春 130025)

高速公路景观色彩对驾驶人脑电α/β值的影响*

王琳虹

(吉林大学 交通学院∥汽车工程学院， 吉林 长春 130025)

为量化高速公路路侧景观色彩与驾驶人脑电α/β值之间的关系，在吉珲高速公路进行道路试验采集所需数据.基于双指数函数建立景观色彩值与脑电α/β值的关系模型.考虑到驾驶时间对驾驶人脑电α/β值的累积影响，基于三次高斯函数建立驾驶时间与脑电α/β值的关系模型.最后采用联合建模的方式建立驾驶时间、景观色彩值对脑电α/β值的关系模型.模型分析结果表明：路侧景观色彩均值与驾驶员脑电α/β值呈负相关，随着色彩值的增大即景观色彩越加明亮、鲜艳，驾驶员的α/β值越趋近于1，即达到放松与警惕之间的平衡状态；驾驶员脑电的α/β值随着驾驶时间呈现波动，驾驶员的主观意识强迫自己要时刻处于警醒状态，驾驶员自身会存在精神放松与警醒的博弈过程.研究结果可为考虑驾驶疲劳的高速公路景观色彩设计提供理论基础.

交通运输安全工程；高速公路；景观色彩；驾驶时间；脑电；α/β值

高速公路景观对驾驶人的影响体现在两方面.一方面是偶发性的影响，如道路上设置的非交通标志广告牌、强反射光、进出隧道时光强的突变等均易对驾驶人造成视觉干扰，分散其注意力，带来安全隐患.另一方面是累积性的影响，如路侧景观的色彩、连续性、植被造型及间距等通过长时间作用于驾驶人的生理、视觉，可能引起驾驶人注意力、反应速度等疲劳特性的变化，进而影响驾驶人的操纵能力.无论是累积性还是偶发性的影响，最后均有可能诱发交通事故.偶发性影响因素所导致的交通事故常常易被发现，能够引起管理者的关注，并进行控制或者预防.而高速公路路侧景观通过长时间作用对驾驶疲劳所产生的累积性影响导致操纵能力下降却不易被发现，遭到管理者的忽视.脑电常作为评价驾驶疲劳的主要生理指标，因此研究高速公路路侧景观对驾驶人脑电特征参数的影响规律具有重要的科学意义，可为考虑驾驶疲劳的高速公路景观的设计提供合理依据.

人体任何细微的动作及心理变化均可以在脑电中有所体现，利用脑电(EEG)监测驾驶人是相对客观、精确的方法之一.高速公路上路侧景观的色彩对驾驶人视觉及心理产生刺激，进而反映在脑电波中.人类脑电图中脑波频率一般在1～30 Hz，根据频带不同可以将脑电波划分为α、β、θ、δ4个节律.其中α节律多在驾驶人精神放松的时候出现[1- 6]，α节律的功率谱密度积分成分α值可以表示驾驶人精神上放松的程度；而β节律多在驾驶人精神警醒的时候出现[1- 4,7- 8]，β节律功率谱密度积分的成分β值可以表示驾驶人精神的警醒程度；那么，α/β值(以下均简称为脑电α/β值)可以表示驾驶人的状态是更倾向于放松还是警醒.因此文中研究路侧景观对驾驶人脑电α/β值的影响，以期为进一步研究路侧景观对驾驶疲劳的影响奠定基础.

当前有关高速公路景观色彩等景观自身特性对驾驶人的心电、脑电等生理指标的研究较少.李香红等[5]研究了不同景观路段下驾驶人心率、心率增长率的变化规律，并对心率增长率与行驶时间、心率增长率与行驶速度进行了相关性分析，结果表明不同景观路段导致驾驶人在相同实验条件下的生理指标存在差异；朱翠翠[6]通过行车试验，研究了道路圆曲线半径和坡度与脑电信号β波绝对功率值的相关性，结果表明驾驶人在从直线路段进入到圆曲线路段和上坡坡度时，驾驶人的β波绝对功率值与圆曲线半径呈负相关，与上坡坡度值呈正相关；而国外相关领域学者没有对景观色彩对驾驶人生理特性的影响关系进行研究.

综上所述，目前景观对驾驶人生理的影响研究也仅局限于定性分析景观植被间距、公路弯道半径对驾驶人生理特性的影响[9- 11]，而没有从景观色彩等自身特性角度出发进行研究.路侧景观只有在长时间尺度内才会对驾驶疲劳产生累积影响，在累积过程中无法忽略驾驶时间的作用.因此文中建立驾驶持续时间、景观的色彩均值共同影响下的脑电α/β值的预测模型.为后续研究考虑驾驶疲劳的高速公路景观设计提供研究基础.

1 实车道路试验与数据预处理

为研究高速公路路侧景观色彩与脑电α/β值的关系，课题组在吉珲高速公路进行实车道路试验，采集路侧景观图像及相关驾驶人脑电相关参数.

1.1 试验设计

为确保路侧景观色彩的多样性，课题组在夏季与秋季分别在吉珲高速公路进行为期两天的实车道路实验，每天的试验时间为6:00-18:00，具体景观如图1所示.要求驾驶人状态良好，驾驶经验丰富，年龄范围为35～45岁.试验采用美国Biopac公司的MP100 16导生理记录仪采集驾驶人的脑电生理指标；利用数码相机采集高速公路路侧景观视频.实车道路试验相关情况如图2所示.

影响驾驶疲劳的主要因素包括驾驶持续时间、公路景观、道路交通状态及道路线形4个方面.由于吉珲高速公路上的交通量很小，驾驶人受高速公路上相邻车辆的影响较小，因此道路交通状态因素可以忽略不计.实验选择的吉珲高速公路为道路线形既不平直单调也没有急弯斗坡的路段，驾驶人受道路线形的影响较小，因此也可剔除道路线形这一影响因素.根据经验可知：在驾驶人行车过程中，短时(如几秒或者几分钟)的路侧景观变化难以对驾驶人的生理特性产生影响，但是随着驾驶时间的逐渐增加，路侧景观的单调性或者色彩突变将会对驾驶人产生作用，甚至造成驾驶人疲劳.因此本次实车道路试验时间较长，采集的景观视频及驾驶人脑电生理指标数据量较多.

图1 夏季与秋季的路侧景观

Fig.1 Typical roadside landscape in summer and autumn

图2 实车道路试验相关情况Fig.2 Field vehicle experiment condition

1.2 数据预处理

实验中采集了40 h左右的高速公路景观及驾驶人的生理指标数据.考虑驾驶疲劳的累积特性，从中选择了连续驾驶3 h的实验数据作为研究对象.剔除了驾驶人休息次数过多、路侧景观色彩不丰富、天气恶劣(下雨)时行驶路段的实验数据.

实验采集的景观视频速率为30帧/s，而景观色彩对驾驶人的影响是长时间的累积作用，不会几秒之内便对驾驶人产生影响.因此选择30 s作为图像采集间隔，即每半分钟提取一幅景观图像.基于Biopac的生理记录仪采集频率为1 000 Hz，为了使得两组数据一一对应，也选择每半分钟提取一组脑电指标.

视频图像处理：将采集的景观视频解压为图片序列并每半分钟提取一副图片.基于图像分割中的纹理分析方法提取高速公路路侧景观，并基于k-均值聚类提取路侧景观主体色彩并计算景观色彩值[12].用符号C表示景观的色彩值，C的计算方法为：C=65 536B+256G+R,R、G、B为红色、绿色、蓝色等3个通道颜色值[13].

生理数据处理：根据引言中的论述，选择脑电α/β值表征驾驶人的生理特性.

因数据量较大，选择Matlab对脑电数据进行波形处理.试验中采集的脑电信号均为时域信号，为了获取脑电不同波形的功率谱密度，需要利用傅里叶变换将脑电时域信号转换为频域信号.然后根据脑电α波、β波的不同频率范围进行滤波.最后对过滤后的波形进行功率谱密度分析，进而利用微分的思想求得不同节律脑电波的功率谱密度积分.

2 考虑驾驶时间的景观色彩对脑电α/β值的影响关系建模

首先考虑驾驶时间、景观色彩对脑电α/β值的影响，建立表达模型；然后为研究高速公路路侧景观、驾驶时间对驾驶人脑电α/β值的联合影响规律，选择路侧景观的色彩值、驾驶时间作为自变量，脑电α/β值作为因变量建立三者之间的联合关系模型.

景观色彩值与脑电α/β值的数量级相差非常大，导致建模中存在很多问题，因此对数据进行归一化处理，计算公式如下：

(1)

2.1 驾驶时间对脑电α/β值的影响

1)数据分析

为了拟合驾驶时间与驾驶人α/β值的关系，首先绘制驾驶时间与α/β值的散点图，如图3所示.

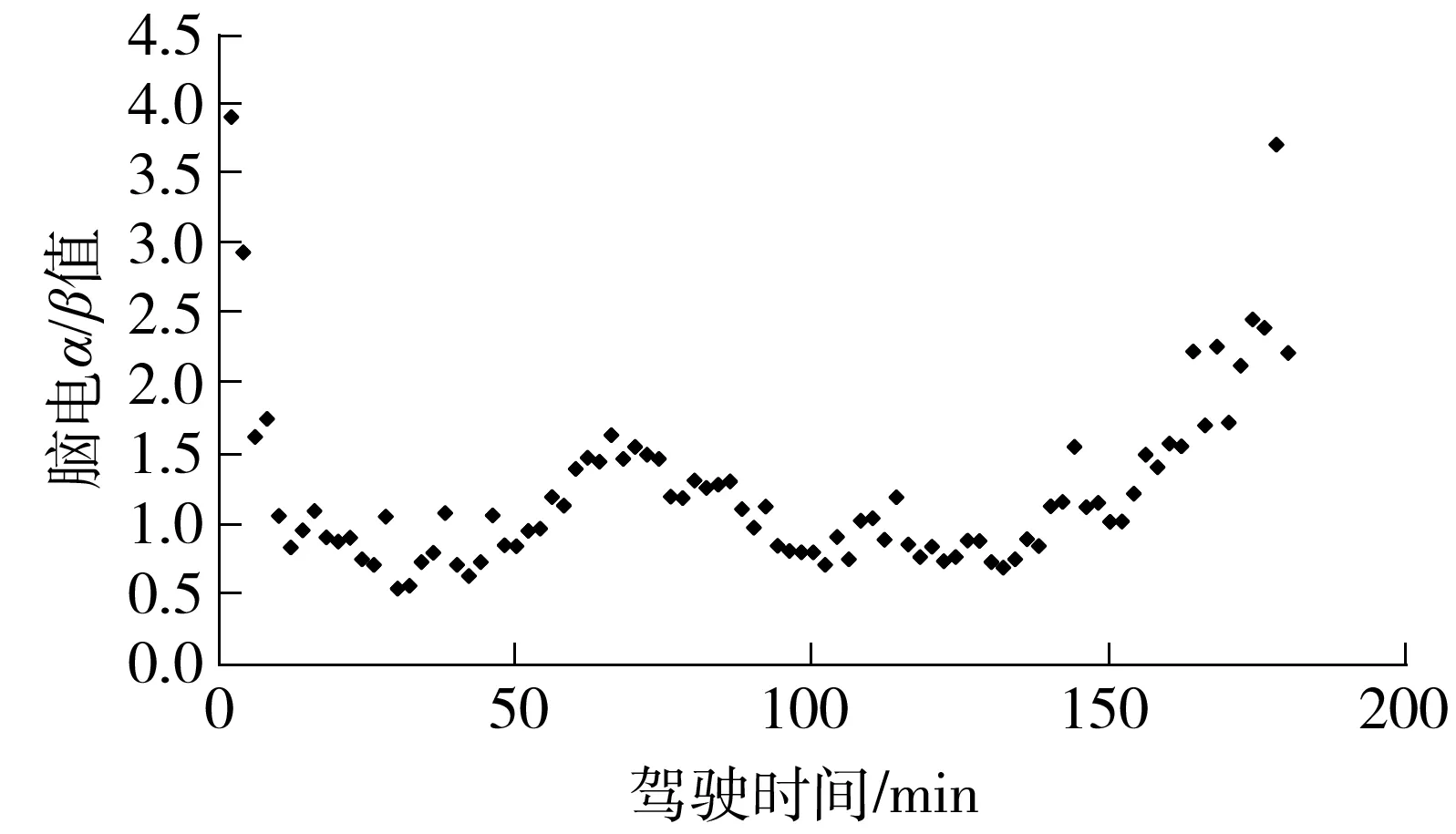
图3 驾驶时间与脑电α/β值的散点图

Fig.3 Scatter diagram between driving time andα/βvalue of EEG

脑电α/β值可以表示驾驶人的状态更倾向于放松还是警醒.

观察图3可以发现：在驾驶过程初期，α/β值达到4左右，说明此时驾驶人脑电α值远大于β值，驾驶人处于精神放松的状态；之后随着驾驶时间的延长，α/β值快速变小，甚至小于1，说明驾驶人逐渐进入了高度警醒的状态；长时间的精神紧张不会维持过久，在第40 min左右α/β值逐渐升高，说明驾驶人又逐渐恢复了精神放松的状态.这种变化过程体现了人体的自我调节能力.此外，由于高速公路上驾驶比较危险，驾驶人的主观意识强迫自己要时刻处于警醒状态，驾驶人自身会存在精神放松与警醒的博弈过程，因此在图3中α/β值呈现了周期波动的现象.

2)模型建立及检验

观察驾驶时间与脑电α/β值的散点图，发现二者的变化趋势符合三次高斯函数形式.三次高斯函数的形式为

(2)

式中,ai、bi、ci(i=1，2，3)均为待拟合参数.

利用三次高斯函数对二者的关系式进行拟合，拟合模型参数结果为：a1=4.732×e13，b1=-370.4，c1=67.75；a2=48.43，b2=382.6，c2=120.2；a3=1.24，b3=67.61，c3=47.67.则驾驶时间t对脑电α/β值的影响关系模型为：

(3)

式中,t为驾驶时间.

拟合模型的判定系数r2=0.855，表明自变量与因变量的相关性较大，模型的回归效果较好.

拟合模型中自变量与因变量的关系曲线如图4所示.

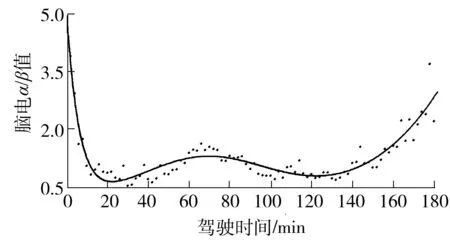
图4 驾驶时间与脑电α/β值的影响关系拟合曲线Fig.4 Fitting curve between driving time and α/β value of EEG

2.2 景观色彩对脑电α/β值的影响

1)数据分析

为了建立景观色彩对脑电α/β值的影响关系模型，首先绘制二者之间的散点图，如图5所示.

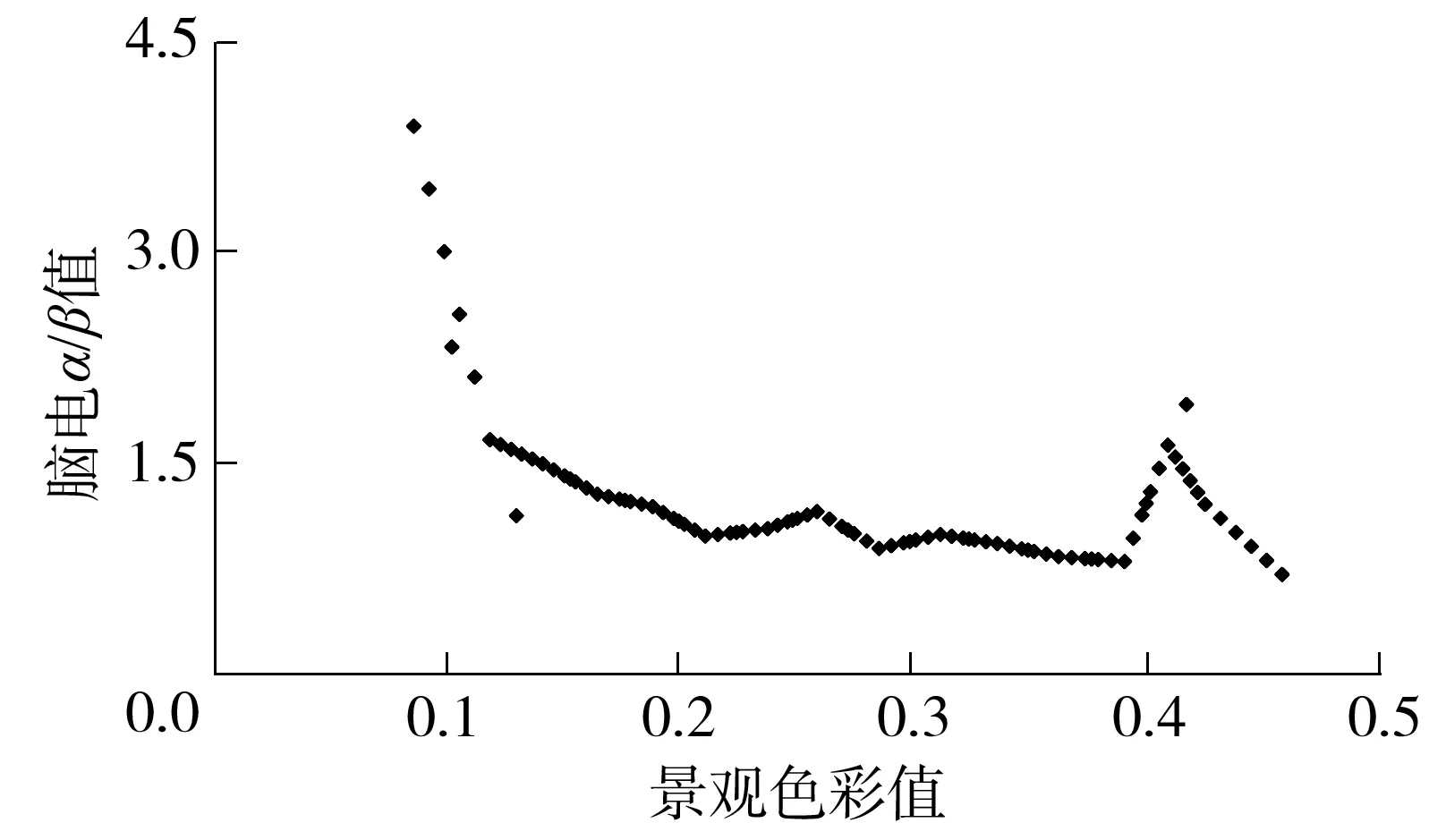
图5 景观色彩值与脑电α/β值的散点图

Fig.5 Scatter diagram between landscape color andα/βvalue of EEG

从图5可看出,随着色彩值的增大(即景观色彩越加明亮、鲜艳)，驾驶人的α/β值趋近于1，即达到放松与警惕之间的平衡状态.而这说明景观色彩越明亮，驾驶人的精神状态越处于放松与警醒的平衡状态.

经分析发现，当路侧景观色彩值小于0.2时，驾驶人脑电α/β值较大且随着景观色彩值的增加而快速下降，说明景观色彩偏暗时(多为灰色的水泥边坡、灰褐色的泥土边坡以及收割后的耕地等单调、枯燥的景观)，驾驶人脑电α/β值远大于1，即脑电α波的成分远多于β波的成分，此时大脑处于比较放松或者低速运行状态，说明单调枯燥的景观可以使驾驶人精神懈怠，如遇突发事故可能无法及时做出响应.

当路侧景观色彩值大于0.2时(即景观颜色越加明亮、鲜艳，如夏季绿色的植被、秋季橙黄色的针叶林等)，驾驶人的α/β值趋近于1，即脑电α波的成分与β波的成分接近，此时驾驶人处于放松与警醒的平衡状态，是驾驶人比较理想的驾驶状态，既不会因为过于放松而无法及时应对突发事故，也不会过于紧张导致疲劳的加速.散点图中间波动部分可能是受到外界突发的刺激而产生的，比如超车、换道等.

2)模型建立及检验

观察景观色彩与脑电α/β值的散点图，发现二者关系可以采用双指数函数进行表达，即

α/β=a1eb1x+a2eb2x

(4)

式中：ai、bi(i=1，2)均为待拟合参数.

采用散点图中的数据拟合景观色彩值C与脑电α/β值的关系式，拟合参数为：a1=110.7，b2=-42.88，a2=1.167，b2=-0.333 2.那么二者的关系模型为

α/β=110.7e-42.88C+1.167e-0.333 2C

(5)

拟合模型的判定系数r2=0.917 7，表明拟合效果较好.景观色彩值C与脑电α/β值的拟合曲线如图6所示.

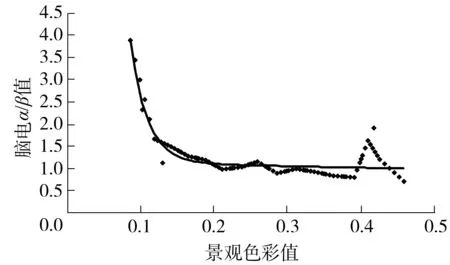
图6 景观色彩值对α/β值的影响关系拟合曲线

Fig.6 Fitting curve between landscape color andα/βvalue of EEG

2.3 考虑驾驶时间的景观色彩对脑电α/β值的影响

1)基于迭代的模型融合

在实际情况中，驾驶时间与景观色彩共同作用于脑电α/β值.因此还需建立以驾驶时间、景观色彩为自变量，驾驶人α/β值为因变量的关系模型.

在2.1和2.2节已经分别建立了驾驶时间、景观色彩对α/β值的影响关系模型，在这两个模型中，自变量与因变量呈非线性关系，因此无法通过简单的线性叠加融合两个模型.文中采用变量替换法将非线性问题线性化.

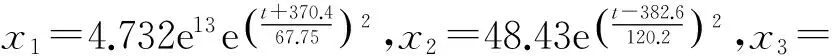
α/β=β1x1+β2x2+β3x3+β4x4+β5x5+β6

(6)

式中，βi(i=1，2，…,6)为待拟合参数.

模型参数标定过程如下：

①将所有的样本C和t代入计算出的x1，x2，…x5中，并计算出其对应的脑电α/β值.

②利用Matlab中的Curve Fitting Tool工具箱对式(6)进行多元线性回归，得到拟合模型的参数为：β1=0.748，β2=0.556，β3=0.117，β4=0.081，β5=3.553，β6=-3.321.

③得到最终的多元回归模型：

α/β=0.748x1+0.556x2+0.117x3+0.081x4+

3.553x5-3.321

(7)

将拟合模型中的x1，x2，…,x5还原为t、C，得到景观色彩、驾驶时间与脑电α/β值的关系模型：

4.146e-0.333C-3.321

(8)

2)模型验证

为了评价模型拟合效果，分别对模型拟合优度进行相关性检验和显著性检验.F检验通过利用变量z的总离差平方和中剩余平方和与回归平方和的比值，检验回归模型整体的显著性.对回归模型进行r2检验以及F检验并能够检验通过，方可应用拟合模型.

①回归模型的相关检验

回归模型的相关性检验是对模型的精度减小验证，并决定拟合模型是否可应用于研究中.

拟合模型的r2=0.852，表明判定系数较大、模型的回归效果较好.

②F检验

为了判别拟合模型输出的脑电α/β值与实际采集到的脑电α/β值是否存在显著差异，对两组数据进行F检验.选择显著性水平0.05，5自由度的拟合函数，样本量为168，查表得F0.05(5,∞)=2.21.而根据两组数据方差计算得到的F值为129.671，远大于F临界值，拟合方程通过F检验.

综上可判断所建模型能有效地表达高速公路路侧景观色彩值、驾驶时间与脑电α/β值的关系.

3 敏感性分析

3.1 敏感性分析方法选择

为了研究随着路侧景观色彩值C、驾驶时间t的变化，驾驶人脑电α/β值变化的幅度，对所建模型进行敏感性分析.敏感性分析包括单因素敏感性分析和多因素敏感性分析.单因素敏感性分析仅研究某一个参数变化对目标的影响，而多因素敏感性分析需要考虑各种因素组合变动对目标的影响.单因素与多因素敏感性分析的区别在于是否考虑各参数之间的相互作用[14].因驾驶时间与景观色彩无相互作用，因此选择单因素敏感性分析.

3.2 单因素敏感性分析

敏感度系数是在影响因素作用下目标值变化百分比与该影响因素变化百分比的比值.敏感度系数高代表目标对影响因素的敏感程度高，反之敏感程度低.敏感度系数计算公式如下：

E=ΔH/ΔF

(9)

式中:E为敏感度系数；ΔF为影响因素F的变化率，%；ΔH为影响因素发生变化时目标的相应变化率，%.

E>0表示目标与影响因素同方向变化，E<0表示目标与影响因素朝相反方向变化.在本节将驾驶人生理指标脑电α/β值作为评价指标，驾驶时间、景观色彩作为影响因素；以拟合关系模型(8)为基础，研究在固定一个影响因素的情况下，各个指标对另一个影响因素的敏感程度.

脑电α/β值对景观色彩值C、驾驶时间t的敏感系数如表1所示.以一个场景为例测试了景观色彩值C、驾驶时间t以10%为步长、上下变化30%情况下脑电α/β值的变化率，进而得到脑电α/β值指标对影响因素的敏感系数E(α/β).

表1显示，随着驾驶时间t增幅的变化，脑电α/β值的增量幅度相对较大，即脑电α/β值对驾驶时间t的敏感程度相对较大，表明驾驶时间会影响驾驶人大脑的活动活跃程度以及放松、警醒程度.驾驶时间t与驾驶人脑电α/β值呈正相关，即驾驶时间越长，脑电α/β值越大，亦即驾驶人大脑中α节律越多，大脑运转速度及活跃程度降低.

表1 驾驶人脑电α/β值对景观色彩值的敏感性分析结果

Table1Sensitiveanalysisresultsoftheα/βvalueofdriver’sEEGtolandscapecolor

c增量/%α/β增量/%E(α/β)t增量/%α/β增量/%E(α/β)10-2.01-0.2010100.250.024720-3.98-0.1990200.420.021130-5.91-0.1970300.540.0179-102.06-0.2056-10-0.320.0318-204.16-0.2079-20-0.690.0346-306.30-0.2101-30-1.080.0359

由表1还可看出，景观色彩值C与驾驶人脑电α/β值呈负相关，且随着景观色彩C值增幅的变化，脑电α/β值的增量幅度较大，即脑电α/β值对驾驶时间t的敏感程度较大，且远大于其对景观色彩C的敏感程度，说明景观色彩是影响驾驶人脑部活跃程度的主要因素.

4 结论

文中首先基于双指数函数建立景观色彩值与脑电α/β值的关系模型.然后考虑到驾驶时间对驾驶人脑电α/β值的累积影响，基于三次高斯函数建立驾驶时间与脑电α/β值的关系模型.最后采用联合建模的方式建立驾驶时间、景观色彩值对脑电α/β值的影响关系模型.研究结果如下：①路侧景观色彩值c与驾驶人脑电α/β值呈负相关，随着色彩值的增大(即景观色彩越加明亮、鲜艳)，驾驶人的α/β值趋近于1，即达到放松与警惕之间的平衡状态；②驾驶人脑电的α/β值随着驾驶时间t呈现波动，其原因为驾驶人的主观意识强迫自己要时刻处于警醒状态，驾驶人自身会存在精神放松与警醒的博弈过程；③敏感性分析结果表明驾驶时间、景观色彩对驾驶人脑电α/β值存在不同程度的影响，其中前者的影响程度要高于后者的影响程度，说明景观色彩是影响驾驶人脑部活跃程度的主要因素.

后续研究基于脑电信号的驾驶疲劳判别方法、高速公路路侧景观对驾驶疲劳的综合影响机理.科学设计高速公路路侧景观奠定基础.

[1] 吴绍斌,高利,王刘安.基于脑电信号的驾驶疲劳检测研究 [J].北京理工大学学报,2009，29(12):1072- 1075. WU Shao-bin,GAO Li,WANG Liu-an.Detecting driving fatigue based on electroencephalogram [J].Transactions of Beijing Institute of Technology,2009,29(12):1072- 1075.

[2] 莫雄强.基于脑电的疲劳度检测方法研究 [D].秦皇岛：燕山大学电气工程学院,2009.

[3] QU Xiao-bo,YANG Ying,LIU Zhi-yuan,et al.Potential crash risks of expressway on-ramps and off-ramps:a case study in Beijing,China [J].Safety Science,2014,70:58- 62.

[4] QU Xiao-bo,KUANG Yan,ERWIN Oh,et al.Safety eva-luation for expressways:a comparative study for macroscopic and microscopic indicators [J].Traffic Injury Prevention,2014,15(1):89- 93.

[5] 李香红，朱守林，戚春华．基于不同公路景观环境的驾驶员生理反应实验研究 [J]．内蒙古农业大学学报(自然科学版)，2010，31(4)：172- 176 LI Xiang-hong,ZHU Shou-lin,QI Chun-hua.Experiment research on influence about the different road environment on drivers’ physiology reaction [J].Journal of Inner Mongolia Agricultural University(Natural Science Edition),2010,31(4):172- 176.

[6] 朱翠翠.驾驶员脑电特性与山区双车道公路线形相关性研究 [D].成都：西南交通大学交通运输与物流学院,2013.

[7] 李影洁，邱意弘，朱贻盛．脑电信号分析方法及其应用 [M]．北京：科学出版社，2009．

[8] JAP B T,LAL S,FISCHER P,et al.Using EEG spectral components to assess algorithms for detecting fatigue [J].Expert Systems with Applications,2009,36(2):2352- 2359.

[9] LI Shi-wu,WANG Lin-hong,YANG Zhi-fa.A driver fatigue recognition model using multiple physiological features based on support vector machine [J] Information Journal,2012,15(12):5321- 5328.

[10] JAP B T,LAL S,FISCHER P.Comparing combinations of EEG activity in train drivers during monotonous driving [J].Expert Systems with Applications,2011,38:45- 53

[11] PARTIN D L,SULTAN M F,THRUSH C M,et al.Monitoring driver physiological parameters for improved safety [R].Detroit:SAE,2006:76- 79

[12] 李世武，王琳虹，杨志发，等.高速公路路侧景观提取及量化研究 [J]．吉林大学学报(工学版)，2011，41(4):956- 962. LI Shi-wu,Wang Lin-hong,Yang Zhi-fa,et al.Feature quantification method for freeway roadside landscape [J].Journal of Jilin University(Engineering and Technology Edition),2011,41(4):956- 962.

[13] 何韵旺.色彩基础 [M].北京:北京理工大学出版社，2009.

[14] 秦伟，朱守林，戚春华.草原公路驾驶室噪声与驾驶员心率变异指标敏感性研究 [J].内蒙古农业大学学报(自然科学版)，2011,32(3):246- 249 QIN Wei,ZHU Shou-lin,QI Chun-hua.The research about prairie road cab noise environment and sensitivity of driver heart rate variability [J].Journal of Inner Mongolia Agricultural University(Natural Science Edition),2011,32(3):246- 249.

Impacts of Roadside Landscape Color of Freeways onα/βValue of Driver’s EEG Signal

WANGLin-hong

(School of Transportation∥College of Automotive Engineering,Jilin University, Changchun 130025, Jilin, China)

In order to quantify the relationship between the roadside landscape color of freeways and theα/βvalue of the driver’s EEG signal, real vehicle experiments were conducted in Jilin-Hunchun freeway to collect the data. Based on the double exponential function, a relationship model between the landscape color and theα/βvalue of the driver’s EEG signal was constructed. Then, by considering the cumulative impact of the driving time on theα/βvalue, their relationship model is constructed based on the cubic Gaussian function. Finally, a model describing the relationships of the driving time and the landscape color to theα/βvalue was constructed by means of the joint modeling method. Model analysis results show that the landscape color is negatively correlated with theα/βvalue, i.e. with the increase in the brightness of the landscape color, theα/βvalue approaches to 1, which indicates a balance between the relaxed state and the alert state, and that there is a fluctuating relationship between the driving time and theα/βvalue, specifically, when a driver forces himself into an alert state, there is a game between falling into fatigue and resisting fatigue. The findings can provide a theoretical basis for the landscape color design considering the driving fatigue.

traffic and transportation safety engineering; freeways; landscape color; driving time; EEG signal;α/βvalue

2015- 12- 07

国家自然科学基金资助项目(51308251)；中国博士后科学基金资助项目(2013M541306) Foundation items: Supported by the National Natural Science Foundation of China(51308251) and China Postdoctoral Science Foundation(2013M541306)

王琳虹(1984-)，女，博士后，副教授，主要从事交通环境与安全技术研究.E-mail:wanghonglin0520@126.com

1000- 565X(2016)12- 0061- 06

U 491.2

10.3969/j.issn.1000-565X.2016.12.009