基于离散变量GA-APSO算法的钢结构优化分析

郝润霞,袁帅,赵根田

内蒙古科技大学建筑与土木工程学院,内蒙古包头014010

基于离散变量GA-APSO算法的钢结构优化分析

郝润霞,袁帅*,赵根田

内蒙古科技大学建筑与土木工程学院,内蒙古包头014010

本文针对遗传算法和粒子群算法收敛早熟、局部搜索能力差等缺点，在改进速度与位置更新算子函数的粒子群算法的基础上，插入了遗传算法的交叉和变异算子，提出了一种新的启发式现代混合算法——遗传-加速粒子群混合算法(GA-APSO)。该算法可以很好的跳出局部最优，扩大搜索域范围，提高收敛速度进而得到更合理的最优解。并基于离散变量将映射函数插入GA-APSO算法中，衍生出一种基于离散变量的GA-APSO算法，以一榀框架为算例通过与基于离散变量的APSO算法进行对比分析，证明了该衍生算法对于检索截面数据库中型钢规格自动选取具有一定的适用性。

GA-APSO算法;钢结构;优化设计

当下的科学技术处于一个相互交叉、渗透和影响的时代。随着计算机技术的发展，数学规划和运筹学一直是非常活跃的领域。它们能与实际工程问题联系到一起通过计算机达到多学科相互联系的目的。结构优化设计的产生与发展正是将工程、力学、数学与计算机应用等领域交叉结合的产物。钢框架结构的最优化设计越来越受到研究人员的重视，在过去的几十年里国内外不少学者将不同的优化技术和算法应用于结构优化中。钢框架结构的最优化设计的目的是在保证满足相关规范的约束下，以改变钢构件截面尺寸的方式使得钢框架的整体自重达到最轻，从而拥有更好的经济性。

其中粒子群算法(Particle Swarm Optimization)[1]是Kennedy和Eberhart在1995年提出的一种启发式智能优化算法。文献[2]提出了一种连续变量的加速粒子群算法(Acceleration based Particle Swarm Optimization)，该算法相比传统的粒子群算法，具有收敛快、不容易早熟等特点[3]。但是在实际的工程优化问题中往往伴随着设计变量离散性、约束条件非线性、不可微性等等，这些特性决定了工程结构优化问题上的复杂性[4]。本文将加速粒子群算法和另一种启发式算法——遗传算法（Genetic Algorithms）[5]相结合，提出一种混合算法：即粒子群遗传混合算法（GA-APSO Algorithms）。它在APSO算法的基础上，插入了GA算法的交叉和变异算子提高了粒子群算法的全局搜索性能；通过对APSO算法的速度更新公式的改进提高算法的收敛速度；并且通过将离散变量映射成连续函数的方法，使其可以与数据库中的截面尺寸进行匹配从而达到在优化设计中快速自选最优截面的目的。

1 离散变量的GA-APSO混合算法

1.1 GA-APSO混合算法的基本原理

遗传-粒子群混合算法（GA-APSO）在APSO算法的基础上保留了粒子群算法的搜索速度快、算法简单和适用于实值型问题处理等优点；插入了遗传算法中的交叉和变异算子增加了算法的搜索能力，进一步提高了种群的多样性，从而减小了两种算法共有的早熟等问题出现的概率。其基本流程如下:

步骤1：根据式（1）初始化一个规模为n的粒子群，设定其为初始粒子群。

式中n为粒子群中粒子的个数；Ub(i)、Lb(i)为每个粒子中第i个个体的上下限值；rand(1)为服从[0,1]均匀分布的随机数。

步骤2：根据式（2）罚函数[6]公式对每个粒子的适应度值进行计算。

式中F(x,M)为罚函数，M为罚因子，为一正常数；Wb(x)为优化问题的目标函数；g(x)为优化问题的不等式约束条件。

步骤3：对每个粒子将其适应度值和其目前的最佳位置pbesti的适应度值进行比较，若较小，则将其作为目前最佳位置。

步骤4：对每个粒子将其适应度值和其全搜索空间的最佳位置gbesti的适应度值作比较，若较小，则将其作为全搜索空间最佳位置。

步骤5：根据式（3）和式（4）分别对粒子的位置和速度进行更新。

其中c1和c2为学习因子一般取2，r1和r2为相互独立的伪随机数，服从[0,1]上的均匀分布，x为压缩系数；ω和Φ为权重系数；fmax、fmin和favg分别为粒子解的最大、最小和平均值。

步骤6：对更新后的粒子群进行交叉重组和变异处理。

步骤7：对变异后的粒子种群进行适应度计算，取得局部最佳位置pbest和目前最佳位置gbest，若gbest满足终止条件则输出解fitness；返回步骤5。

1.2 离散变量的GA-APSO算法

虽然连续型GA-APSO混合算法可以使用在大多数的工程优化问题中。但是还有一些工程的设计变量是离散型的，如在框架结构中使用热轧型钢，这就需要优化后的设计变量的解与型钢库里的型号进行对应。而这种情况是连续型GA-APSO算法所不能实现的，于是在连续性的GA-APSO算法的基础上进行改进得到了离散变量型的GA-APSO算法。

文献[7]对文献[8]的方法针对等步长的离散变量问题进行了改进，即将连续设计变量取为最接近的等步长离散变量，表达式如下：

然后将每一个设计变量同给定的取值进行比较，取其最为接近的变量为该变量的给定离散变量。该方法对于连续等步长的独立的离散变量问题拥有很好的使用性。

但是对于给定的数据库中的离散变量的组合是无规律的，这就需要对优化出来的离散变量进行映射函数处理。由于本文是钢框架，对于其结构的特性，采用主控变量，对于钢框梁而言以强轴惯性矩为主控变量；对以钢框柱来说，将柱截面的截面面积作为主控变量；针对钢框梁和钢框柱分别编写两组映射函数，具体表达式如下：

离散变量的GA-PSO算法的步骤如下：

步骤1：初始化一个规模为pop的粒子群，设定初始位置和初始速度；

步骤2：对每个粒子进行适应度值的计算；

步骤3：对每个粒子将其适应度值和其目前的最佳位置pbesti的适应度值进行比较，若较小，则将其作为目前最佳位置；

步骤4：对每个粒子将其适应度值和其全搜索空间的最佳位置gbesti的适应度值作比较，若较小，则将其作为全搜索空间最佳位置；

步骤5：根据式（3）和式（4）分别对粒子的位置和速度进行更新；

步骤6：对更新后的粒子群随机进行交叉重组和变异处理从而产生新的种群；

步骤7：根据式（10）对变异后的粒子群的进行变量离散和数据库匹配；

步骤8：对匹配后的粒子群的每个粒子进行适应度计算，若满足终止条件则输出解fitness，否则进行步骤5。

离散变量GA-PSO算法的流程图见图1。

将变量离散化的函数用于GA-PSO算法的求解适应度函数值之前，以保证离散后的变量能满足约束条件的要求；这种取值方法不是向上取整,而是将其直接与离散值进行靠拢,更有利于更快地得出问题的解；该方法不存在匹配后不满足约束条件的情况，避免了验算约束条件再匹配的复杂计算循环。

图1 基于离散变量的GA-PSO算法流程图Fig.1 The process of GA-PSO algorithm with discrete variables

2 钢结构优化算例

本章使用离散变量的GA-PSO算法工具箱对两个算例进行优化分析，本算例中所使用的型钢数据库为SAP2000v15中中国规范的GB、JG涉及热轧H型钢共计60种尺寸，并将优化后的结果与基于离散变量的APSO优化算法优化后的用钢量进行对比。

2.1 优化计算数学模型

对于非线性约束优化问题的数学模[9]型可表示为：

式中：f(x)为优化问题的目标函数，在解钢结构优化问题中往往是构件的截面面积、用钢量、总造价等；x为设计变量，一般为结构构件的截面尺寸；gj(x)和hi(x)分别为不等式约束条件和等式约束条件。

根据《钢结构设计规范》(GB 50017-2003)[10]得到钢结构构件的目标函数和约束条件[11]如下：

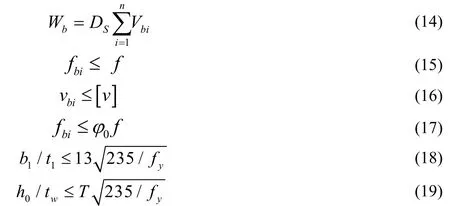
式中Wb钢构件的总重量；DS钢材密度；Vbi钢构件的体积；fbi钢构件i在最不利荷载工况下的计算应力；f相应的强度设计值；vbi钢构件i在最不利荷载工况下的计算挠度；[v]设计挠度限值；φ0构件的整体稳定系数；b1翼缘板外伸宽度；t1翼缘板厚度；h0截面高度；tw腹板厚度；T根据不同情况[3]所取得局部稳定系数。

3 算例1

如图2所示，该算例为5层单榀框架；轴距5 m；层高2.6 m；楼面恒载30 kN/m；梁柱采用Q345B级钢；楼面活载6.25 kN/m；屋面恒载35 kN/m；屋面活载5 kN/m；荷载组合1.2恒+1.4活。模型由SAP2000建模并赋值计算，梁柱的最大内力见表1；SAP和优化工具箱优化后的尺寸见表2。

表1 构件最大内力Table 1 The maximum internal force

表2 优化结果对比Table 2 Contrast after optimization

由表2可知，基于离散变量的GA-APSO优化工具箱求解得到的截面尺寸的应力比比离散变量的APSO算法所得到的稳定应力比要小，这是因为在型钢型号改变的情况下结构自重有所变化而导致的；通过总重量，证明离散变量的GA-APSO优化工具箱的解的截面属性利用的更充分；由图3可知离散变量的GA-APSO工具箱计算出的算例的总用钢量为2.7 t，离散变量的APSO算法计算的总用钢量为4.4 t，节省了1.7 t。由此可得，基于离散变量的GA-APSO优化工具箱优化效率高、适用性强，能满足实际工程中的使用。

图2 一榀框架示意图Fig.2Aschematic framework

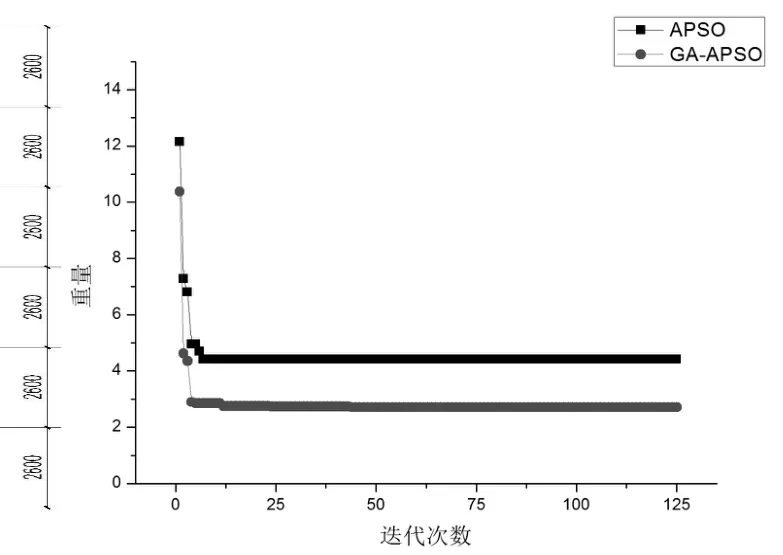
图3 适应度曲线Fig.3 The curves of suitability

4 算例2

本工程为文献[12]中某办公楼算例，地上三层，底层高4.5 m，二层三层均为4 m。工程所在地区基本风压0.55 kN/m2，B类，基本雪压0.25 kN/m2，抗震设防烈度8度（0.20 g），II类。框架平面及横向框架立面示意图如图4和图5所示。

图4 平面示意图Fig.4 The flat schematic plan

图5 立面示意图Fig.5 The schematic elevation plan

表3 构件内力Table 3 Internal forces of components

表4 优化前后结果对比Table 4 Contrast before and after optimization

从表3可以看出：在满足工程约束条件的前提下，GA-APSO算法得到了较为理想的截面选型结果，其中GKL的截面优化率达到18.7%，GKZ为22.2%；并且应力比增大提高了截面的使用率。

从上面两个优化算例的计算结果可得，离散变量下的GA-APSO算法具有一定的实用性，并且优化性能较为优良。

5 结论

（1）本文通过智能算法的特性将遗传算法（GA）中的交叉、变异算子编入加速粒子群算法（APSO）中改进了PSO算法易早熟收敛的缺陷，并加入了主控变量这一概念将种群中的个体得以与截面数据库中的设计变量一一对应，大大增加了工程的实用性。

（2）本文通过两个算例证明，离散变量的GA-APSO算法较APSO算法的优化效率更高，在满足工程约束条件的前提下较大的优化截面尺寸提高截面的使用率。

（3）通过算例的计算结果可得出离散变量的GA-APSO算法，可用于实际工程。

[1]Kiranyaz S,Ince T,Gabbouj M.Multidimensional Particle Swarm Optimization for Machine Learning and Pattern Recognition[M].Berlin:Springer Berlin Heidelberg,2013

[2]Agrawal J,Agrawal S.Acceleration based Particle Swarm Optimization(APSO)for RNA Secondary Structure Prediction//Selvaraj H,Zydek D,Chmaj G.Progress in System Engineering:Proceedings of the Twenty-Third International Conference on System Engineering[M].Switzerland:Springer International Publishing,2015:741-746

[3]Alberdi R,Khandelwal K.Comparison of robustness of metaheuristic algorithms for steel frame optimization[J]. Engineering Structures,2015,102:40-60

[4]黄冀卓,王湛,龚明袖.遗传算法在钢结构截面优化设计中的应用[J].四川建筑科学研究,2005,31(3):26-31

[5]Farkas J,Jármai K.Optimum Design of Steel Structures[M].Berlin:Springer-Verlag,2013:19-23

[6]余胜威.MATLAB优化算法案例分析与应用[M].北京:清华大学出版社,2014:156-157

[7]蔡保佩.基于粒子群算法的刚架结构的优化[D].大连:大连理工大学,2014

[8]陈曦.离散粒子群算法的改进及其应用研究[D].合肥:安徽大学,2014

[9]赖炎连,贺国平.最优化方法[M].北京:清华大学出版社,2008

[10]中华人民共和国建设部,中华人民共和国质量监督检疫总局.钢结构设计规范(GB5O017-2003)[S].北京:中国计划出版社,2003:22-33

[11]王湛,黄冀卓,龚明袖.MATLAB优化工具箱在钢结构截面优化中的应用[J].工业建筑,2002,32(8):72-74

[12]苑辉.钢结构设计计算与实例[M].北京:人民交通出版社,2008

The Optimal Analysis on Steel Structure Based on GA-APSO Algorithm with Discrete Variables

HAO Run-xia,YUAN Shuai*,ZHAO Gen-tian
College of Architecture and Civil Engineering/Inner Mongolia University of Science and Technology,Baotou 014010,China

To overcome the shortcomings of“Premature Convergence"and poor local search ability in Genetic Algo rithm and Particle Swarm Optimization Algorithm,this paper proposed a new heuristic modern hybrid algorithm—G enetic-Accelerating Particle Swarm Optimization Algorithm(GA-APSO)by inserting the cross and mutation operat or of Genetic Algorithm based on Particle Swarm Optimization Algorithm improved speed and position update oper ator functions.The algorithm could expand the scope of the search field to improve convergence speed so that mo re reasonable optimal solution was obtained.Furthermore,GA-APSO algorithm with discrete variables was derive d by inserting the mapping function.It was feasible to automatically select the medium-sized steels in a database b y comparing with the APSO algorithm with discrete variables to take a common framework for an example.

GA-APSO;steel structures;optimization design

TU391;O224

A

1000-2324(2016)06-0900-06

2016-05-12

2016-06-26

国家自然科学基金项目(51268042)

郝润霞(1972-),女,硕士,副教授,研究方向:结构优化理论和设计.E-mail:haorx5300630@163.com

*通讯作者:Author for correspondence.E-mail:yjp415@163.com