基于六面体单元程序计算地基沉降

田志昌,赵波,赵根田

内蒙古科技大学建筑与土木工程学院,内蒙古包头014010

基于六面体单元程序计算地基沉降

田志昌,赵波*,赵根田

内蒙古科技大学建筑与土木工程学院,内蒙古包头014010

本文根据线弹性力学的有限单元法，选用六面体单元，借助Fortran 90具有模块化、封装机制、自定义等编程特性，开发线弹性阶段的六面体单元计算程序，为计算地基沉降提出一种可行、有效的方法。并利用该方法能自行修订所需参数，以达到计算精度要求。最后，通过与ANSYS软件计算模拟地基沉降的结果比较与分析，验证其可靠性和适用性，并对比不同节点六面体单元的精确度。

Fortran 90;六面体单元;地基沉降

地基沉降量的控制是防止产生不均匀沉降而出现裂缝、局部倾斜等工程安全隐患的关键[1]，因此地基沉降的计算和预测成为建筑地基设计的核心问题。目前其计算方法主要分为两种：一种是把分层总和法做为基础的实用计算方法；另一种是以建立材料本构关系为主的有限元等数值方法[2]。而我国在《建筑地基基础设计规范》[3]中，建议使用对分层总和法修订后的规范法。虽然该方法的适用性较好，但即便是同一规范中，由于Ψs，压缩层厚度确定方法的不同[4,5]，都会导致不同的计算值。且规范法以一维变形的假定也影响了计算精度。因为土层的几何构造和受力情况以三维性为主，其一维压缩只是一种特殊情况，如在内蒙古包头地区高层建筑厚筏板基础沉降计算中，规范法计算结果与实测沉降值存在较大误差，个别工程竟高达允许误差的5倍，故该方法并不具有参考价值[6]。

数值理论方法较为完善，可以考虑非线性、弹塑性等，伴随着计算机技术的发展，产生了许多具备计算地基沉降的有限元软件，如AbAQUS，ANSYS但土性参数的确定比较复杂和困难，且选取参数的种类也不同[7]。因此，我国许多的软件，如YJK，GS等，都还没有嵌入三维实体单元计算模块。所以，本文试图先在线弹性阶段结合六面体等参数单元理论和Fortran 90[8]编程语言，开发应用程序来计算地基沉降的方法。为进一步探索非线性阶段的编程尊定基础。首先，三维六面体单元具有块体形状的特性，适合模拟岩土这种固体，故用它来计算地基沉降和承载力分析具有一定的优越性。再次，这种小型计算程序可以使具备Fortran 90编程知识的使用者，针对地基实际情况，自行在程序中添加或减少影响地基沉降的控制参数和条件，来达到所需的准确度。

1 六面体单元程序的理论基础

1.1 等参数单元

母单元和子单元是所有等参数单元的两种单元形式。在母单元内主要进行计算工作，这是由于它具备计算精度高和适用性好的特点。而子单元充分反应了来自结构的实际特征。这两种单元的相互映射则是通过形函数进行坐标变换来达到的，因此就存在着存在着两种不同的坐标系，即全局坐标（X，Y，Z）和局部坐标(ξ，η，ζ)。子单元的直角坐标系始终是全局坐标；而局部坐标不仅扮演着母单元的直角坐标系，也扮演着子单元的曲线坐标系两种角色。并且曲线坐标系只适用于单个独立的子单元，而直角坐标被整个结构中的所有子单元中共同使用。

所以等参数单元对于曲线边界和曲面边界适应性更强，模拟结构形状更加准确，也因其位移模式阶数较高而更好地反映结构中复杂的应力分布，并且还可以灵活的增减结点来构造各种过度单元。

1.2 单元形态的布置

由于等参数单元进行了坐标变换，所以其单元内应变的变化规律，不仅取决于形函数的阶次，并且还与单元形状及各边节点位置相关，因此需要确定单元形态。同时单元节点编号，相应的形函数位置和顺序须与其规定的单元形态（母单元）相符合，否则会导致雅克比矩阵行列式值为负（单元形态出现内凹现象），进而使计算结果错误或程序不能运行。

六面体等参数单元包括线性和二次两种单元，其单元形态布置分别采用图1和图2的单元（母单元）形态，全局坐标系采用右手坐标系，Z轴向上。

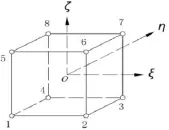
图1 8节点空间等参元Fig.1 The isoparametric elements in 8 nodes

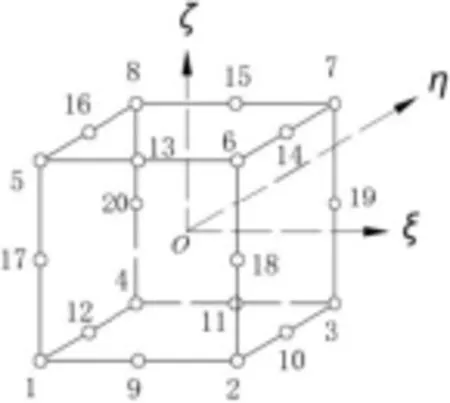
图2 20节点空间等参元Fig.2 The isoparametric elements in 20 nodes

1.3 本构矩阵

弹性D矩阵也称本构矩阵，对于不同的材料性质，如极端各向异性体、正交各向异性体等，都可化为6*6弹性常数矩阵，实质是材料不同其中包含的独立弹性常数不同。由于只考虑线弹性阶段，因此它的本构关系符合广义的胡克定律，即弹性体材料的弹性模量E和μ泊松比决定了它的独立弹性常数，如式(1)。

1.4 应变矩阵和雅克比矩阵

通过把单元位移函数式代入到空间应变问题的公式中，即可得到：

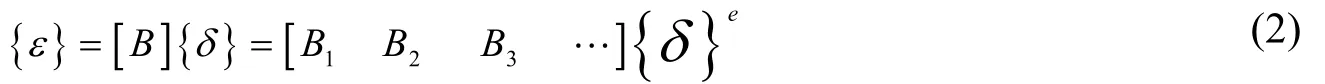
式中B就为应变矩阵。根据微分法则并对其进行集合，得到：

式中i为节点数，(x，y，z)为全局坐标，形函数Ni(ζ，η，ξ)则是用局部坐标表达的，

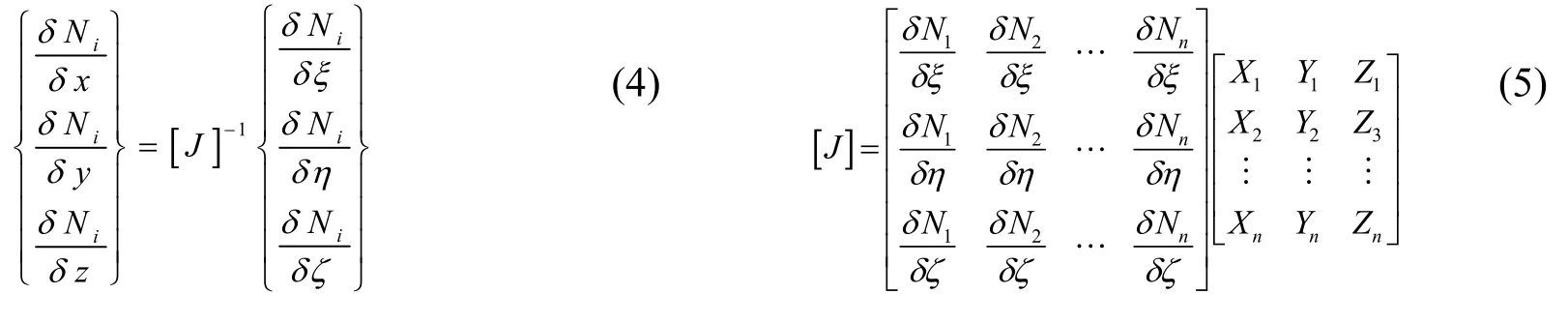
通过公式(4)和(5)的分解与回代，可得到应变B矩阵。从积分学可知，雅克比矩阵｜J｜＞0是两个坐标之间一一变换的充要条件，所以等参变换也必须服从此条件。如果｜J｜=0，则[J]-1不存在，产生导数和微元转换也就不存在，变换不成立。其中雅克比率的概念就是是给定单元偏离理想单元（正常单元）的一个度量，其取值范围是-1.0到1.0。1.0代表理想单元形状。测量方法本质就是通过映射的方式把局部坐标下的理想单元形状转化为全局坐标下的实际形状。

1.5 单元刚度与数值积分

整个结构矩阵计算中的一个核心环节就是单元刚度矩阵的形成。单元刚度矩阵在很大程度上决定着计算结果的精度，它随着单元几何形状、节点数目及节点自由度选用的不同而发生变化。单元刚度矩阵中的弹性矩阵则取决于材料的物性参数。由此可见，只要单元的几何形状及其材料物理特性确定，单元的刚度矩阵就可确定。

式中ξi，ηj，ζk为积分点，Wi，Wj，Wk为权系数，nip为积分次数。

数值积分有两类积分方法，包括所取积分点是等间距和不等间距的。此处采用积分点不等间距的高斯积分法，因为它可以在积分点数目确定的情况下通过选择位置更加合理的积分点来减少积分点的索取数量并达到更高的精度，从而节省机器时间和便于程序的实现。虽然各维数上的积分点数目由各个自变量在被积函数中可能出现的最高次数分别决定但为使用方便，常常统一为最高值。因此，对于线性六面体单元采用2*2*2规则计算单元刚度矩阵，二次单元则采用3*3*3规则来计算。

1.6 结构刚度矩阵组装、存贮和分解

结构刚度矩阵是由单元刚度矩阵组装而成，包含了每个单元对结构产生的贡献作用，这种贡献作用的叠加则是通过单元定位向量来完成的。单元定位向量不仅使每个单元的各个未知量在结构未知量中确定相应的位置还考虑了每个单元的边界条件，很方便地解决了程序编写时计算机自动化中所需的信息。对于结构刚度矩阵的存贮，采用节省存贮单元的一维变带宽存贮，这种存贮方法不仅可以提高计算效率还对减小舍入误差有着明显的效果。其存贮方式有按行存贮和按列存贮两种[9]，存贮序号分别按公式（8）和（9）计算。

上式中字母I，J分别代表元素的行列号，数组KD存放结构刚度矩阵中的主对角线上的元素。

本程序中结构刚度矩阵主对角元素选用按行存贮。因为分解结构刚度矩阵时采用消元分解法，而消元分解法求解时是按行进行肖元的，比按列存贮更有效。最后通过结构静力学有限元方程（10）即可解出节点位移量。

其中{F}为节点载荷向量；[K]为结构刚度矩阵；{d}为节点位移量。

图3为主程序的结构图，揭示了程序编写的方案和各个子程的作用,并且给出了计算线性六面体单元刚度矩阵的示例程序。

图3 主程序流程图Fig.3 The process of main program

计算线性六面体单元刚度矩阵程序:

2 计算模拟地基沉降

2.1 六面体单元程序计算地基沉降

本计算程序所适用的单元材料属性由其本构矩阵D来确定，采用有限元法中的小片检验的原理[10]来检查、验证。模拟地基的模型建立和有限单元的划分借助ANSYS软件。为此采用简化实用的地基模型进行沉降计算，其模型分析步骤如下：

(1)地基表面受6种不同的工况荷载，分别为：120 KN/m2、130 KN/m2、150 KN/m2、170 KN/m2、180 KN/m2、200 KN/m2；(2)不计地基重力作用；(3)边界条件：①所有垂直边界水平位移为零；②底部网格所有节点垂直、水平位移为零；③所有垂直边界不排水。(4)杂填土下为基岩；(5)表1提供模拟所需计算参数；(6)图4为地基沉降计算简图。

图4 地基沉降计算简图Fig.4 the diagram calculating foundation settlement

表1 地基模拟的计算参数Table 1 Parameters of foundation simulation

依据表1和模拟分析步骤的内容，表2和表3分别表示模拟地基在6种不同工况荷载下，利用六面体单元程序中不同节点单元计算的最大沉降值。

2.2 ANSYS计算地基沉降

ANSYS软件因具有多场耦合分析功能，不仅能使岩土力学性能的模拟更加准确，还可以考虑非线性的本构关系及分期施工过程，使实际情况在模拟中得到较好地反映。其中Drucker-Prager屈服准则可为岩土介质的模拟计算提供精确的结果。采用DP本构模型,采用SOLID45(线性六面体单元)和SOLID95(二次六面体单元)两种单元形式进行划分，计算2.1中模拟地基在6种不同荷载下的沉降值，计算结果为表4。

表4 ANSYS计算地基沉降值Table 4 The value of foundation settlement calculating byANSYS

3 结论

(1)本文用ANSYS、六面体单元程序对模拟地基的沉降进行了计算。从图5和图6中得出，相对于ANSYS计算模拟地基的沉降值，使用六面体单元程序的线性六面体单元计算模拟地基的沉降值与ANSYS计算值之间的误差约为3%。而使用其中的二次六面体单元计算模拟地基的沉降值与ANSYS计算值之间的误差约2%。说明应用程序单元形态的布置与节点形函数的布置一致，程序编制正确，调试、运行流畅，以及使用的理论公式和数学方法基本正确。同时也说明六面体单元程序中使用二次单元计算精度要高于使用线性单元，其单元适应能力更强，实际运用中能用其较少或适量的单元划分得到精确的计算结果。

图5 ANSYS和线性六面体单元程序计算结果对比图Fig.5 The comparison betweenANSYS and the program of linear hexahedral element

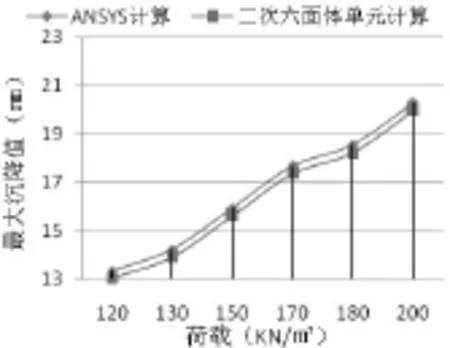
(2)通过与ANSYS计算结果的比较，六面体单元应用程序的整体性、融合性、各个子程序之间的协调性、计算结果的可靠性和适用性良好，不仅为程序非线性阶段的编制奠定了基础，也可视为计算地基沉降的一种方法，并与其它方法相结合来有效地防范和应对施工沉降中出现的一些特殊情况，也可为设计、施工人员或科研工作者解决或预测地基沉降提供有效的参考和对比。

[1]周德泉,杨志华,邓超.复合地基沉降分析与计算方法研究[J].公路与汽运,2015,1(170):85-88

[2]杨光华.地基沉降计算的新方法[J].岩石力学与工程学报,2008,27(4):679-686

[3]中华人民共和国建设部.GB50007-2002建筑地基基础设计规范[S].北京:中国建筑工业出版社,2002

[4]张钦喜,刘鸿哲,樊绍峰.地基沉降计算方法的研究与改进[J].北京工业大学学报,2009(1):78-83

[5]刘全林,魏焕卫.地基沉降计算中压缩层厚度确定方法的比较[J].岩土工程技术,2001(4):208-209

[6]张宁.类比法预测包头市民营经济发展中心公寓基础沉降[D].包头:内蒙古科技大学,2013

[7]曹强.基于施工沉降观测值预测深层回填土地基最终沉降[D].包头:内蒙古科技大学报,2013

[8]颜慧军,王友海.程序设计语言FORTRAN90研究与应用[J].哈尔滨建筑大学学报,2000,33(2):105-109

[9]赵超燮.结构矩阵分析原理[M].北京:人民教育出版社,1982:148-149

[10]朱伯芳.有限单元法原理与应用[M].第三版.北京:中国水利水电出版社,2009:154-157

Foundation Settlement Calculated by the Program of Hexahedral Element

TIAN Zhi-chang,ZHAO Bo*,ZHAO Gen-tian
College of Architecture and Civil Engineering/Inner Mongolia University of Science and Technology,Baotou 014010,China

According to the linear elastic mechanics for finite element,this paper chose the most common hexahedral element to resort to Fortran 90 with the characteristics of modularization,encapsulation mechanism and custom to develop the program of hexahedral element in the linear elastic stage so as to propose a feasible and effective method to calculate the foundation settlement.This method was used to revise the required parameters in order to meet the precision of the calculation.Finally,the results between this method and ANSYS simulation were compared and analyzed to verify the reliability and applicability and contrast the accuracy of hexahedral element in different nodes.

Fortran 90;hexahedral element;foundation settlement

U446.1

A

1000-2324(2016)06-0841-05

2016-06-28

2016-08-30

国家自然科学基金(51268042)

田志昌(1962-),男,内蒙古包头人,博士,教授,主要从事有限元软件开发和防灾减灾.E-mail:1435227030@qq.com

*通讯作者:Author for correspondence.E-mail:308012774@qq.com