均值不等式和割、切线法在水力学分析中的应用

程铁杰,周婷

1.安徽农业大学工学院,安徽合肥230036

2.合肥工业大学土木与水利工程学院,安徽合肥230009

均值不等式和割、切线法在水力学分析中的应用

程铁杰1,2,周婷1*

1.安徽农业大学工学院,安徽合肥230036

2.合肥工业大学土木与水利工程学院,安徽合肥230009

文章提出了两种数学方法在水力学分析与计算中的应用：1)均值不等式在推求矩形断面明渠临界水深计算上的应用；2)割线法、Newton切线法以及两者相结合的方法在求解水力学方程上的应用。从理论上阐述了两种数学方法在水力学分析中应用的可行性，并通过实际算例进行验证。不仅为水力学课程教学与解题提供了新的思路，也为实际工程计算中的有关问题提供了可行简便解决途径。

均值不等式;割线法;Newton切线法;水力分析

《水力学》是水利、土木、市政等专业的重要专业基础课之一，其内容涉及大量的理论和经验公式，尤其是高次方程的求根和非线性方程组的求解等问题，给课程教学和工程计算带来了繁杂的计算量和难度。教材中提及的方法如图解法、试算法以及不动点迭代法在有限的计算次数内往往难以满足实际中需要的精度[1]，容易造成误差累积，导致结果偏差过大；另一方面，若提高试算迭代的次数则会大大增加计算量，往往会影响设计效率，在实际工程中实践起来并不现实。因此，合理运用相关数学原理实现公式快速有效求解，对于理解水力学原理、提高求解效率和精度具有良好的理论和实际意义。对于方程（组）的求解这一中心问题，即f(x)=0，不同教材中都阐述过许多方法与技巧；在实际应用当中，随着f:的不断扩充，最具启发性的仍是f:R→R；极值问题和上下确界的确定很多也可以化归到f´(x)=0的问题上来。近年来，随着计算机和信息技术水平不断发展，求解的速度和精确度也在不断的提升，但在实际问题的分析中仍然面临以下两个方面的困境：一方面，求根的方法代价太大，有时甚至无法求解，而且“快速”算法并不总能找到方程的根；另一方面，一些数学条件的约束使得计算机验证起来并不容易。本文分别介绍了均值不等式方法和割线法、Newton切线法以及二者相结合的方法在水力分析与计算上的应用方式，在保证精度的同时降低了计算量，提高了计算效率。

1 数学理论

1.1 均值不等式

算数—几何均值不等式的定义如下：若x1，x2，…，xnÎR+，那么An≥Gn。

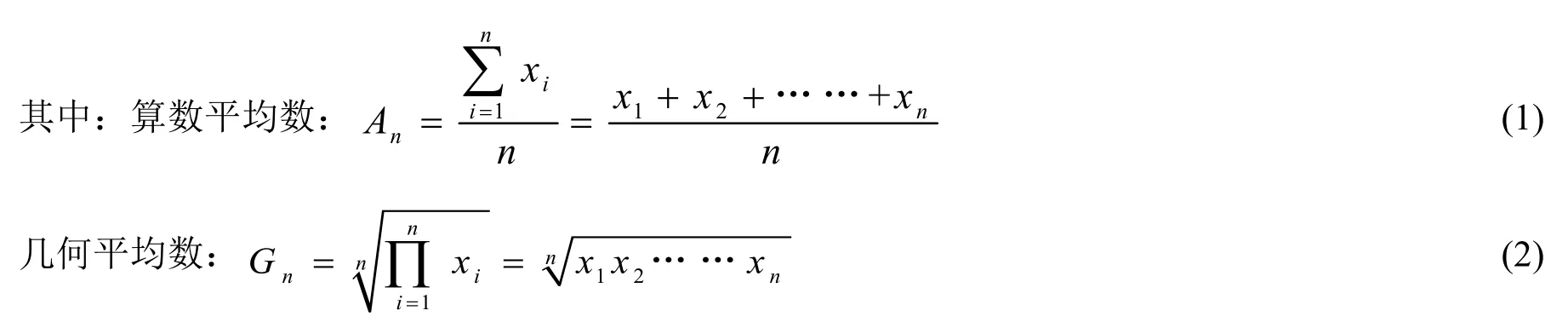
即这些正实数的算术平均数大于等于它们的几何平均数，等号成立当且仅当x1=x2=…=xn[2]。均值不等式的广泛应用已经得到了人们的重视[3]，本文对均值不等式的应用仅涉及n=3时的情形。

1.2 割线法与Newton切线法

割线法与Newton切线法是非线性方程求根的两种方法[4]，其概念如下：

设f:[a,b]→R，则f(x)=0是否在[a,b]上有根可以利用介值定理来判定（本文仅讨论单根情形），设fʺ(x)>0，f(a)>0，f(b)<0，则$x0Î[a,b]使得f(x0)=0。

割线法：用过(a，f(a))，(b，f(b))的连线代替f(x)。则割线方程为：。

Newton切线法：用f在a点（或b点）的切线求根。

即：用y=f(a)+f´(a)(x-a)代替f(x)，令y=0可以得到。迭代公式为：，则an单调递减地收敛到x0，并且f´(x0)≠0。

由于水力计算中涉及到的高次方程（组）较多，其方程形式多变复杂。试算法和不动点迭代法[5]大多均为1阶收敛，计算过程中存在过于依赖初始值的弊端，而且实际应用中都忽略了对不动点的存在唯一性做验证这一过程，致使最终不能较为精确地求得方程的根。而割线法和Newton切线法比较容易应用于水力计算中，割线法是1阶收敛，Newton切线法是2阶收敛，采用近似程度更高的二阶Taylor展开式可以使收敛速度进一步加快[6]。因此在计算中如需求得高精度的结果，可考虑使用Newton切线法来求根，能够节省迭代次数。

但Newton切线法存在一个不足之处，对于复杂方程f´(x)不易求得，那么考虑和割线法相结合的方式对Newton切线法迭代公式做一些改动，用代替f´(an)进行迭代直到满足结果需要的精度，这种方法在数值分析中称之为弦截法[7]，即割、切线相结合的方法。

2 方法应用

2.1 均值不等式在矩形明渠水力计算中的应用

在明渠恒定非均匀流计算中，选取渠底为参考基准面，计算得到过水断面单位重量液体所具有的能量称为断面比能，其表达式如下[8]：

式中：Es—断面比能（m）；h—水深（m）；θ—明渠底面对水平面的倾角；α—动能修正系数（通常取α≈1.0）；v—断面平均流速（m/s）；Q—流量（m3/s）；A—过水断面面积（m2）

相应于断面单位能量最小值的水深称为临界水深，用hK表示；这里利用均值不等式来推求矩形断面的断面比能和临界水深。

当等号成立时，断面单位能量取到最小值，这时的h就是对应于断面单位能量最小值的水深，也就是临界水深，此时h=hK。

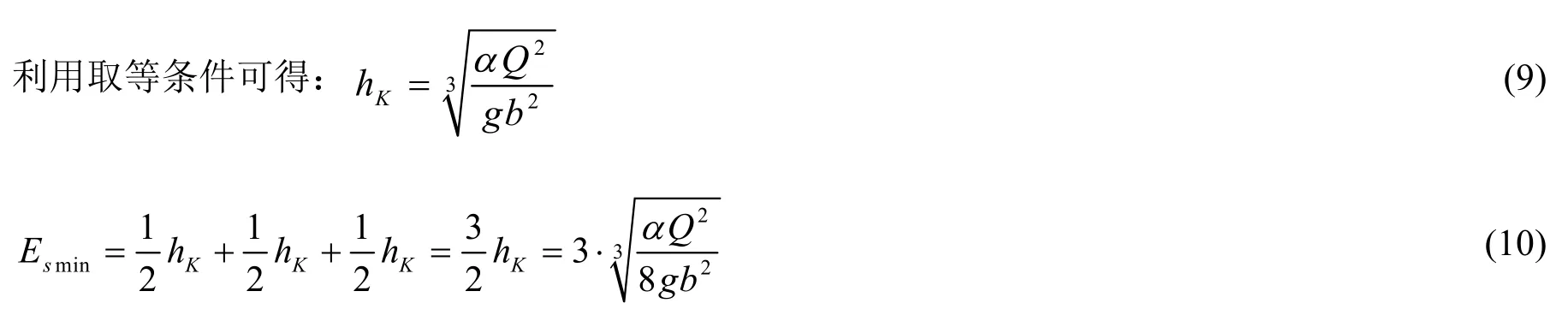
可见，利用均值不等式方法推导矩形断面的断面比能和临界水深更为简单易行，且方便记忆，避免了诸多复杂的计算过程。

2.2 割线法与Newton切线法在梯形明渠水力计算中的应用

对于梯形断面明渠恒定非均匀流临界水深的计算，过水断面面积A与水深间的关系较为复杂，临界水深hK的直接解不易求得；教科书中大多采用试算法和图解法求解，计算繁琐，结果精确度也欠佳；传统的二分法迭代[9]收敛速度较慢，当精度要求较高时，迭代次数会大大增加；而采用割线法，Newton切线法以及割、切线相结合的方法则能求得较为精确的结果。

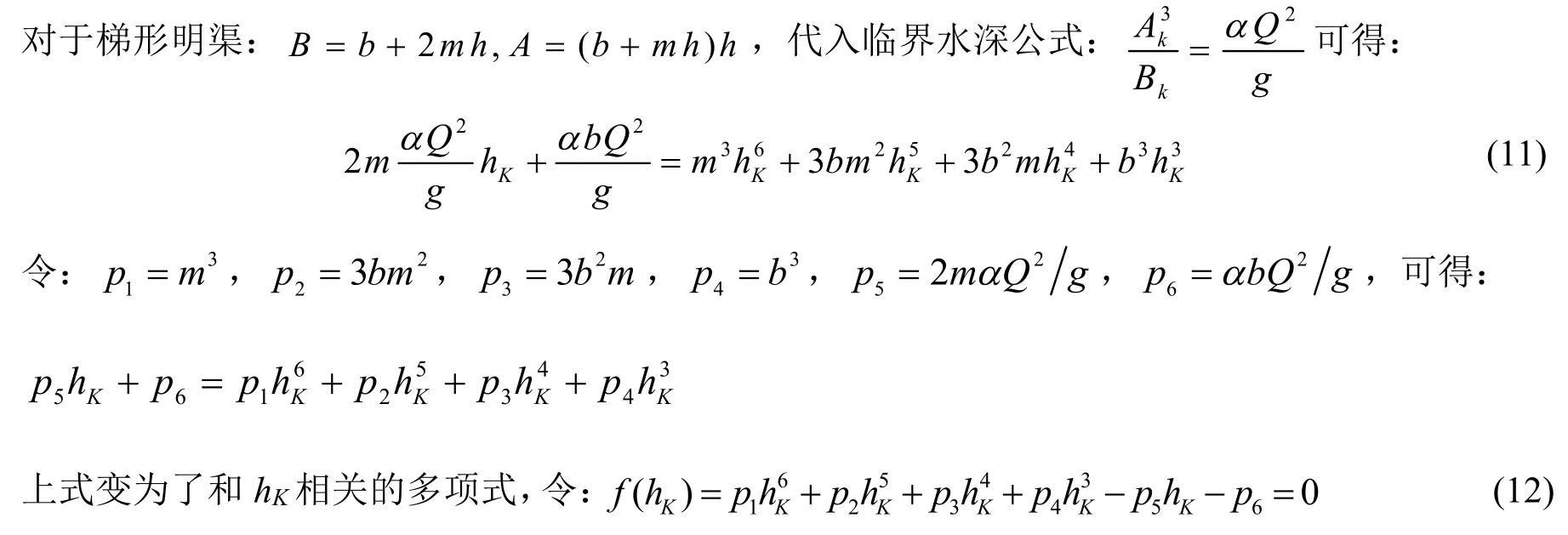
可见，梯形断面临界水深问题已经转化为多项式方程的求根问题；由于在实际问题中pi(i=1,2,…,6)，hK均大于零，因此fʺ(hK)>0，函数曲线在[0,+∞)上为凸函数（下凸）；且当hK→0时，f(hK)<0；当hK→+∞时，f(hK)>0；所以在区间[0,+∞)内只有一个正实根[10]。故而在区间[0,+∞)之中可以取得区间[a,b]，使得f(a)<0，f(b)>0，根hK在区间[a,b]中。

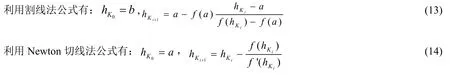
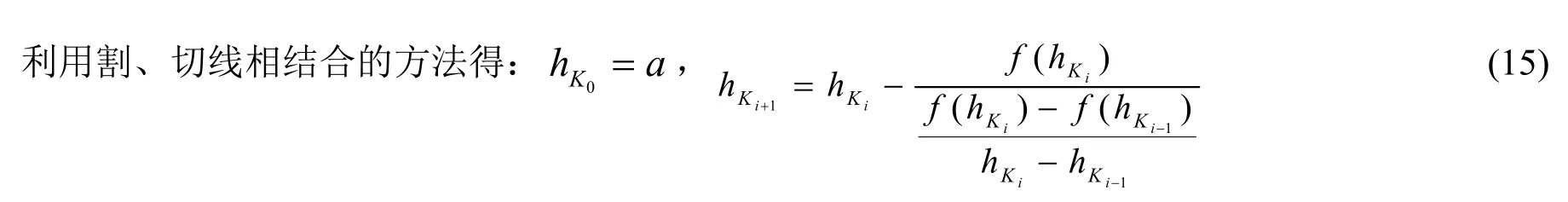
在实际问题中应根据具体问题对计算式进行化归后选用适当的方法迭代，在计算简捷的前提下迭代至需要的精度。

3 算例

3.1 均值不等式方法实际算例

一矩形断面明渠，流量Q=30 m3/s，底宽b=8 m，求渠道中最小断面比能及临界水深。

分析：本例常见于灌溉渠道设计中；关于矩形明渠恒定非均匀流最小断面比能和临界水深的计算，在水力学教材[11]中的计算方法是根据式（5），对水深h取导数，并令其等于零，推出临界水深应满足的条件，这种方法在求导时计算繁杂，最小断面比能还需进一步通过临界水深来计算；王功[12]根据断面比能曲线的特点，取两个相近数值h1和h2（h1>h2）带入式（5）计算出相应的ES1和ES2，通过比较ES1和ES2的大小关系，进行临界水深的推求，计算量仍然较大；陈文英[13]根据伯诺里方程导出了明渠恒定非均匀流的水面曲线微分方程，把断面比能的变化率同临界水深的变化率联系起来进行临界水深的计算，该方法在实际计算中依然不能对临界水深和最小断面比能进行快速求解。均值不等式通过对计算式拆分和放缩，避免了复杂的计算量，通过对取等条件的分析可以快速得出临界水深的取值。

所以计算结果正确，即最小断面比能为1.692 m。临界水深为1.128 m。

3.2 割线法与Newton切线法实际算例

一分叉管道连接水池A，B，C（见图1）。设1，2，3段管道的直径及长度分别为：d1为60 cm，l1为900 m；d2为45 cm，l2为300 m；d3为40 cm，l3为1200 m；管道为新钢管，A，B，C水池的水面高程为：▽A为30 m，▽B为18 m，▽C为0 m。求通过各管道的流量Q1，Q2，Q3。

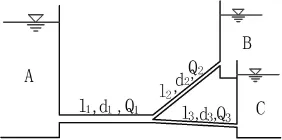
图1 分叉管道水池示意图Fig.1 Sketch of penstock manifold pool

分析：水力学教材对于并联管道的水力计算中解方程的方法仍为试算法和图解法[14]，仇宝云等[15]利用拉格朗日乘数法从理论上阐述了以总水力损失最小为目标，确定分流点从每条管道上的分流量；王萍等[16]利用Excel函数编写程序进行对污水管道的水力计算，计算过程中需要假设和判断的过程；陈继泉[17]通过对管道系统和某些局部管网或节点状态进行适当简化得出长输水管道系统水力计算的简化模型。割线法和Newton切线法在管道水力计算中可以定量分析管道输水，同时避免试算法和图解法的误差。

解：查表可得新钢管粗糙系数n为0.012。

由实际情况可知Q1>0，Q2>0，Q3>0；由式（28）、（29）可知Q1<0.769；即：Q1的取值范围是：(0,0.769)，这时方程组求解的问题转化为方程求根的问题，由式（31）可知：f(0)<0，f(0.769)>0，所以存在Q10在区间(0,0.769)中使得：f(Q10)=0。下面分别用Newton切线法和割、切线相结合的方法分别来求解。

用Newton切线法求解构造迭代公式如下：

由于定义域为（0,0.769），取a0=0.5迭代得：a1=0.65194，a2=0.64350，a3=0.64241，a4=0.64240，a5=0.64240。

停止迭代；即：当Q1=0.64240时f(Q1)=0，Q1=064240 m3/s。

用割、切线相结合的方法求解构造迭代公式如下：

取a0=0.4，a1=0.5迭代得：a2=0.67327，a3=0.63707，a4=0.64216，a5=0.64241，a6=0.64240。

停止迭代；即：当Q1=0.64240时f(Q1)=0，Q1=0.64240 m3/s。

可见两种方法殊途同归；将Q1=0.6424 m3/s代入（28）得：Q2=0.3394 m3/s，代入（29）得：Q3=0.3030 m3/s。进一步验算结果得：Q2+Q3=0.3394+0.3030=0.6424=Q1

可知所求结果计算正确。故而各管流量均求出，Q1为0.6424 m3/s，Q2为0.3394 m3/s，Q3为0.3030 m3/s；本例得解。

4 结论

本文以明渠恒定非均匀流中矩形断面和梯形断面的水力计算为切入点，提出了均值不等式和切线、割线法在水力学分析与计算上的应用，不仅从物理角度解释了水力学公式原理，同时降低了计算复杂程度，提高了计算精度和效率。本文所选用的方法可用于水力学教学、水利工程设计计算中，同时这些原理还可以推广至更高维计算以及其他类似工程领域当中，以解决更多工程计算相关问题，具有较强的实用性和可行性。

[1]王仲发,王乐水,张洪存,等.水工建筑物设计中几个常见水力学问题的迭代解法[J].山东农业大学学报(自然科学版),2003,34(2):256-258

[2]匡继昌.常用不等式[M].第3版.济南:山东科学技术出版社,2004

[3]吴善和,石焕南.平均值不等式的推广及应用[J].贵州教育学院学报,2003,14(2):14-16

[4]阿黑波夫,萨多夫尼奇,丘巴里阔夫.数学分析讲义[M].第3版.北京:高等教育出版社,2006

[5]邱秀云,张鸣.迭代法在水力学计算中的应用[J].科技信息,2008(27):281

[6]王家杰,孙娟.牛顿切线法的一种改进及其应用[J].八一农学院学报,1994,17(4):50-53

[7]李庆杨,王能超,易大义.数值分析[M].第4版.北京[海德堡]:清华大学出版社,施普林格出版社,2001

[8]吴持恭.水力学:上册[M].第4版.北京:高等教育出版社,2008

[9]刘为民.二分法在梯形明渠均匀流水力学计算中的应用[J].新疆水利,2000(6):31-34

[10]齐清兰,张力霆,张振军.复杂水力计算中的高次方程问题[J].数学的实践与认识,2006,36(9):163-165

[11]李家星,赵振兴.水力学:上册[M].第2版.南京:河海大学出版社,2001:313-314

[12]王功.临界水深计算方法的研究[J].水资源与水工程学报,2011,22(2):168-170

[13]陈文英.论述明渠非均匀流的系统性[J].华东交通大学学报,1985(2):121-124

[14]李大美,杨小亭.水力学[M].武昌:武汉大学出版社,2004

[15]仇宝云,刘超.并联输水管道最优流量分配及其应用[J].水利学报,1994(6):50-56

[16]王萍,宋晓明.利用EXCEL进行污水管道水力计算[J].环境技术,2003(6):29-31

[17]陈继泉.长输水管道水力计算简化模型[J].水利科技,2001(4):55-156

Applications of Value Inequality and Secant&Tangent Methods in HydraulicsAnalysis

CHENG Tie-jie1,2,ZHOU Ting1*
1.School of Engineering/Anhui Agricultural University,Hefei 230036,China
2.School of Civil Engineering/Hefei University of Technology,Hefei 230009,China

The application of two mathematical methods in hydraulics analysis and calculation is presented in this paper:1)Average Inequality method in the critical depth calculation of rectangular open;2)Secant method,Newton tangent method and their combination in solving hydrodynamic equations.The feasibility of applying two kinds of mathematical methods in hydraulics analysis is expounded theoretically and verified by practical example.The proposed methods provide not only new paths for hydraulics teaching and problem-solving,but also offer practical and simple ways for engineering calculation.

Average value inequality;secant method;Newton tangent method;hydraulics analysis

P333.9

A

1000-2324(2016)06-0835-06

2015-07-22

2016-01-05

程铁杰(1992-),男,硕士研究生,主要从事工程水力学研究.E-mail:ahauchengtj@sina.com

*通讯作者:Author for correspondence.E-mail:zhouting@ahau.edu.cn