场站转场条件下备件携行品种研究
2016-02-08崔国伟王正张登滨李跃井
崔国伟,王正,张登滨,李跃井
(海军航空工程学院青岛校区,山东青岛266041)
场站转场条件下备件携行品种研究
崔国伟,王正,张登滨,李跃井
(海军航空工程学院青岛校区,山东青岛266041)
场站转场过程中备件是否需要携行,携行哪些品种。将问题转化为0-1规划来解决,从而判断是否需要携行。对信息不充足的备件进行分析,排除不需要携行的备件,通过分析备件的寿命分布规律判断备件是否携行。
备件;品种;寿命分布;携行
0 前言
场站转场需要携行一定种类、数量的器材备件,来满足保障的需求。携带的备件品种、数量不足会影响任务的完成,携带过多则会造成资源浪费。因此研究场站转场过程中器材备件携行品种、数量对完成保障任务具有重要意义。场站转场携行的器材备件,根据其消耗和发生故障的信息,可以划分为信息充足的备件和无充足信息的备件。对于不同的备件应当采用不同的方法来确定其是否需要携行。
1 信息充足的备件确定
1.1 判断模型的建立
备件如果有充足的信息,可以从概率的角度来判断其是否需要携行。如果转场的设备数量为x台,备件发生故障的概率为p,x台设备上的备件可以看作是独立重复的实验,那么携行与否的问题就可以转化为成败型的实验来解决,很明显这个问题可以转化为二项分布来解决。也就是将器材备件品种的携行问题归结为0-1规划问题,携行就是1,否则就是0。二项分布的表达式为式(1)。
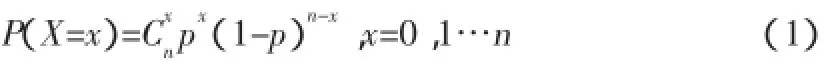
那么备件发生故障的次数小于某个值r的累积分布函数为式(2)。
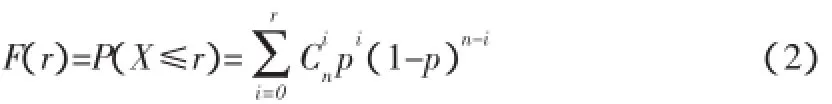
根据式(2)计算结果,当F>0.05时,则该备件需要携行,反之不需要携行。
1.2 应用分析
以转场任务期间有充足信息的a备件为例分析,按照时间顺序将转场批次与a备件消耗数量情况列为表1。发生故障的a备件有17个,11个批次中设备无故障的a备件22个,因此a备件每个批次平均发生故障的概率是p=〔17/(17+22)〕/11=0.04。若11个批次的总的工作时间是858.1 h,则a备件平均每100 h发生故障的概率是p=〔17/(17+22)〕/858.1h=5.1276×10-4/h。

表1 a备件消耗数量
在任务期间每间100 h,a备件发生故障的概率是5.1276× 10-2/100 h。x台设备是独立同分布的整体,也就是x台设备上的a备件发生故障的概率互不影响,将a备件的发生故障的概率代入二项分布式(1)中,当x=0时,也就是不发生故障时的概率(1-p)n,结果为0.9,所以其发生故障的概率p=1-(1-p)n,是0.1,也就是a备件每100 h工作时间内,其发生故障的概率为0.1,大于置信水平0.05,因此需要携行。从实际情况来看,该备件也需要携行。因此,使用二项分布模型判断的结果符合实际情况。
2 无充足信息的备件
2.1 判断模型的建立
携带的备件通常都是成品件,因此在确定携行的品种时以成品件的品种数量为基础,排除不需要携带的品种,从而确定需要携带的品种。需要排除的备件主要分为3类:一是大型、易损坏无法携行的备件;二是野外环境条件下无法进行更换、校准的备件;三是任务期间发生故障概率很小的备件。对于前2种备件结合任务的实际情况能够确定,任务期间不予携行。因此,本文着重讨论第三种,任务期间发生故障概率很小的备件。
对于没有充足信息的备件,都是寿命比较长,发生故障概率很小的备件,使用拟合的方法,没有足够的数据信息判定是否需要携行。这样的备件通常不需要携行。但是,对于没有了历史故障信息又很关键的备件,如果不携行,一旦发生故障,设备就不能正常工作,对于这样的备件是否携行需要慎重考虑。为了解决问题,本文从备件寿命的角度出发来考虑是否需要携行。
从收集到的信息中对于这样的器材,可以得到的数据就是其无故障工作的时间,因此可以对其无故障工作时间进行估计,将估计值和工作时间相比较,如果估计值小于工作时间,就需要携行该备件。依据参考文献[3,4]中无故障的可靠性分析来解决,可以计算其可靠度在95%置信度下的最优置信下限和可靠寿命在95%置信度下的最优置信下限,然后结合实际任务情况来判断是否需要携行。为了简化问题的处理把这个问题当作定时截尾试验来处理。根据经验,备件的寿命分布规律主要是正态分布、指数分布或威布尔分布这几种分布类型,依据不同分布类型作出无故障工作时间估计。
(1)指数分布估计。当备件寿命符合指数分布的时候,对n个备件进行定时截尾试验,在无故障情形下,置信度为1-α,平均寿命θ的最优置信下限见式(3),可靠度R(t)的置信水平1-α下的最优置信下限为式(4),可靠寿命为式(5)。
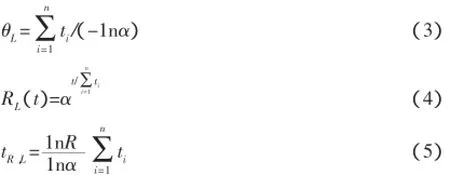
(2)正态分布估计。可靠度在置信水平下的最优置信下限见式(6)。

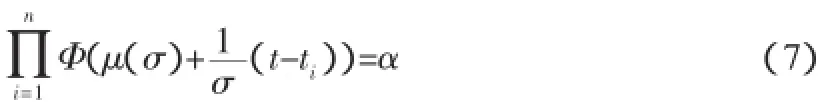
设-∞<μ<∞,σ1<σ<σ2,可靠度R(t)在置信度1-α下的最优置信下限为(8)式。
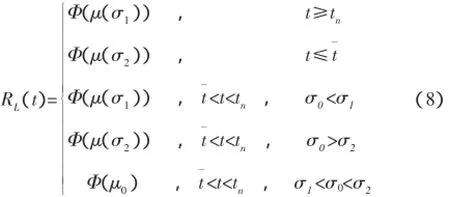
数值方法求解(8)式的解,即得μ(σ2)或者μ(σ2);(μ0,σ0)是(9)式方程组的解。
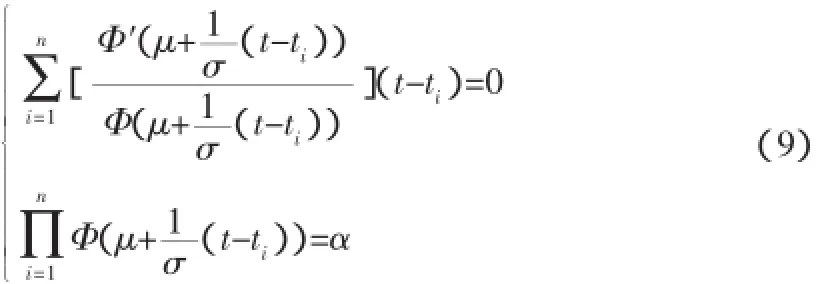
可靠寿命在置信水平下的最优置信下限,设-∞<μ<∞,σ1<σ<σ2,,在无故障数据情形下可靠寿命tR的置信下限为(10)式。

式中μR指标准正态分布的R分位数;p为n个产品中截尾时间等于tn的产品个数;μ*,σ*是式(11)和式(12)2个方程组的解。
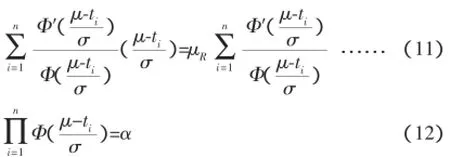
式中μ1(或μ2)是上式的根,当σ=σ1时,由式可求得μ=μ1;当σ= σ2时有式可求得μ=μ2。
(3)威布尔分布估计。备件寿命符合威布尔分布的时候,对n个备件进行定时截尾试验,根据参考文献[3-4],在无故障的情形下,置信度为1-α时平均寿命θ的最优置信下限按照指数分布处理为式(13),可靠寿命为式(14)。
n


2.2 应用分析
以备件的工作时间(小时)为例分析,工作时间依次为72.9 h,102.4 h,57.98 h,89.58 h,84.23 h,73.86 h,99.71 h,42.81 h,54.41 h,103.41 h,76.88 h。
(1)指数分布。对于指数分布的备件,失效率(故障率)恒定,则失效率为λ=1/θ=1/Σt=0.0014,其可靠寿命tR=(1/λ)ln(1/R),取R=0.95,则tR=(1/0.0014)0.0531=37.9286。因此,在飞行时间>37.9286 h的情况下,该类备件需要携行。
(2)正态分布。以2组工作时间数据为例进行分析。第一组数据:35.38 h,30.01 h,26.48 h,40.26 h,37.63h,32.68 h,38.00 h,21.01 h,26.38 h,42.21 h,34.68 h,36.47 h。第二组数据:37.51 h,72.3 h,31.5 h,49.31 h,46.65 h,41.18 h,61.71 h,21.8 h,28.03 h,61.03 h,41.18。
对于正态分布函数,将数据带入2.1节(2)中的计算正态分布式中,可解得在0.05置信水平下的最优置信下限为0.925,可靠度在0.05置信水平下的最优置信下限为32.83 h。因此,在工作时间>32.83 h的情况下应当携行。
(3)威布尔分布。可靠寿命tR=γ+η(-1nR)1/m=γ+60.4006× 0.0514=3.1046+γ。其中γ是威布尔分布的位置参数,代表备件没发生故障的时间。由于在使用过程中,没有使用前备件就发生故障的情况,因此γ>0,也就是在时间t=γ之前,没有故障发生。的值能通过实际的工作经验确定得到一个确切值,也可通过估计来确定。在统计的最短的无故障工作时间区间是[21.0167,61.7167],则可靠寿命的取值范围是[24.1213,64.8213],所以可靠寿命的估计平均值是44.4731 h,若小于工作时间,则应携行。
3 结论
(1)对于有充足信息的备件,在0.05置信水平下,使用二项分布模型来求解,能够很好的反映在任务期间备件品种需求发生的概率,从而能够判断备件品种是否需要携行,经检验计算结果与实际情况相符。
(2)对于缺乏信息的备件,本文通过工作时间,来确定备件的寿命分布,客服了消耗数据缺乏的不利因素,通过寿命分布的方法,有效的解决了备件品种在0.05置信水平下的需求概率,从而确定备件是否需要携行。
(3)为了完善备件品种的需求计算方法,除了现有的消耗数据和工作时间数据,还需要对不同季节、不同地域等不同的使用环境下的消耗和工作时间数据展开收集。
[1]吴翔,李永乐,等.应用数理统计[M].长沙:科技大学出版社,2010.
[2]赵经成,祝华远,王文秀.航空装备技术保障运筹分析[M].北京:国防工业出版社,2010.
[3]冯静,孙权,罗鹏程等.装备可靠性与综合保障[M].长沙:国防科技大学出版社,2008.
[4]赵宇.可靠性数据分析[M].北京:国防工业出版社,2011.
[5]DarrenMcwhirt,JunyongAhn,Jennifers.shcme,KellyC.strong.Militaryconstructionprojects:comparisonofprojectdelivery methods[J].Jurnal of Facilities Mangements,2012:9:157-169.
[6]韩增奇,于俊杰,王朝阳.航空兵异地驻训航材需求预测模型[J].四川兵工学报,2010:(2):35-37.
[7]Mattthew Downing,Maxwell chipula and udechukwu Ojiako,Dinos kaparis.Forecasting in airforce supply chains[J].The International Journal of Logistics Management,2011:22(1):127-144.
〔编辑利文〕
TH7
B
10.16621/j.cnki.issn1001-0599.2016.12.56
