全唇裂腹鱼生长模型的筛选

王继隆，李雷，龚君华，张驰，马波

（1.中国水产科学研究院黑龙江水产研究所，黑龙江 哈尔滨 150070；2.西藏自治区农牧科学院水产科学研究所，西藏自治区 拉萨 850000）

全唇裂腹鱼生长模型的筛选

王继隆1，李雷1，龚君华2，张驰2，马波1

（1.中国水产科学研究院黑龙江水产研究所，黑龙江 哈尔滨 150070；2.西藏自治区农牧科学院水产科学研究所，西藏自治区 拉萨 850000）

2015年在西藏墨脱县布裙湖采捕到252尾全唇裂腹鱼Schizothorax integrilabiatus样本，通过耳石磨片观察分析其年龄组成，采用特殊Von Bertalanffy（VBGF）、Logistic、Gompertz和幂指数四个生长方程分别模拟全唇裂腹鱼的生长，利用最大似然法估计各模型的参数。结果表明：采集的样本共分为7个年龄组（即1～7龄），以2龄组数量最多。各模型的AIC（赤池信息量准则）和BIC（贝叶斯信息准则）值检验模型的拟合效果显示，VBGF生长方程最适合模拟全唇裂腹鱼的生长，其次为Gompertz、幂指数生长方程，而Logistic生长方程拟合效果最差。VBGF生长方程为：Lt=28.36×[1-e-0.14·（ti+0.57）]。由模型间AIC差值可知：Gompertz和Von Bertalanffy生长方程之间的模拟效果差别不太大，都能较好模拟全唇裂腹鱼的体长生长。

全唇裂腹鱼；耳石；年龄鉴定；模型检验

全唇裂腹鱼Schizothorax integrilabiatus属裂腹鱼亚科，裂腹鱼属Schizothorax，仅分布于雅鲁藏布江下游墨脱县境内海拔1 500m布裙湖及其周围山溪中[1,2]。与其他裂腹鱼类相比，该种地理分布区更狭小，种群数量更少，是裂腹鱼中的独特类群，在物种进化和资源保护中具有重要的研究意义。近年来，有关雅鲁藏布江的拉萨裂腹鱼Schizorax waltoni[6]、异齿裂腹鱼 Schizothorax onnori[7]、巨须裂腹鱼Schizothorax macropogon[8]、拉萨裸裂尻鱼Schizopygopsis younghusbandi[9]、双须叶须鱼Ptychobarbusdipogon[10]等裂腹鱼类的年龄与生长已有研究，为这些高原特有鱼类的保护研究积累了丰富的基础数据。但是，目前有关全唇裂腹鱼的研究极少，年龄与生长等生物学资料尚属空白。研究鱼类的年龄与生长是科学利用和有效保护渔业自然资源的生物学和生态学重要基础[3-5]。查明全唇裂腹鱼的年龄与生长可为该鱼种群动态变化及资源保护管理提供必要的生物学资料。

本试验采用耳石鉴定年龄，观察年轮的生长特征，选取Von Bertalanffy生长方程（VBGF）、逻辑斯谛生长方程（gistic GF）、Gompertz生长方程（GompertzGF）和幂指数生长方程分别模拟全唇裂腹鱼的生长，比较各模型的模拟效果[11]，筛选出最适合的生长方程，丰富全唇裂腹鱼的生物学资料，为渔业资源评估提供科学方法。

1 材料与方法

1.1 样本来源

试验样本于2015年4月采用刺网和电捕方法采集于西藏自治区林芝地区墨脱县布裙湖及入湖溪流中（图1）。共采集全唇裂腹鱼鱼标本252尾，部分样品现场解剖测量，剩余样品带回实验室，测量体长（精度0.1cm）、体质量（精度0.1g），同时采集微耳石鉴定年龄。

1.2 材料处理及数据分析

实验室将微耳石超声波清洗放入离心管中保存待测，检测时采用磨抛机（Struers LaboPol-35）对252个微耳石（左侧）进行磨抛，制作耳石装片，通过耳石轮纹观察鉴定全唇裂腹鱼的年龄。根据年龄鉴定的结果，结合体长、体质量数据分别采用VBGF、Logistic GF、Gompertz GF和幂指数生长方程进行生长模拟，具体公式如下：

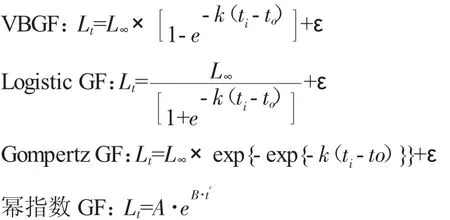
式中，L∞为渐近体长，K为生长曲线的平均速率，t0为假设的理论生长起点年龄，ε为加性误差（符合正态分布），A、B、C为幂指数方程中的参数。生长模型的参数采用最大似然进行估计，假设生长模型残差分布形式为正态分布，每个生长模型年龄体长数据的似然值可表示为：

模型采用AIC准则（赤池信息量准则）和BIC准则（贝叶斯信息准则）来筛选，AIC或BIC值最小者为最适模型。公式如下：

AIC=2lnL（p2，…，Pm,σ2）

BIC=2lnL（p2，…，Pm,σ2）+mln（n）

若模型误差服从独立正态分布，则AIC和BIC可表示为：

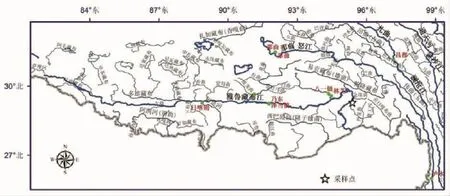
图1 调查点位置图Fig.1 The diagram of sampling sites

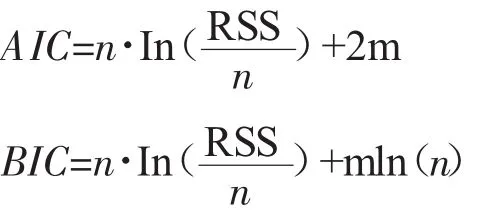
式中：m为模型参数；n为样本尾数；lnL（p1，…，pm，σ2）为似然值的对数。

2 结果与分析

2.1 年龄组成

年龄鉴定结果表明：252个全唇裂腹鱼样本共分为7个年龄组，即1～7龄。其中2龄鱼占30.95%，比例最高；其次为3龄鱼占23.41%，1龄鱼占17.86%；7龄鱼个体最少，占1.19%（表1）。

表1 布裙湖及入湖溪流中全唇裂腹鱼的年龄组成Tab.1 Age classes of Schizothorax integrilabiatus in Buqun Lake and lake stream

2.2 生长方程

四个生长方程对全唇裂腹鱼雌雄个体的统一检验结果表明：VBGF的AIC、BIC值最小；其次为Gompertz和幂指数生长模型；而logistic生长模型则表现最差（表2、图2）。因此，在描述全唇裂腹鱼体长生长时VBGF模型为最适模型，更能体现全唇裂腹鱼的生长特性。

表2 全唇裂腹鱼鱼参数比较与模型检验Tab.2 Comparison of parameters and growth model testing in Schizothorax integrilabiatus

图2 全唇裂腹鱼的体长生长曲线Fig.2 The growth curve of body length in Schizothorax integrilabiatus

3 讨论

鱼类的生理生长是同化作用与异化作业相互作用的结果，既有年际间的变化也有季节性波动，体现了其生活史的特征。鱼类生长作为重要的生物学指标是鱼类种群动态及渔业资源管理研究的基础。为了定量地分析鱼类的生长特征，一些数学模型引入到鱼类生长分析中。描述鱼类生长的模型多种多样的，各有侧重，因此模型的选择非常重要。目前关于全唇裂腹鱼的年龄与生长尚未见报道。为了更好地分析全唇裂腹鱼的生长特性，本文通过VonBertalanffy、Logistic、Gompertz和幂指数四个生长模型分别模拟布裙湖全唇裂腹鱼的生长，以各模型的AIC和BIC值判断最适生长模型。本研究结果表明，VBGF为最适生长模型，其次为Gompertz、幂指数，最后是Logistic生长模型，说明VBGF更能体现全唇裂腹鱼的生长特征。

一般认为，VBGF在分析鱼类体长生长时具有较强的适应性，在估算鱼类死亡参数和B-H动态综合模型中都是基于该模型参数[12,13]。应用VBGF的前提是鱼类生长应为匀速生长。本研究中，全唇裂腹鱼体长-体重关系中参数b为3.0528，t检验表明，b与3无显著差异[t=0.74＜t（0.05,252）］，表明全唇裂腹鱼的生长属于匀速生长。其他模型在模拟鱼类绝对增长方面具有更好的适应性。Gompertz生长方程为指数生长曲线，更适合生命周期短的r选择生物生长模拟，在本研究中其对全唇裂腹鱼的生长也表现了较好的适用性。Logistic生长方程较多地考虑了环境容纳量的问题[14]，在描述全唇裂腹鱼生长时适用性最差。幂指数生长方程在一定的假设条件下和VBGF方程式一致，这种特性也决定了其具有更广泛的适用性[15]。根据分析结果，表2中偏离值在Gompertz GF中最小，其次是Logistic GF，而VBGF中的偏差却最大（7.06cm）。因为VBGF模型属于单调渐进式方程，其极限体长一般要高于样本的最大观测值。Logistic和Gompertz生长方程属于近S型曲线，其偏离值比VBGF要小，而logistic生长方程容易低估LMax值，使得方程模拟值过于收敛[16]。幂指数生长方程和前三种模型差异较大，当模型参数C＞0，曲线呈单调上升，具指数曲线性质，无极限生长量；当C＜0，曲线呈S型，有极限生长量[15]。本研究中C值大于零，曲线呈指数型增长模式。由表2可见，Gompertz GF、幂指数GF、Logistic GF与BGF AIC差值△i分别为0.49、3.18、4.52。当△i＜2时，模型获得足够支持水平，可以考虑用于推断；当4＜△i＜7时，模型几乎得不到支持，模型间存在较大差异；当△i＞10时，模型得不到支持，足以证明模型间存在实质差异[17]。可见GompertzGF在模拟全唇裂腹鱼生长时也表现了较好的拟合效果，而Logistic GF效果较差。

全唇裂腹鱼的分布范围非常有限，仅分布在西藏林芝地区的山区湖泊、溪流中[2]，加之调查时间限制、采样难度大，故本研究采集样本数量有限，采集样本的最高年龄为7龄，且数量较少。本文仅是针对全唇裂腹鱼年龄与生长方面的初步研究，在今后西藏渔业资源调查时应不断补充各季节及雌性群体间的样本数量，为深入研究全唇裂腹鱼生物学特性积累丰富数据。

［1］武云飞,吴翠珍.青藏高原鱼类［M］.成都:四川科学技术出版社,1992.

［2］张春光,蔡斌,许涛清.西藏鱼类及其资源［M］.北京:中国农业出版社,1995.

［3］Beamish R J and Mcfarlane G A.The forgotten requirement forage validation in fisheries biology［J］.Transactions ofthe American Fisheries Society,1983,112（6）:735-743.

［4］殷名称.鱼类生态学［M］.北京:中国农业出版社,1995.

［5］陈毅峰,何德奎,曹文宣,等.色林错裸鲤的生长［J］.动物学报,2002,48（5）:667-676.

［6］Qiu H and Chen Y F.Age and growth of Schizorax waltoni intheYarlungTsangpoRiverinTibet,China［J］.Ichthyological Research,2009,56（3）:260-265.

［7］Bao-Shan Ma,Cong-Xin Xie,Bin Huo,et al.Age and growth of a long-lived fish Schizothorax connori in the YarlungTsangpoRiver,Tibet［J］.Zoological Studies,2010, 9（6）:749-759.

［8］朱秀芳,陈毅峰.巨须裂腹鱼年龄与生长的初步研究［J］.动物学杂志,2009,44（3）:76-82.

［9］Duan Y J,Xie C X,Zhou X J,et al.Age and growth characteristics of Schizopygopsis younghusbandi Regan,1905 in the Yarlung Tsangpo River in Tibet,China［J］.J A ppl Ichthyol,2014,30（5）:948-954.

［10］杨鑫,霍斌,段友健,等.西藏雅鲁藏布江双须叶须鱼的年龄结构与生长特征［J］.中国水产科学,2015,22（6）: 1085-1094.

［11］Katsanevakis S.Modelling fish growth:model selection, multi-model inference and model selection uncertainty［J］.Fisheries Research,2006,81（2-3）:229-235.

［12］Chen Y,Jackson A D and Harvey H H.A comparison of von Bertalanffy and polynomial functions in the modeling fish growth data［J］.Can J Fish Aquat Sci,1992,49（6）: 1228-1235.

［13］Morales-Nin B and Moranta J.Life history and fishery of thecommon dentex（Dentex dentex）in Mollorca（Balearic Islands,western Mediterranean）［J］.Fish Res,1997,30（1-2）:67-76.

［14］颜云榕,侯刚,卢伙胜,等.北部湾斑鳍白姑鱼的年龄和生长［J］.中国水产科学,2011,18（1）:145-155.

［15］陆小萏,陆文杰,郑光明,等.鱼类生长的幂指数生长方程［J］.水产学报,2002,3（26）:281-284.

［16］Urban H J.Modeling growth of different developmental stages in bivalves［J］.Marine Ecology Progress Series, 2002,238（1）:109-114.

［17］Burnham K P and Anderson D R.Model selection and multi-model inference:a practical information-theoretic approach［M］.NewYork:Springer,2002.

Selection of Growth Models for Schizothorax integrilabiatus

WANG Ji-Long1,LI Lei1,GONG Jun-Hua2,ZHANG Chi2,MA Bo1
（1.Heilongjiang River Fisheries Research Institute,Chinese Academy of Fishery Sciences,Harbin 150070,China; 2.Institute of Fishery Science,Tibet Academy of Agriculture and Animal Husbandry Sciences,Lhasa 850000,China）

Growth model was screened in 252 samples of Schizothorax integrilabiatus collected in Buqun Lake in Medog county,Tibet in 2015,by Von Bertalanffy,Logistic,Gompertz and power exponential growth models,according to the maximum likelihood estimation procedure was used to fit the functions.The growth of Schizothorax integrilabiatus was studied by otoliths and biological parameters to evaluate the age determination and growth simulation of Schizothorax integrilabiatus.The results showed that the fish samples were divided into 7 age classes including the fish from 1 year old to 7 years old,with dominant age of 2 years old in number.Based on the Akaike’s Information Criterion（AIC）,and Bayesian information criterion（BIC）,VBGF model was found to be the most appropriate growth model,followed by Gompertz,and power exponential growth equation,while logistic growth equation fitting effect was the worst.The VBGF function was described as:Lt=28.36×[1-e-0.14·（ti+0.57）].The difference in AIC value of the models revealed that the difference between Gompertz and Von Bertalanffy growth models was not significant,indicating that they can be used in simulation of the growth and stock resources and resource protection of Schizothorax integrilabiatus.

Schizothorax integrilabiatus;otolith;age determination;model checking

S965.199

A

1005-3832（2016）06-0010-04

2016-08-25

农业部公益性行业专项项目（201403012）；西藏自治区自然基金项目（14-45）.

王继隆（1984-）男，助理研究员，从事渔业资源与生态学研究.E-mail:wjl0321225@163.com

马波（1974-），男，研究员，从事渔业资源与生态学研究.E-mail:hsymabo@163.com