Rainbow Vertex-connection Number of Ladder and M¨obius Ladder

(Department of Mathematics,Qinghai Normal University,Xining810008,China)

Rainbow Vertex-connection Number of Ladder and M¨obius Ladder

LIU Hui-min,MAO Ya-ping

(Department of Mathematics,Qinghai Normal University,Xining810008,China)

A vertex-colored graphGis said to berainbow vertex-connectedif every two vertices ofGare connected by a path whose internal vertices have distinct colors,such a path is called a rainbow path.Therainbow vertex-connection numberof a connected graphG,denoted byrvc(G),is the smallest number of colors that are needed in order to makeGrainbow vertex-connected.If for every pairu,vof distinct vertices,Gcontains a rainbowu-vgeodesic,thenGisstrong rainbow vertex-connected.The minimum numberkfor which there exists ak-vertex-coloring ofGthat results in a strongly rainbow vertex-connected graph is called thestrong rainbow vertex-connection numberofG,denoted bysrvc(G).Observe thatrvc(G)≤srvc(G)for any nontrivial connected graphG.In this paper,for a LadderLn, we determine the exact value ofsrvc(Ln)forneven.Fornodd,upper and lower bounds ofsrvc(Ln)are obtained.We also give upper and lower bounds of the(strong)rainbow vertex-connection number of M¨obius Ladder.

vertex-coloring;rainbow vertex-connection;(strong)rainbow vertex-connection number;Ladder;M¨obius Ladder

§1.Introduction

All graphs considered in this paper are fnite,undirected and simple.We follow the notation and terminology of Bondy and Murty[1],unless otherwise stated.Consider an edge-coloring(not necessarily proper)of a graphG=(V,E).We say that a path ofGis rainbow,if no two edgeson the path have the same color.An edge-colored graphGisrainbow connectedif every two vertices are connected by a rainbow path.An edge-coloring is astrong rainbow coloringif between every pair of vertices,one of their geodesics,i.e.,shortest paths,is a rainbow path. The minimum number of colors required to rainbow color a graphGis calledthe rainbow connection number,denoted byrc(G).Similarly,the minimum number of colors required to strongly rainbow color a graphGis called thestrong rainbow connection number,denoted bysrc(G).Observe thatrc(G)≤src(G)for every nontrivial connected graphG.The notions of rainbow coloring and strong rainbow coloring were introduced by Chartrand et al[5].There are many results on this topic,we refer to[3-4].

In[7],Krivelevich and Yuster proposed a similar concept,the concept of rainbow vertexconnection.A vertex-colored graphGisrainbow vertex-connectedif every two vertices are connected by a path whose internal vertices have distinct colors,and such a path is called a rainbow path.Therainbow vertex-connection numberof a connected graphG,denoted byrvc(G),is the smallest number of colors that are needed in order to makeGrainbow vertexconnected.Note the trivial fact thatrvc(G)=0 if and only ifGis a complete graph(here an uncolored graph is also viewed as a colored one with 0 color).Also,clearly,rvc(G)≥diam(G)-1 with equality if the diameter is 1 or 2.In[6],the authors considered the complexity of determining the rainbow vertex-connection of a graph.In[7]and[9],the authors gave bounds forrvc(G)in terms of the minimum degree ofG.

Li et al[8]introduced the concept of strong rainbow vertex-connection.A vertex-colored graphGisstrongly rainbow vertex-connected,if for every pairu,vof distinct vertices,there exists a rainbowu-vgeodesic.The minimum numberkfor which there exists ak-coloring ofGthat results in a strongly rainbow vertex-connected graph is calledthe strong rainbow vertexconnection numberofG,denoted bysrvc(G).Similarly,we havervc(G)≤srvc(G)for every nontrivial connected graphG.Furthermore,for a nontrivial connected graphG,we have

where diam(G)denotes the diameter ofG.The following results onsrvc(G)are immediate from defnition.

For more results on the rainbow connection and rainbow vertex-connection,we refer to the survey[10]and a new book[11]of Li and Sun.

For an integern≥3,theladder Lnof order 2nis a cubic graph obtained from two cyclesandwithandby adding one edge betweenuiandvifor 1≤i≤n.TheM¨obius ladder Mnof order 2nis obtained from the ladderLnby deleting the edgesu1unandv1vnand then adding the edgesu1vnandunv1.Take for example,L5,L7,M4,M5are shown in Figure 1.

The following propositions are immediate.

Proposition 1LetLnbe a ladder of order 2n.Then

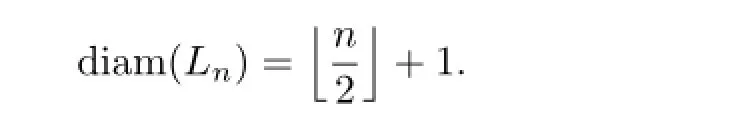
Figure 1 Rainbow Vertex-colorings ofL5andL7

Proposition 2LetMnbe a M¨obius ladder of order 2n.Then

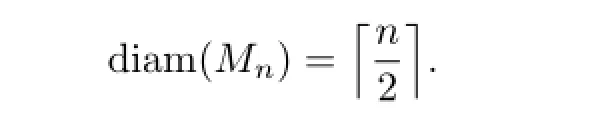
Cai et al[2]studied the(strong)rainbow vertex-connection numbers of of ladders and M¨obius ladders.In this paper,we investigate the(strong)rainbow vertex-connection number of of ladders and M¨obius ladder.This paper is organized as follows.In Section 1,we obtain the exact value ofsrvc(Ln)forneven,and give sharp upper and lower bounds ofsrvc(Ln)fornodd.We give sharp upper and lower bounds ofsrvc(Mn).

§2.Rainbow Vertex-connection Number of Ladders

At frst,we focus on the caseneven.

Theorem 1LetLnbe a ladder of order 2n(n≥4)ifnis an even integer.Then

It sufces to show that for any two verticesx,y∈V(G),there is a rainbowx-ygeodesic inGunder the above vertex-coloring.Clearly,iforthere exists a rainbowx-ygeodesic contained in the cycleor.We consider the following four cases to show this theorem.

Without loss of generality,letx=ui,y=vj.Ifi＜j,thendG(x,y)=dG(ui,vj)=j-i+1 and hence the pathui,ui+1,···,uj,vjis a rainbowui-vjgeodesic,as desired.Ifj＜i,thendG(x,y)=dG(ui,vj)=i-j+1 and hence the pathvj,vj+1,···,vi,uiis a rainbowvj-uigeodesic,as desired.

Figure 2 (a)The Rainbow Vertex-coloring ofLnfornEven(b)The Rainbow Vertex-coloring ofLnfornOdd

Without loss of generality,letx=ui,y=vj.Ifi＜j,thendG(x,y)=dG(ui,vj)=j-i+1 and hence the pathui,ui+1,···,uj,vjis a rainbowui-vjgeodesic,as desired.Ifj＜i,thendG(x,y)=dG(ui,vj)=i-j+1 and hence the pathvj,vj+1,···,vi,uiis a rainbowvj-uigeodesic,as desired.

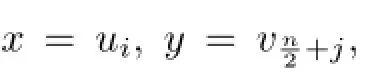
Next,we are in a position to show the casenodd.

Theorem 2LetLnbe a ladder of order 2n(n≥3).Ifnis odd,then

Moreover,the lower bound is sharp.

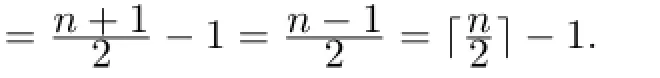
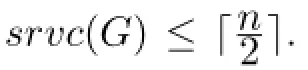
It sufces to show that for any two verticesx,y∈E(G),there is a rainbowx-ygeodesic inGunder the above vertex-coloring.Clearly,iforthere exists a rainbowx-ygeodesic contained in the cycleor.We consider the following four cases to show this theorem.

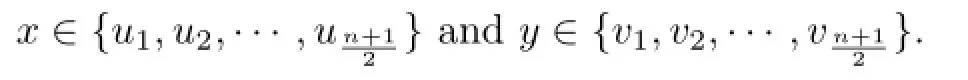
Without loss of generality,letx=ui,y=vj.Ifi＜j,thendG(x,y)=dG(ui,vj)=j-i+1 and hence the pathui,ui+1,···,uj,vjis a rainbowui-vjgeodesic,as desired.Ifj＜i,thendG(x,y)=dG(ui,vj)=i-j+1 and hence the pathvj,vj+1,···,vi,uiis a rainbowvj-uigeodesic,as desired.

Without loss of generality,letx=ui,y=vj.Ifi＜j,thendG(x,y)=dG(ui,vj)=j-i+1 and hence the pathui,ui+1,···,uj,vjis a rainbowui-vjgeodesic,as desired.Ifj＜i,thendG(x,y)=dG(ui,vj)=i-j+1 and hence the pathvj,vj+1,···,vi,uiis a rainbowvj-uigeodesic,as desired.

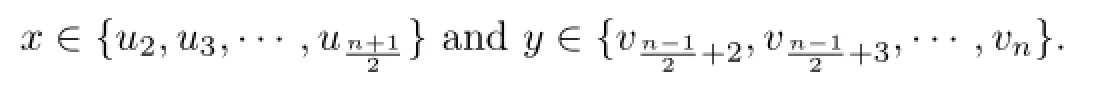
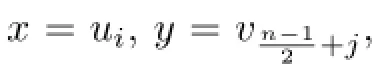
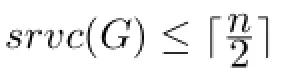
To show the sharpness of the bounds of this theorem,we consider the graphL5andL7. Observe thatrvc(G)=1 if and only if diam(G)=2.Clearly,rvc(L3)=1.It is easy to check that the vertex-colorings ofL5andL7shown in Figure 1 are rainbow vertex-colorings.

Sorvc(L5)≤2 andrvc(L7)≤3.Combining this with(1),we know thatrvc(L5)=2 andrvc(L7)=3,which implies that the lower bound of Theorem 2 is sharp.

§3.Rainbow Vertex-connection Number of M¨obius Ladder

In this section,we consider the rainbow vertex-connection number of M¨obius ladder.

Theorem 3LetMnis a M¨obius ladder of order 2n(n≥3).Then

ProofWe distinguish the following two cases to prove this theorem.

Case 1nis even.

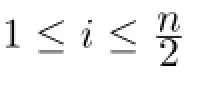
Figure 3 (a)The Rainbow Coloring ofMnfornEven(b)The Rainbow Coloring ofMnfornOdd

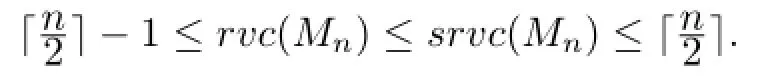
Case 2nis odd.

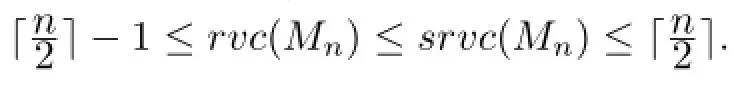
One can easily check that the graphsM4andM5attain the lower bound of this theorem.

AcknowledgmentThe authors are grateful to the referees’valuable comments and suggestions,which helped to improve the presentation of this paper.

[1]BONDY J A,MURTY U S R.Graph Theory[M].GTM 244,New York:Springer,2008.

[2]CARO Y,LEV A,RODITTY Y,et al.On rainbow connection[J].Electron J Combin,2008,15:R57.

[3]CHAKRABORTY S,FISCHER E,MATSLIAH A,et al.Hardness and algorithms for rainbow connectivity[J].J Combin Optim,2011,21:330-347.

[4]CHARTRAND,JOHNS,KATHLEEN A M,et al.Rainbow connection in graphs[J].Math Bohem,2008, 133:85-98.

[5]CHEN Li-li,LI Xue-liang,SHI Yong-tang.The complexity of determining the rainbow vertex-connection of a graph[J].Theoret Comput Sci,2011,412:4531-4535.

[6]KRIVELEVICH M,YUSTER R.The rainbow connection of a graph is(at most)reciprocal to its minimum degree three[J].IWOCA 2009,LNCS,2009,5874:432-437.

[7]LI Xue-liang,MAO Ya-ping,SHI Yong-tang.The strong rainbow vertex-connection of graphs[J].Utilitas Math,2014,93:213-223.

[8]LI Xue-liang,SHI Yong-tang.On the rainbow vertex-connection[J].Discuss Math Graph Theory,2013, 33(2):307-313.

[9]LI Xue-liang,SHI Yong-tang,SUN Yue-fang.Rainbow connections of graphs:A survey[J].Graphs Combin, 2013,29(1):1-38.

[10]LI Xue-liang,SUN Yue-fang.Rainbow Connections of Graphs[M].New York:Springer,2012.

O157.5

:A

1002–0462(2016)04–0399–07

Received date:2014-07-31

Foundation item:Supported by the National Natural Science Foundation of China(11551001,11061027, 11261047,11161037,11461054);Supported by the Science Found of Qinghai Province(2016-ZJ-948Q,2014-ZJ-907)

Biography:LIU Hui-min(1969-),female,native of Nanyang,Henan,an associate professor of Qinghai Normal University,M.S.D.,engages in graph theory and combinatorial optimization.

2000 MR Subject Classifcation:05C15,05C40