Composition and Multiplication Operators on Lp,∞(M)

(College of Mathematics and Systems Science,Xinjiang University,Urumqi830046,China)

Composition and Multiplication Operators on Lp,∞(M)

HAN Ya-zhou

(College of Mathematics and Systems Science,Xinjiang University,Urumqi830046,China)

We give some properties of the composition and multiplication operators onLp,∞(M),whereMis a semifnite von Neumann algebra with a normal semifnite faithful traceτ.

von Neumann algebras;composition operators;multiplication operators;noncommutative weakLpspaces

§1.Introduction

Let(Ω,Σ,ν)be a complete measure space andL0(Ω)be the space of all classes ofνmeasurable real-valued functions defned on Ω.Letf∈L0(Ω).Recall that the distribution function offis defned as

and its nonincreasing rearrangement is defned as

For a measurable functionfon(Ω,Σ,ν),we defne

The classical weakLpspaceLp,∞(Ω)is defned as the set of all measurable functionsfon (Ω,Σ,ν)such that‖f‖p,∞＜∞.

Let(Ω1,Σ1,ν1)and(Ω2,Σ2,ν2)be two measure spaces andT:Y⊆Ω2→Ω1be a measurable transform.We defne the linear transformationCTfromLp,∞(Ω1)intoL0(Ω2) as

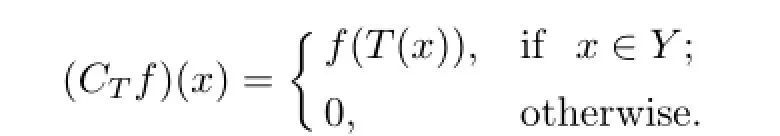
On the other hand,we defne the multiplication operators onLp,∞(Ω1)byTg(f)=fg,wheregis a measurable function on Ω1.ThenTgmapsLp,∞(Ω1)intoL0(Ω1).For further results about composition and multiplication operators,the reader is referred to[1-2].

In 1999,Labuschagne[3]introduced the concept of composition operators on noncommutativeLpspaces and obtained a series of results about composition operators on these spaces. Subsequently,Labuschagne and Majewski[4]extended it to the case of noncommutative Orlicz spaces.

In this article we introduce the multiplication and composition operators on noncommutative weakLpspaces.By adapting the techniques in[3-4],we obtain some properties of multiplication and composition operators on noncommutative weakLpspaces.

§2.Preliminaries

We use standard notions from theory of noncommutativeLp-spaces.Our main references are[5-7].LetMbe a semifnite von Neumann algebra acting on a Hilbert spaceHwith a normal semifnite faithful traceτ.We denote byP(M)the complete lattice of all(self-adjoint) projections inM.For everyx∈B(H),there is a unique polar decompositionx=u|x|,where|x|∈B(H)+(the positive part ofB(H))anduis a partial isometry operator.Letr(x)=u∗uandl(x)=uu∗.We callr(x)andl(x)the right and left supports ofx,respectively.Ifxis self-adjoint,thenr(x)=l(x).This common projection is then said to be the support ofxand denoted bys(x).

The closed densely defned linear operatorsxinHwith domainD(x)is said to be afliated withMif and only ifu∗xu=xfor all unitary operatorsuwhich belong to the commutantM′ofM.Whenxis afliated withM,xis said to beτ-measurable if for everyε＞0 there exists ae∈P(M)such thate(H)⊆D(x)andτ(e⊥)＜ε(where for any projectionewe lete⊥=I-e). The set of allτ-measurable operators will be denoted byL0(M).The setL0(M)is a∗-algebra with sum and product being the respective closure of the algebraic sum and product.The topology ofL0(M)is determined by the convergence in measure.The traceτcan be extended to the positive coneL0(M)+ofL0(M)

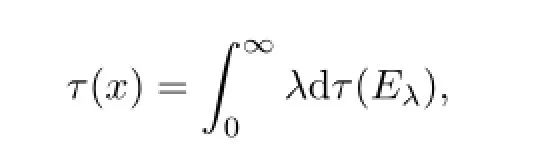
whereis the spectral decomposition ofx.For 0＜p＜∞,let

We defne

Then(Lp(M);‖·‖p)is a Banach(or quasi-Banach forp＜1)space.As usual,we putL∞(M)=Mand denote by‖·‖∞(=‖·‖)the usual operator norm.Forx∈L0(M)we defne

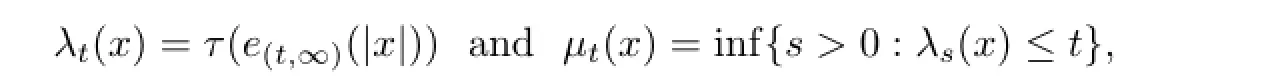
wheree(t,∞)(|x|)is the spectral projection of|x|associated with the interval(t,∞).The functiont→λt(x)is called the distribution function ofxandt→µt(x)is the generalized singular number ofx.We will denote simply byλ(x)andµ(x)the functionst→λt(x)andt→µt(x),respectively.It is easy to check that both are decreasing and continuous from the right on(0,∞).We refer to[8-9]for more information.

We defne the noncommutative weakLpspacesLp,∞(M)by

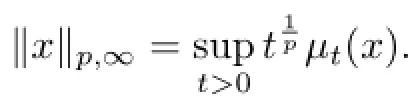
Proposition 1

1.Ifx∈Lp,∞(M)andτ(s(|x|))＜∞,thenx∈Lq(M)for allq＜p＜∞.

2.Ifx∈Lp,∞(M)∩M,thenx∈Lq(M)for allq＞p.

3.Ifx∈Lp0,∞(M)∩Lp1,∞(M)withp0＜p＜p1,thenx∈Lp(M).

4.If 0＜p0＜p＜p1≤∞,thenLp,∞(M)⊆Lp0(M)+Lp1(M).

Proof(1)Letp＜∞.By Lemma 3(ii)of[11],we have

This impliesx∈Lq(M).

(2)Letx∈Lp,∞(M)∩M.It is clear that

Thusx∈Lq(M).

(3)Givenx∈Lp0,∞(M)∩Lp1,∞(M),we writee1=e[0,1](|x|)ande2=e(1,∞)(|x|).Therefore,x=xe1+xe2andx1=xe1∈Lp0,∞(M),x2=xe2∈Lp1,∞(M).It follows from(1)and (2)thatx1∈Lp(M)andx2∈Lp(M).Thusx∈Lp(M).

(4)It follows immediately from(1)and(2).

§3.Multiplication Operators on Lp,∞(M)

Leta∈L0(M).The transformation:x→axand,x∈Lp,∞(M)are called left and right multiplication operators,respectively.For systematic study of the multiplication operators on diferent classical function spaces we refer to[12-14].

Proposition 2Let 0＜p＜∞anda∈L0(M).Then the left multiplication operatoris bounded if and only ifa∈M.Moreover,

ProofFora∈M,we have

and soConversely,fora∈L0(M),we writen=1,2,···.By Proposition 21 of[6],there existsn0∈N+such thatτ(en0)＜∞and soτ(en)＜∞for alln≥n0.Now,we suppose thatais an unbounded operator,then the projectionenhas positive trace for infnitely manyn∈N+.Without loss of generality we suppose that 0＜τ(en)＜∞for alln∈N+.LetThen

Therefore

a contradiction.Thusa∈M.Moreover,ifa∈M,then arguing as before

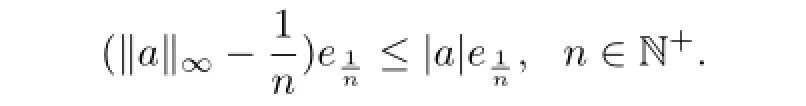
Thus

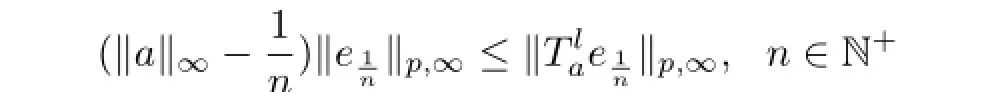
Remark 1

1.The right multiplication operatoronLp,∞(M)is bounded if and only ifa∈M.Moreover,

2.The set of all left(respectively,right)multiplication operators onLp,∞(M)is a subalgebra ofB(Lp,∞(M)).

3.Letx∈Lp,∞(M)and letNbe a von Neumann subalgebra ofMcontaining the spectral projections of|x|.PutthenA1andA2are abelian subalgebras ofB(Lp,∞(M)).

Proposition 3Forε＞0 anda∈M,we setandThenis a closed subspace ofLp,∞(M).

ProofIfxis an operator belonging to be the closure ofthen there exists a sequencesuch that‖x-xn‖p,∞→0,n→∞.Thus,for anyη＞0,there existsn0∈N+such thatThis means that

Therefore,(1-eε)x=0 and henceThis completes the proof.

Theorem 1Let 0≤a∈M.Thenis compact if and only ifis fnite dimensional for allε＞0,where

ProofFirst we assume that:E(M)→E(M)is a compact operator.We consider the bounded operatoriε:given byiεx=eεx.Clearly,iεis continuous and hence the compositionis a compact operator.Therefore,is a compact operator.

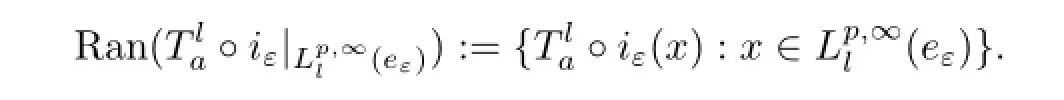
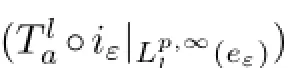
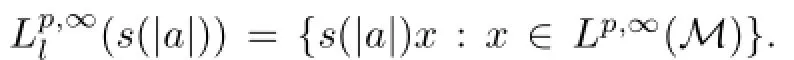
ProofSuppose thatη＞0 such that|a|≥ηs(|a|).Forx∈Lp,∞(M),we have

Consequently,has closed range on

§3.Composition Operators on Lp,∞( M)

A Jordan morphism between two von Neumann algebraM1andM2is a linear mappingJ:M1→M2which preserves the Jordan product,i.e.,J(ab+ba)=J(a)J(b)+J(b)J(a)for alla,b∈M1.In the sequel,by the term Jordan*-morphism we understand a map fromM1intoM2which preserves adjoints and Jordan product of elements.A linear mapJ:M1→M2is called normal ifJis bounded andσ-continuous(see[7]).For further results about Jordan morphism,the reader is referred to[3-4,7,15].

A weight on a von Neumann algebraMis a mapφfromM+(the positive part ofM)to [0,∞]satisfyingφ(αx)=αφ(x)andφ(x+y)=φ(x)+φ(y),whereα∈R+,x,y∈M+.

We say thatτ2◦Jisε-δabsolutely continuous with respect toτ1,if for anyε＞0 there existsδ＞0 such that,for any projectione∈P(M1),we haveτ2(J(e))＜ε,wheneverτ1(e)＜δ.

Defnition 1LetM1andM2be semifnite von Neumann algebras equipped with normal semifnite faithful traceτ1andτ2,respectively.LetJ:M1→M2be a normal Jordan*-morphism andτ2◦Jisε-δabsolutely continuous with respect toτ1.If the unique continuous extension(in measureable topology):L0(M1)→L0(M2)mapsLp,∞(M1)intoLp,∞(M2),we call the induced linear mapLp,∞(M1)→Lp,∞(M2)a composition operator fromLp,∞(M1) intoLp,∞(M2)and we will occasionally denote it byCJ.

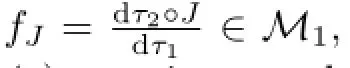
ProofSinceτ2◦Jisε-δabsolutely continuous with respect toτ1,it follows from Proposition 4.1 of[4](or,Proposition 4.7 of[3])thatJextends uniquely to a Jordan*-morphism fromL0(M1)toL0(M2),which is continuous under the measure topology.We will consistently writeJfor this extension.Givenx∈Lp,∞(M1)withx=x∗and‖x‖p,∞＜1.First,we showJ(x)∈Lp,∞(M2).By approximation with polynomials we obtainJ(|x|p)=J(|x|)p.Sincex=x∗,we have

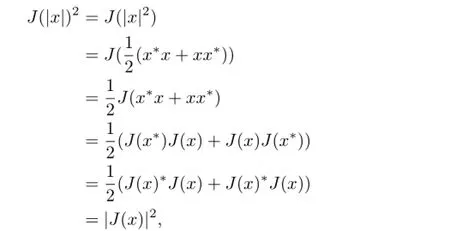
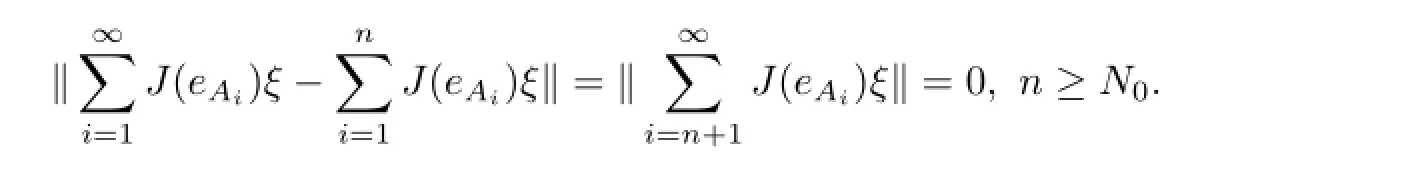
Therefore,J(eλ(|x|))is a spectral family.Combining the fact

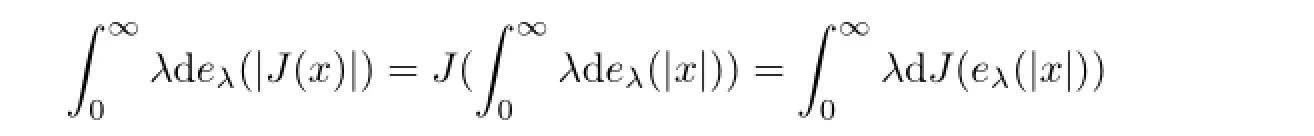
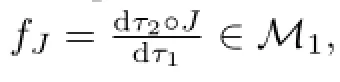
and so

This implies thatJmaps the self-adjoint portion ofLp,∞(M1)intoLp,∞(M2).Moreover,JmapsLp,∞(M1)intoLp,∞(M2).It follows from the closed graph theorem(cf[17])thatJrestricts to a bounded operatorCJfromLp,∞(M1)intoLp,∞(M2).

Letx∈L0(M)and 0＜p,q≤∞.DefneLp,q(M)is defned as the space of allx∈L0(M)such that‖x‖p,q＜∞.The spacesLp,q(M) are quasi-Banach spaces with the quasi-norm‖x‖p,q(cf[10]).By Proposition 1.2 in[10]and Proposition 1.4.9 in[1],we have

Theorem 2LetM1andM2be semifnite von Neumann algebras equipped with normal semifnite faithful traceτ1andτ2,respectively.LetJ:M1→M2be a normal Jordan*-morphism andε-δabsolutely continuous with respect toτ1,then the following two statements are equivalent

(ii)Jextends uniquely to a continuous*-morphism fromL0(M1)toL0(M2),restricts to a bounded mapCJfromLp,q(M1)toLp,q(M2)for all 0＜p＜∞,0＜q≤∞.

ProofA similar discussion to the proof of Proposition 5 shows that(i)implies(ii). Conversely,letp=q=1.It follows from(ii)that there exists a constantc＞0 such thatfor eachx∈L1(M1).By Proposition6.5of[16],we obtainfort＞0 large enough,wheree(t,∞)(fJ)is the spectral projection offJcorresponding to the interval(t,∞).Sincewe havefort＞0 large enough.That isfJisτ1measurable.Now,letandy∈M1∩L1(M1)with.Ifbe the polar decomposition offJeny,thenandTherefore,

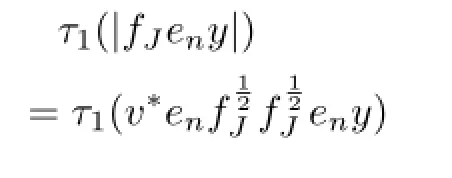
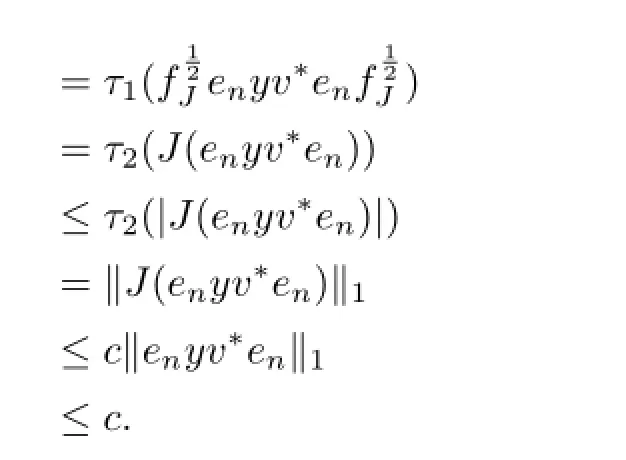
SinceM1∩L1(M1)is dense inL1(M1),we deduce thatfJen∈M1and‖fJen‖∞≤c.This ensures thatfJ∈L1(M1)∗=M1(cf[7]).

[1]GRAFAKOS L.Classical Fourier Analysis[M].New York:Springer,2008.

[2]CASTILLO R,NARVAEZ F,FERNANDE Z.Multiplication and composition operators on wekLpspales[J]. Bulletin of the Malaysian Mathematical Sciences Society,2015,38:927-973.

[3]LABUSCHAGNE L E.Composition operators on non-commutativeLp-spaces[J].Expo Math,1999,17: 429-468.

[4]LABUSCHAGNE L E,MAJEWSKI W A.Maps on noncommutative orlicz spaces[J].Illinois J Math,2011, 55:1053-1081.

[5]PISIER G,XU Quan-hua.NoncommutativeLp-spaces,in:Handbook of the Geometry of Banach Spaces[M]. Amsterdam:North-Holland Publ Co,2003,2:1459-1517.

[6]TERP M.LpSpaces Associated with Von Neumann Algebras[N].Copenhagen:Copenhagen Univ,1981.

[7]XU Quan-hua,BEKJAN T N,CHEN Ze-qian.Introduction to Operator Algebras and NoncommutativeLpSpaces(Chinese)[M].Beijing:Science Press,2010.

[8]FACK T,KOSAKI H.Generalizeds-numbers ofτ-measurable operators[J].Prac J Math,1986,123:269-300.

[9]WU Tian-feng,ZHOU Jia,WANG Yun-xia.Non-commutative Kolmogorov inequality and Zygmund inequality[J].Chin Quart J of Math,2012,27(1):104-109.

[10]HAN Ya-zhou,BEKJAN T N.The dual of noncommutative lorentz spaces[J].Acta Math,2011,31B:2067-2080.

[11]BEKJAN T N.Hardy-Littlewood maximal function ofτ-measurable operators[J].J Math Anal Appl,2006, 322:87-96.

[12]ARORA S C,DATT G,VERMA S.Multiplication operators on Lorentz spaces[J].Indian Journal of Mathematics,2006,48:317-329.

[13]ABRAHAMESE M B.Multiplication Operators[A].New York:Springer Verlag,1978,17-36.

[14]KOMAL B S,GUPTA S.Multiplication operators between Orlicz spaces[J].Integral Equations and Operator Theory,2001,41:324-330.

[15]JACOBSON N,RICKART C E.Jordan homomorphisms of rings[J].Tran Ame Math Soc,1950,69:479-502.

[16]PEDERSEN G K,TAKESAKI M.The Radon-Nikodym theorem for von Neumann algebras[J].Acta Math, 1973,130:53-87.

[17]KALTON N J,PECK N T,ROBERTS J W.An F-space Sampler[M].London:Cambridge University Press, 1984.

O177.1

:A

1002–0462(2016)04–0340–09

Received date:2014-05-27

Foundation item:Supported by the National Natural Science Foundation of China(11371304,11401507)

Biography:HAN Ya-zhou(1982-),male,native of Shangqiu,Henan,a lecturer of Xinjiang University,Ph.D., engages in functional analysis.

2000 MR Subject Classifcation:46L52,46L51