On the Growth of Solutions of a Class of Higher Order Linear Diferential Equations

(College of Mathematics and Information Science,Jiangxi Normal University,Nanchang330022, China)

On the Growth of Solutions of a Class of Higher Order Linear Diferential Equations

XIONG Hui,LIU Hui-fang

(College of Mathematics and Information Science,Jiangxi Normal University,Nanchang330022, China)

In this paper,we investigate the growth of solutions of the diferential equationsf(k)+Ak-1(z)f(k-1)+···+A0(z)f=0,whereAj(z)(j=0,···,k-1)are entire functions. When there exists some coefcientAs(z)(s∈{1,···,k-1})being a nonzero solution off′′+P(z)f=0,whereP(z)is a polynomial with degreen(≥1)andA0(z)satisfesσ(A0)≤1/2 or its Taylor expansion is Fabry gap,we obtain that every nonzero solution of such equations is of infnite order.

entire function;diferential equation;growth of order

§1.Introduction and Main Results

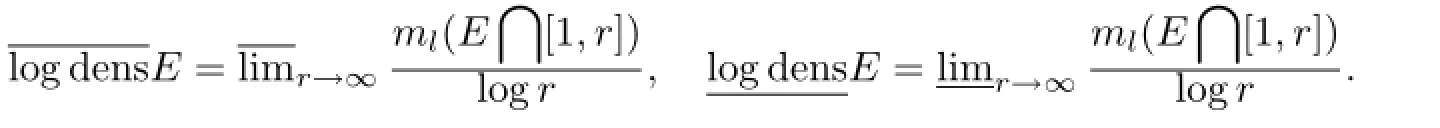
Consider the homogeneous linear diferential equation

whereA0(z),A1(z),···,Ak-1(z)are entire functions.If all the coefcientsAj(z)(j=0,···,k-1)are polynomials,then every nonzero solution of Eq(1.1)is of fnite order(see[3-4]).Ifsis the largest integer such thatAs(z)is transcendental,it is well known that there exists at mostslinearly independent fnite order solutions of Eq(1.1).It tells us that most of the solutions of Eq(1.1)are of infnite order when at least one of the coefcientsAj(z)is transcendental.

Thus,a natural question is:what conditions on coefcientsAj(j=0,···,k-1)will guarantee that every nonzero solution of Eq(1.1)has infnite order?This question has attracted great interest(see[5-10]).In which,Chen and Yang proved the following result.

Theorem A[5]Suppose thatA0(z)(/≡0),A1(z),···,Ak-1(z)are entire functions and max{σ(Aj):1≤j≤k-1}＜σ(A0)＜+∞,then every nonzero solution of Eq(1.1)has infnite order.

When the dominant coefcientA0(z)in Theorem A is changed to any coefcientAd(z)(d∈{0,···,k-1}),Hellerstein,Miles and Rossi obtained the following result.

Theorem B[6]Suppose thatA0(z),A1(z),···,Ak-1(z)are entire functions.If there exists somed∈{0,···,k-1}such that max{σ(Aj):j/=d}＜σ(Ad)≤1/2,then every solution of Eq(1.1)is either a polynomial or a transcendental entire function of infnite order.

From Theorem B,we know that the above result may be invalid when the coefcientAd(z) satisfesσ(Ad)＞1/2.For example,f(z)=eiz+1 satisfes the equationf′′′+(e-iz+1)f′′+f′+f=0.Hereσ(e-iz+1)=1＞1/2 andσ(f)=1.Thus,a question arises:whenσ(Ad)＞1/2 and max{σ(Aj):j/=d}＜σ(Ad),what else conditions on coefcients will guarantee that every nonzero solution of Eq(1.1)is of infnite order.Recently,Wu investigated the above problem in[11].In fact,they studied the growth of solutions of the equation

where the coefcientA1(z)is a nonzero solution of the equationf′′+P(z)f=0,hereP(z)is a polynomial with degreen≥1 and obtained the following result.

Theorem C[11]Suppose thatA1(z)is a nonzero solution of the equationf′′+P(z)f=0, whereP(z)=anzn+···+a0is a polynomial with degreen≥1 andA0(z)is a transcendental entire function ofσ(A0)≤1/2,then every nonzero solutionfof Eq(1.2)satisfesσ(f)=∞.

Later on,Zhang and Wu extended Theorem C to the higher order linear diferential equation, and obtained the following result.

Theorem D[12]Suppose thatA1(z)is a nonzero solution of the equationf′′+P(z)f=0, whereP(z)=anzn+···+a0is a polynomial with degreen≥1 andAj(z)(/≡0)(j=0,2,···,k-1)are entire functions satisfying max{σ(Aj):2≤j≤k-1}＜σ(A0)≤1/2,then every nonzero solutionfof Eq(1.1)satisfesσ(f)=∞.

Note that in theorems C and D,among the coefcients of Eq(1.1),A1(z)is the dominant coefcient and a nonzero solution of the equationf′+P(z)f=0,and the coefcientA0(z) satisfesσ(A0)≤1/2＜σ(A1).It is natural to pose the following questions.

Question 1.1If the dominant coefcient of Eq(1.1)isAs(z)(s∈{2,···,k-1})andAs(z)is a nonzero solution of the equationf′′+P(z)f=0,would every nonzero solution of Eq(1.1)still have infnite order?

Question 1.2If the coefcient of Eq(1.1)As(z)(s∈{1,···,k-1})is a nonzero solution of the equationf′′+P(z)f=0,and the coefcientA0(z)satisfesσ(A0)＞1/2 andσ(A0)/=σ(As), would every nonzero solution of Eq(1.1)still have infnite order?

In this paper,we investigate the above questions and obtain the following results.

Theorem 1.1Suppose thatA0(z),A1(z),···,Ak-1(z)are entire functions.If there exists somes∈{2,···,k-1}such thatAs(z)is a nonzero solution of the equationω′′+P(z)ω=0, whereP(z)=anzn+···+a0is a polynomial with degreen≥1 andAj(z)(j/=s)satisfy

then every nonzero solutionfof Eq(1.1)satisfesσ(f)=∞.

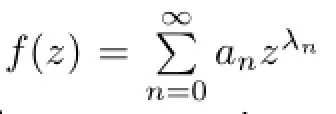
Theorem 1.2Suppose thatA0(z),A1(z),···,Ak-1(z)are entire functions.If there exists somes∈{1,···,k-1}such thatAs(z)is a nonzero solution of the equationω′′+P(z)ω=0, whereP(z)=anzn+···+a0is a polynomial with degreen≥1 andA0(z)is a Fabry gap series satisfyingσ(A0)/=σ(As)and

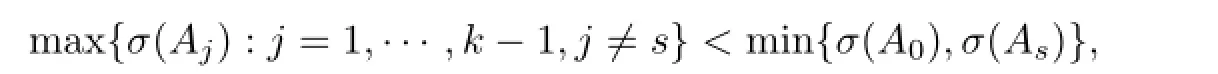
then every nonzero solutionfof Eq(1.1)satisfesσ(f)=∞.

In the sequel,we construct an example to show thatA0(z)is a Fabry gap series andσ(A0)＞1/2.

Remark 1.1Theorem 1.1 shows that the answer to Question 1.1 is afrmative.As for Question 1.2,we know that the conclusion may be valid from Theorem 1.2 and Example 1.1, but we do not know whether the conclusion is universal.

§2.Lemmas

In order to prove our theorems,we need the following defnitions and lemmas.

Letf(z)be an entire function of fnite positive order,S={z:α≤argz≤β}(0＜β-α＜2π).If for eachθ∈(α,β),the following equality holds

then we say thatf(z)exponentially tends to infnity in the angular domainS.If for eachθ∈(α,β),the following equality holds

then we say thatf(z)exponentially tends to zero in the angular domainS.

Lemma 2.1[14]Letω(z)be a transcendental meromorphic function of fnite orderσin the complex plane,Γ={(k1,j1),···,(km,jm)}be a fnite set of distinct pairs of integers that satisfeski＞ji≥0(i=1,···,m)and letε＞0 be a given constant,then the following three statements hold.

(i) There exists a setE1⊂[0,2π)that has linear measure zero,such that ifψ0∈[0,2π)E1, then there exists a constantR0=R(ψ0)＞0 such that for allzsatisfying argz=ψ0and|z|≥R0,and for all(k,j)∈Γ,we have

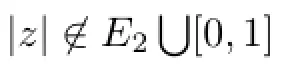
Lemma 2.2[15]Letf(z)be a nonzero solution of the equationf′′+P(z)f=0,whereP(z)=anzn+···+a0is a polynomial of degreen≥1 and let

wherej=0,1,···,n+1,thenf(z)has the following properties.

(i) In each angular domainSj,fexponentially tends to infnity either,or exponentially tends to zero.

(ii) Iffexponentially tends to zero in the angular domainSj,thenfexponentially tends to infnity in the angular domainsSj-1andSj+1(Ifj=n+1,thenSj+1=S0).However,fcan exponentially tend to infnity in the arbitrary two adjacent angular domains.

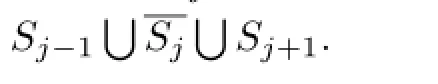
(iv) Iffexponentially tends to infnity in the adjacent angular domainsSj-1andSj,then for∀ε＞0,fhas infnitely many zeros in the angular domain{z:θj-ε≤argz≤θj+ε}and asr→∞,we have

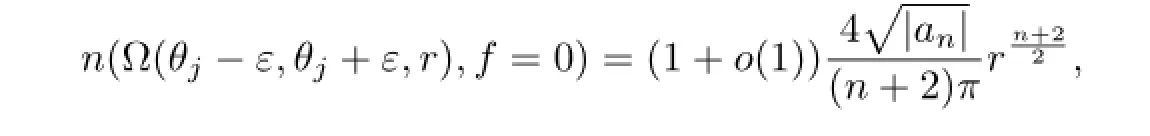
wheren(Ω(θ-ε,θ+ε,r),f=0)denotes the number of zeros off,counting multiplicities,in the sector Ω(θ-ε,θ+ε,r)={θ-ε≤argz≤θ+ε,0＜|z|≤r}.

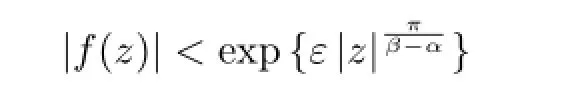
and forz∈C,we have|f(z)|≤M,then|f(z)|≤Mholds for allz∈D,whereM＞0 is a constant.

Lemma 2.5[13]Letf(z)be Fabry gap series,and for arbitrarily largeR,logM(R,f)＜Rλ, whereλ＞0 is a constant.Then for anyη1,η2∈(0,1),there exists a setE⊂(0,+∞)satisfngml(E∩[1,R])≥(1-η1)logR+o(1),such that for allr∈E,we have

Lemma 2.6[17]Letf(z),g(z)be two nonconstant meromorphic functions,then

Further,ifσ(g)＜σ(f),thenσ(fg)=σ(f+g)=σ(f).

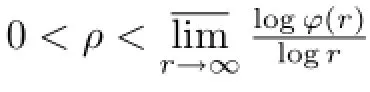
§3.Proofs of the Results

Proof of Theorem 1.1Letf(z)be a nonzero solution of Eq(1.1),by the basic theory of the complex diferential equations,we know thatf(z)is an entire function.

Firstly,we prove thatfcan not be a nonzero polynomial.

Suppose thatfis a nonzero polynomial solution of Eq(1.1).Rewrite Eq(1.1)in the form

This is a contradiction.Hence Eq(1.1)has no nonzero polynomial solution.

Secondly,we prove that every transcendental solutionfof Eq(1.1)has infnite order.

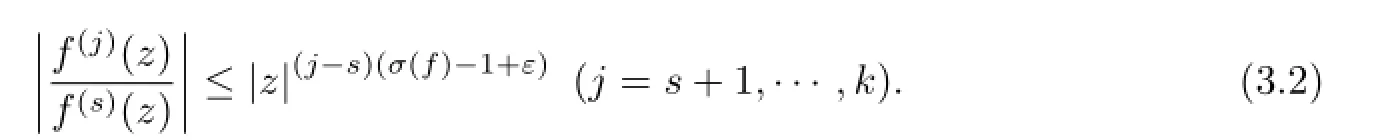
By Lemma 2.2,we know thatAs(z)has at mostn+2 zero cluster lines.Set

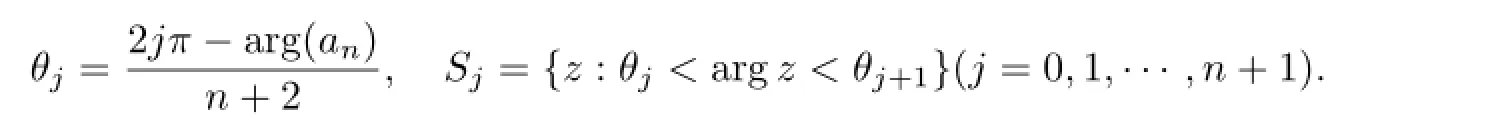
Now we discuss the following two cases.

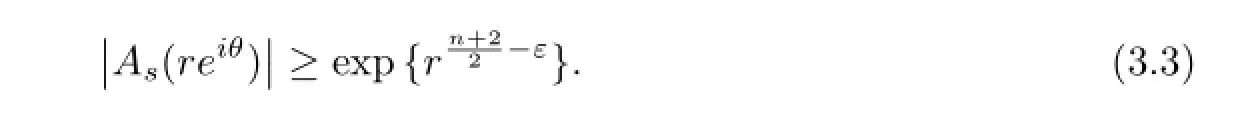
On the other hand,from the defnition of the growth order of entire function,we know that for the aboveε＞0,there existsr2＞0,such that for allzsatisfying|z|=r＞r2,we have

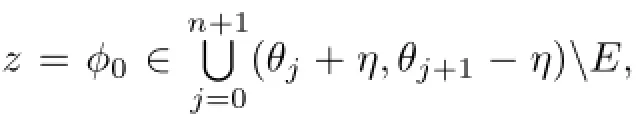
By(1.1)and(3.2)～(3.5),we get for sufciently largerm

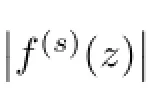
Letthen by(3.7)andfor sufciently larger,we get

Continuing the above step inductively,we obtain that

Sinceσ(f)＜+∞,for any givenδ(0＜δ＜η),there existsr1(δ)＞1,such that for allzsatisfying|z|=r≥r1(δ),we have

For each 0≤j≤n+1,take arbitrarilyqjdistinct pointsαjk∈(θj+η,θj+1-η)E(k= 1,2,···,qj)such that

Hence by(3.10),as|z|=r≥r1(δ),we have

Applying Lemma 2.4 tof(z)/zsin each domain

wherek=1,2,···,qj-1,Rjk=max{r1(δ),r(αjk),r(αj(k+1))},by(3.9)and(3.11),we obtain that

whereM=max{Mj:0≤j≤n+1}.

Hence by the above inequality and(3.12),applying Lemma 2.4 tof(z)/zsin each domain

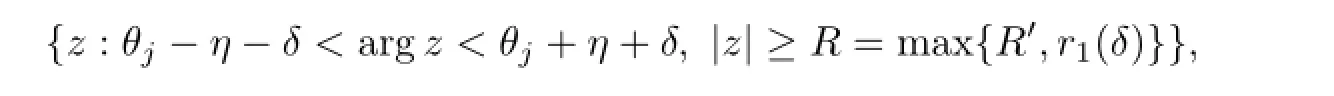
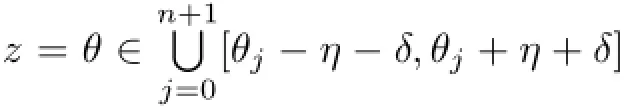
From the above argument,we obtain that|f(z)|≤M·|z|sholds for allzsatisfying|z|≥R. Thereforef(z)is a polynomial with degree no more thans.This contradicts thatf(z)is a transcendental entire function.Soσ(f)=+∞.

Case 2As(z)has less thann+2 zero cluster lines.Then by Lemma 2.2,we know that among thosen+2 angular domainsSj,there exists at least one angular domainSj0in whichAs(z)exponentially tends to zero.Hence for any givenη＞0 and eachthere existsr3(θ)＞0,such that for allzsatisfying argz=θand|z|=r＞r3(θ),we have

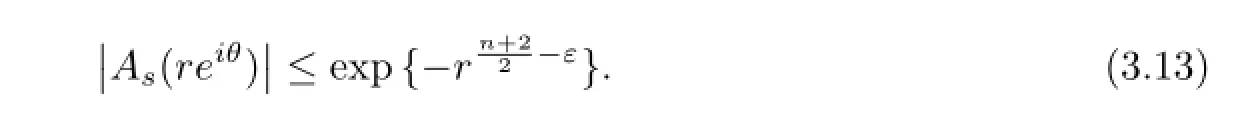
On the other hand,by 0＜σ(A0)≤1/2 and Lemma 2.4,we have

for allψ∈[0,2π)but at most one exceptionalψ0∈[0,2π).By(3.14),for any givenψ∈[0,2π)(ES{ψ0}),there exists an infnite sequence of points{zn=rneiψ},wherern→∞(n→∞),such that for sufciently largern,we have

So by(1.1),(3.2),(3.4),(3.13)and(3.15),for any argand sufciently largern,we have

whereM＞0,M′＞0 are constants,b=max{σ(Aj):j=1,···,k-1,j/=s}.This is impossible.Soσ(f)=+∞.Theorem 1.1 is thus completely proved.

Proof of Theorem 1.2We divided three cases to prove the result.

Case 1σ(As)＜σ(A0)=+∞.Suppose thatfis a nonzero solution of fnite order of Eq (1.1),by Lemma 2.6,we know that the order of the left side of(1.1)is infnite,and the order of the right side of(1.1)is zero.This is a contradiction.Therefore every nonzero solutionfof Eq(1.1)satisfesσ(f)=+∞.

Case 2σ(As)＜σ(A0)＜+∞.From the hypothesis of Theorem 1.2 and Theorem A,we know that every nonzero solutionfof Eq(1.1)satisfesσ(f)=+∞.

Case 3σ(As)＞σ(A0).Using the similar argument of Theorem 1.1,we know that every nonzero solution of Eq(1.1)is a transcendental entire function.Next we prove that every transcendental solutionfof Eq(1.1)is of infnite order.By Lemma 2.2,we know thatAs(z) has at mostn+2 zero cluster lines.Set

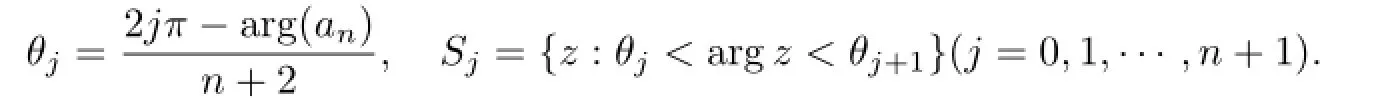
Now we discuss the following two subcases.

Subcase 3.1As(z)just hasn+2 zero cluster lines.Letf(z)be a transcendental solution of Eq(1.1),using the similar proof to that of case 1 in Theorem 1.1,we haveσ(f)=+∞.

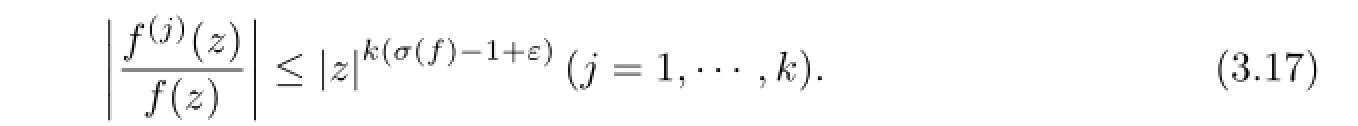
By Lemma 2.2,we know that among thosen+2 angular domainsSj,there exists at least one angular domainSj0in whichAs(z)exponentially tends to zero.Hence for any givenη＞0 andθ∈(θj0+η,θj0+1-η),there existsr0=r(θ)＞0,such that for allzsatisfying argz=θand|z|=r＞r0,we have

On the other hand,by Lemma 2.7,for the aboveε＞0,there exists a setE2⊂(0,∞)satisfying logdensE2=δ＞0,such that for|z|=r∈E2,we have

Sincewe have

Hence by(3.19)and(3.20),we obtain that there exists an infnite sequence of points{zn=satisfyingsuch that for sufciently largern,we have

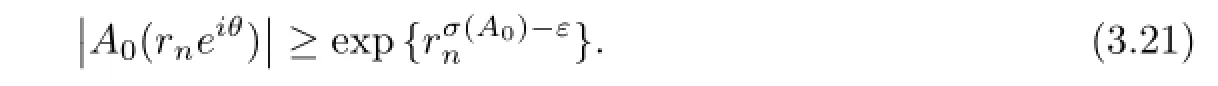
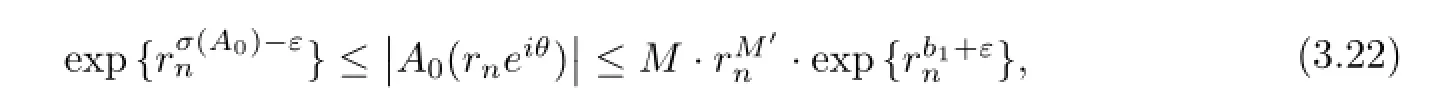
Hence by(1.1),(3.4),(3.17),(3.18)and(3.21),for any ray argwhenandrnis sufciently large,we havewhereM＞0,M′＞0 are constants,b1=max{σ(Aj):j=1,···,k-1,j/=s}.This is impossible.Soσ(f)=+∞.Theorem 1.2 is thus completely proved.

[1]YANG Le.Value Distribution Theory and New Research[M].Beijing:Science Press,1982.

[2]HAYMAN W.Meromorphic Functions[M].Oxford:Clarendon Press,1964.

[3]LAINE I.Nevanlinna Theory and Complex Diferential Equations[M].Berlin:W de Gruyter,1993.

[4]GUNDERSEN G,STEINBART E,WANG S.The possible orders of solutions of linear diferential equations with polynomial coefcients[J].Trans Amer Math Soc,1998,350(3):1225-1247.

[5]CHEN Zong-xuan,YANG Chung-chun.Quantitative estimations on the zeros and growths of entire solutions of linear diferential equations[J].Complex Variables Theory Appl,2000,42(2):119-133.

[6]HELLERSTEIN S,MILES J,ROSSI J.On the growth of solutions of certain linear diferential equations[J]. Anna Acad Sci Fenn,1992,17A(2):343-365.

[7]GUNDERSEN G.Finite order solutions of second order linear diferential equations[J].Trans Amer Math Soc,1988,305:415-429.

[8]CHEN Zong-xuan.The growth of solutions off′′+e-zf′+Q(z)f=0 where the orderσ(Q(z))=1[J]. Sicence in China,2002,45A:209-300.

[9]WU Peng-cheng,ZHU Jun.On the growth of solutions to the complex diferential equationf′′+Af′+Bf= 0[J].Science in China,Mathematics,2011,54:939-947.

[10]MAO Zhi-qiang,LIU Hui-fang.On the growth of a class of higher order linear diferential equations with meromorphic coefcients[J].Chin Quart J of Math,2009,24(2):278-283.

[11]WU Xiu-bi,WU Peng-cheng.On the growth of solutions off′′+Af′+Bf=0,whereAis a solution of a second order linear diferential equation[J].Acta Math Sci,2013,33A(1):46-52.

[12]ZHANG Shi-mei,WU Peng-cheng,HU Guang-ming.On the growth of solutions of some higher order linear diferential equations[J].Journal of Guizhou Normal University(Natural Sciences),2013,31(3):46-49.

[13]SONS L R.An analogue of a theorem of W.H.J.Fuchs on gap series[J].Proc London Math Soc,1970,21(3): 525-539.

[14]GUNDERSEN G.Estimates for the logarithmic derivative of a meromorphic function,plus similar estimates[J].J London Math Soc,1988,37(2):88-104.

[15]HILLE E.Lectures on Ordinary Diferential Equations[M].Ontario:Addison Wesley Publishing Company, 1969.

[16]TITCHMARSH E C.The Theory of Functions[M].London:Oxford Univ Press,1986.

[17]YI Hong-xun,YANG Chung-chun.Uniqueness Theory of Meromorphic Functions[M].New York:Kluwer Academic Publishers,2003.

[18]ISHIZAKI K,TOHGE K.On the complex oscillation of some linear diferential equations[J].J Math Anal Appl,1997,206:503-517.

O174.52

:A

1002–0462(2016)04–0369–10

Received date:2014-07-08

Foundation item:Supported by the National Natural Science Foundation of China(11201195);Supported by the Natural Science Foundation of Jiangxi Province(20122BAB201012,20132BAB201008)

Biographies:XIONG Hui(1989-),male,native of Nanchang,Jiangxi,M.S.D.,engages in complex analysis; LIU Hui-fang(1973-),female,native of Fengcheng,Jiangxi,a professor of Jiangxi Normal University,Ph.D., engages in complex analysis.

2000 MR Subject Classifcation:30D35,34A20