Some Inequalities for the Lp-polar Curvature Images of Star Bodies

(1.College of Mathematics and Statistics,Northwest Normal University,Lanzhou730070,China;2.College of Mathematics and Statistics,Hexi University,Zhangye734000,China)

Some Inequalities for the Lp-polar Curvature Images of Star Bodies

LI Xin-hong1,MA Tong-yi2

(1.College of Mathematics and Statistics,Northwest Normal University,Lanzhou730070,China;2.College of Mathematics and Statistics,Hexi University,Zhangye734000,China)

Zhu,L¨u and Leng extended the concept ofLp-polar curvature image.We continuously study theLp-polar curvature image and mainly expound the relations between the volumes of star bodies and theirLp-polar curvature images in this article.We frst establish theLp-afne isoperimetric inequality associated withLp-polar curvature image.Secondly, we give a monotonic property forLp-polar curvature image.Finally,we obtain an interesting equation related toLp-projection body ofLp-polar curvature image andLp-centroid body.

star bodies;convex bodies;Lp-curvature image;Lp-polar curvature image

§1.Introduction

LetKndenote the set of convex bodies(compact,convex subsets with non-empty interiors)in Euclidean space Rn,writeandthe set of convex bodies containing origin in their interiors and the set of origin-symmetric convex bodies in Rn,respectively.Useto denote the class of star bodies(about the origin)in Rnandto denote the class of star bodies(about the origin) which are symmetric about origin.Denote byV(·)then-dimensional volume function,for the standard unit ballBin Rn,noteV(B)=ωn,here

The Minkowski problem dealing with existence,uniqueness,regularity and stability of closed convex hypersurfaces whose Guass curvature(as a functional of the outer normals)is preassigned.Further,a generalization of the Minkowski problem is known as theLp-Minkowskiproblem(see[1])and many beautiful conclusions to this problem were made in[2-7].Lutwak showed the concept ofLp-curvature image.Ifthen theLp-curvature image, ΛpK,ofKwhose radial function is defned by(see[2])

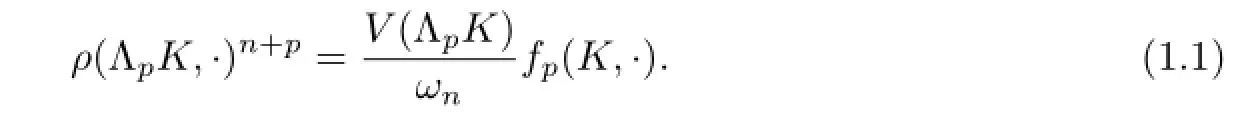
Herefp(K,·)is theLp-curvature image ofKand its defnition as follows.ForK∈Kn,we say it has a curvature function(see[2])f(K,·):Sn-1-→R whose surface area measureS(K,·)is absolutely continuous associated with spherical Lebesgue measureSand

Forwe say it has aLp-curvature function(see[2])if itsLpsurface area measure is absolutely continuous associated with spherical Lebesgue measureSand

Denote byFn,andthe set of all bodies inKn,andrespectively,and all of them have a positive continuous curvature function.

As the application forLp-curvature image,Lutwak proved the followingLp-afne isoperimetric inequality ofLp-curvature image.

Theorem A(see[2])Ifthen

with equality if and only ifKis an ellipsoid.

A weak solution to the evenLp-Minkowski problem was given for alln/=p≥1.Ifµis an even positive Borel measure on unit sphereSn-1which is not concentrated on a great sphere ofSn-1,then there exists an unique origin-symmetric convex bodyL,such thatSp(K,·)=µ(see [1]).Hence,given a continuous functionf:such thatf(·)is an even positive Borel measure onthere exists a bodysuch that

By(1.4),ifandp≥1,then theLp-polar curvature image,ofK(see[8])

Specially,for the casep=1,it is just the classical polar curvature image,note(see[2]).

Zhu[9]studied theLp-polar curvature images of star bodies and drew some conclusions associated withLp-afne surface area andLp-mixed afne surface area.

In this article,we mainly give the relations between the volumes of star bodies and theirLppolar curvature images.Firstly,we establish theLp-afne isoperimetric inequality ofLp-polar curvature image as follows.

Theorem 1.1Ifthen

with equality if and only ifKis an ellipsoid.

Similarly,we also establish the following inequality.

Theorem 1.2Ifthen

with equality forp＞1 if and only ifK∗andare dilates,forp=1 if and only ifK∗andare homothetic.

Secondly,we give a monotonic property ofLp-polar curvature image as follows.

Theorem 1.3IfandK⊆L,then

with equality forn=pif and only ifK=L;forn/=p=1 if and only if ΛKand ΛLare translation;forn/=p＞1 if and only ifK=L.

Finally,we obtain an interesting equation for theLp-projection body ofLp-polar curvature imagesand theLp-centroid body ofKas follows.

Theorem 1.4Ifandp≥1,then

It’s easy to get the well knownLp-Busemann-Petty centroid inequality(see Section 3).

The defnitions and notations associated with the above research contents will be introduced in Section 2.

§2.The Brunn-Minkowski-Firey Theory

2.1The Support Funciton,the Radial Function and the Polar of Convex Body

A function,h(K,·):Rn-→R is said to be the support function ofK(see[10-11]),provided that wheneverK∈Kn,

herex·ydenotes the standard inner product ofxandy.

In[10],by the defnition of support function forµ＞0,there is

A function,ρ(K,·):Rn{0}-→[0,+∞)is said to be the radial function ofK(see[10-11]), provided that wheneverKis a compact star-shaped(about origin)in Rn,is defned by

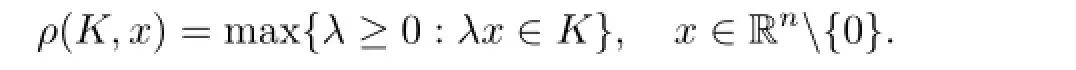
Kwill be called a star body(about origin)wheneverρ(K,·)is positive and continuous.And for allu∈Sn-1,two star bodiesKandLare said to be dilates(of one another)ifρ(K,u)/ρ(L,u) is independent ofu.

In[12],by the defnition of radial function forµ＞0,there is

ForK∈Kno,the polar body ofK,K∗,is defned by(see[10-11])

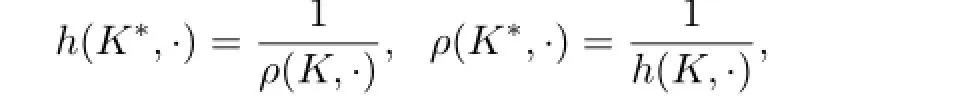
for allForand its polar body,the Blaschke-Stantal´o inequality was introduced in[10-11].Ifthen

From this,the support and radial functions ofK∗are defned by(see[10-11])

with equality if and only ifKis an ellipsoid.

2.2Lp-mixed Volume andLp-dual Mixed Volume

LetK,L∈Kn,α,β＞0 and forp≥1,theLp-Minkowski combination ofKandLis defned by Firey[13]

Lutwak[1]extended the concept ofLp-mixed volumeVp(K,L).Let0,then forp≥1,theLp-mixed volume,Vp(K,L),ofKandLdefned as

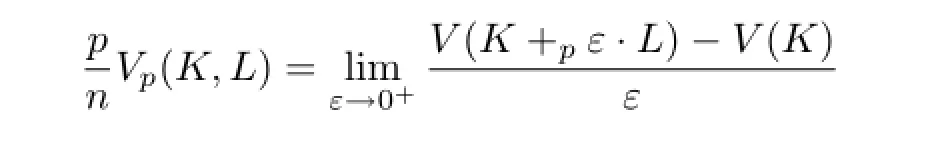
and for any1,there exists a regular Borel measureSp(K,·)onsuch that theLp-mixed volumeVp(K,L)has the following integral representation

It turns out that the measureSp(K,·)is absolutely continuous associated withS(K,·)and has (see[2])

From(1.3),theLp-mixed volumeVp(K,L)can be rewritten that for

for allLetL=Kin(2.6),then

The Minkowski inequality forLp-mixed volumes as follows(see[2])

with equality forp=1 if and only ifKandLare homothetic;forp＞1 if and only ifKandLare dilates.

From(2.8),it has an immediate consequence as follows.

Lemma 2.1If=p≥1 and

thenK=L.Ifp=n,it does not imply thatK=L,but only thatKandLare dilates.

Next,we introduce the concept ofLp-dual mixed volumes

For everytheLp-dual mixed volumeshas the following integral representation(see[2])

The Minkowski inequality forLp-dual mixed volumes as follows(see[2])

with equality if and only ifKandLare dilates.

From(2.10),it has an immediate consequence as follows.

Lemma 2.2(see[12])Ifthen for all

2.3Lp-afne Surface Area

Forp≥1,theLp-afne surface area,Ωp(K),ofis defned by Lutwak[2]

Together with(1.1)and(2.11),Lutwak proved thatfor1.

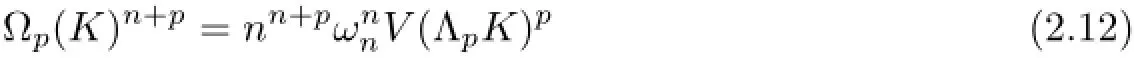
Similarly,from(1.5)and(2.11),Zhu,L¨u and Leng[8]proved that for1,

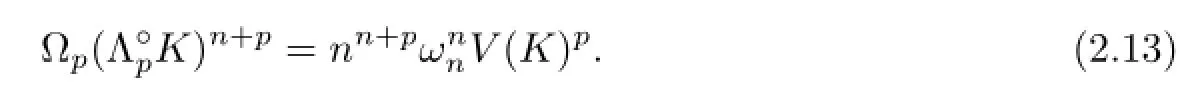
2.4Lp-projection Body andLp-centriod Body

The notion ofLp-projection body was posed by Lutwak(see[14]).For1,theLp-projection body,ΠpK,ofKis an origin-symmetric convex body whose support function is defned by

for allu∈Sn-1.Here

As the application of theLp-projection body,it has a consequence in[15]as follows.For1,then

with equality if and only ifKis an ellipsoid centered at the origin.

Then we combine(2.13)with(2.15)to get

Lutwak and Zhang[16]introduced the notion ofLp-centroid body.IfKis a compact starshaped body about the origin andp≥1,then for allu∈Sn-1,theLp-centroid body,ΓpK,ofKis the origin-symmetric convex body whose support function is defned by

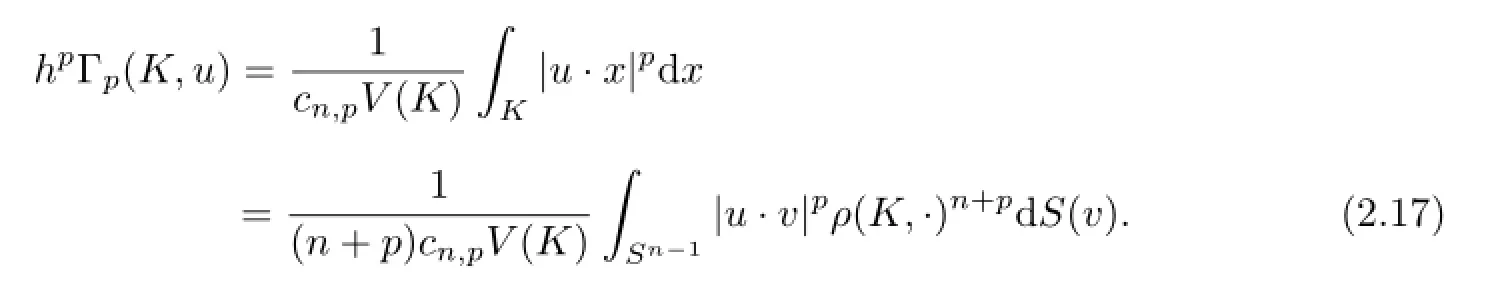
§3.The Proofs of Main Results

In the section,we shall complete the proofs of theorems 1.1～1.4.In order to prove the Theorem 1.1,we need the following lemmas.

Lemma 3.1(see[8])Ifn/=p＞1 andthen

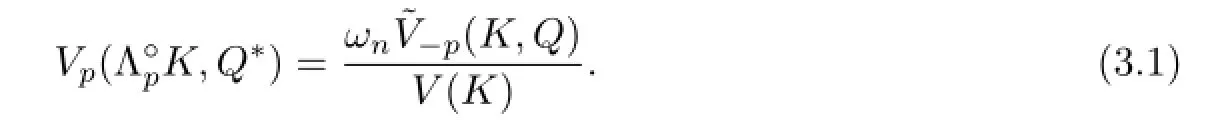
Lemma 3.2Ifthen forφ∈SL(n),

whereφ-tis the inverse transformation of transposition ofφ.

ProofAccording to the invariance of theLp-dual mixed volume,under simultaneous unimodular centro-afne transformations as follows(see[14]).Letandp≥1,then forφ∈SL(n),

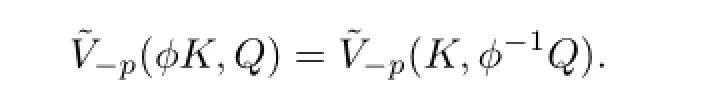
Putting(3.1)into the above formula,we get

By the invariance of theLp-mixed volume,Vp,under simultaneous unimodular centro-afne transformations,it follows that

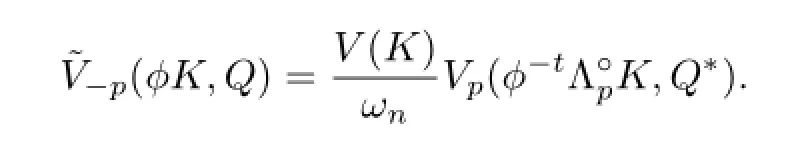
Together with(3.1),then

Applying Lemma 2.1.we get the equation(3.2)forn/=p＞1.

Lemma 3.3(see[8])Suppose1 andthenK=L.

Proof of Theorem 1.1Letin(3.1),combining(2.7)and(2.10),we have

with equality if and only ifKandare dilates.

Together with the Blaschke-Stantal´o inequality(2.3),it follows that

with equality if and only ifis an ellipsoid.

By defnition(1.5),we know thatfor the unit ballForφ∈SL(n)andone hasThen together with(3.2),it shows that,ifEis a centered ellipsoid,such thatV(E)=ωn,then

Applying Lemma 3.3,we know that forandp＞1,the bodyis a centered ellipsoid if and only ifKis a centered ellipsoid.Together with the equality conditions in(3.3)and(3.4), we get equality in(1.6)if and only ifKis an ellipsoid.

Proof of Theorem 1.2LetQ=Kin(3.1),combining(2.7)and(2.8),we have

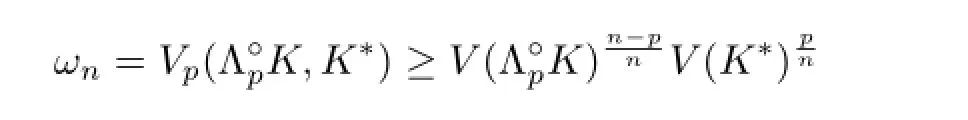
and this is just inequality(1.7),with equality forp=1 if and only ifandK∗are homothetic;forp＞1 if and only ifandK∗are dilates.

In order to prove Theorem 1.3,we need the following lemma.

Lemma 3.4If1 and the constantc＞0,then

ProofSince for constantλ＞0,there is a factV(λQ)=λnV(Q)for allQ∈φno.Then putting(2.2)into(1.5),we get

for constantc＞0.This together with(1.3)and(2.5),we know that

which can be rewritten as follows byand(2.1),

Then from(2.4),we get

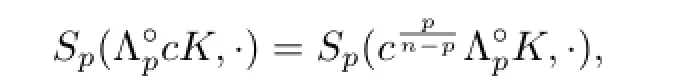
which implies equality(3.5).

Proof of Theorem 1.3Together withK⊆Land(2.9),we get that for all

with equality if and only ifK=Lby Lemma 2.2.Putting(3.1)into(3.6),it follows that

for allLettogether with(2.7)andLp-Minkowski inequality(2.8),we have

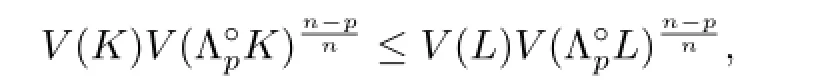
which yields(1.8).

Now we discuss the conditions of equality holds in inequality(1.8).

For the casen=p,we easily see that equality holds in inequality(1.8)if and only ifK=L.

For the casen/=p=1,we may takeSince the mappingis bijective,thenis the inverse ofThus,together withK=Landwe have

According toS1(x+ΛK,·)=S(x+ΛK,·)=S(ΛK,·),it can be seen thatf1(x+ΛK,·)=f(ΛK,·)by(1.2).Together with(2.11),we get Ω(x+ΛK)=Ω(ΛK)and then by(2.12)and (2.13)to getV(Λ1(x+ΛK))=V(K).Thus,combining(1.5)and(1.1),we obtain

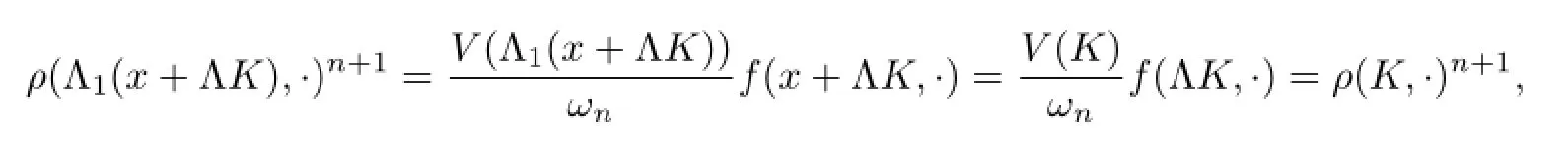
i.e.,

This together with(3.5),then the equation(3.7)can be rewritten as follows

and this impliesc=1,that is,ΛL=x+ΛKforn＞1.Hence,we see that equality holds in inequality(1.8)forn/=p=1 if and only if ΛKand ΛLare translation.

Forn/=p＞1,we may supposeand together with(3.5)to getThen byK=Land Lemma 3.3,it follows thatThis meansprovided thatn/=p＞1.Again with Lemma 3.3,we know that for the casen/=p＞1,the equality holds in inequality(1.8)if and only ifK=L.

To sum up,the equality holds in inequality(1.8)forn=pif and only ifK=L;forn/=p=1 if and only if ΛKand ΛLare translation;forn/=p＞1 if and only ifK=L.

Proof of Theorem 1.4Combining(2.14),(1.3),(1.5)and(2.17),we see that for allu∈Sn-1,

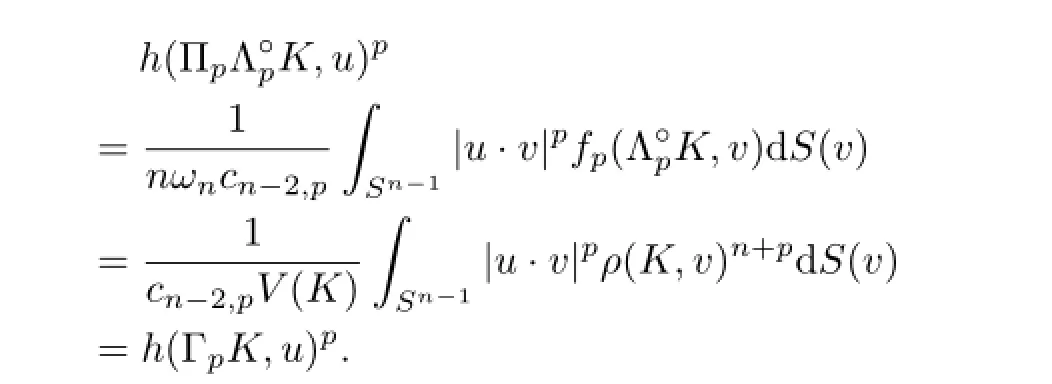
From this,we immediately obtain(1.9).

Finally,according to(1.9)and inequality(2.16),we immediately obtain the well knownLp-Busemann-Petty centroid inequality(see[14])

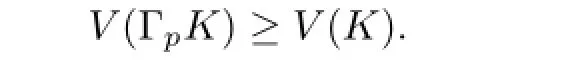
[References]

[1]LUTWAK E.The Brunn-Minkowski-Firey theory I:Mixed volumes and the Minkowski problem[J].Journal of Diferential Geommetry,1993,38(1):131-150.

[2]LUTWAK E.The Brunn-Minkowski-Firey theory II:Afne and geominimal surface areas[J].Advances in Mathematics,1996,118(2):244-294.

[3]LUTWAK E,OLIKER V.On the regularity of solutions to a generalization of the Minkowski problem[J]. Journal of Diferential Geommetry,1995,41(3):227-246.

[4]LUTWAK E,YANG D,ZHANG Gao-yong.On theLp-Minkowski problem[J].Transactions of American Mathematical Society,2003,356(11):4359-4370.

[5]STANCU A.The discrete planarL0-Minkowski problem[J].Advances in Mathematics,2002,167(1):160-174.

[6]STANCU A.On the number of solutions to the descrete two-dimensionalL0-Minkowski problem[J].Advances in Mathematics,2003,180(1):290-323.

[7]UMANSKIY V.On solvability of the two-dimensionalLp-Minkowski problem[J].Advances in Mathematics, 2003,180(1):176-186.

[8]ZHU Xian-yang,L¨U Song-jun,LENG Gang-song.Extended afne surface area and zonotopes[J].Bol Soc Mat Mexicana,2008,14(3):125-138.

[9]ZHU Xian-yang.Some inequalities forLp-mixed afne surface area[J].Chinese Quarterly Journal of Mathematics,2012,27(4):572-581.

[10]SCHNEIDER R.Convex Bodies:The Brunn-Minkowski Theory[M].Cambridge:Cambridge University Press,1993.

[11]GARDNER R J.Geometric Tomography[M].Cambridge:Cambridge University Press,1995.

[12]WANG Wei-dong,WEI Dai-jun,XIANG Yu.Some inequalities for theLp-curvature image[J].Journal of Inequalities Applications,2009,6:1-12.

[13]FIREY W J.p-means of convex bodies[J].Mathematica Scandinavica,1962,10(1):17-24.

[14]LUTWAK E,YANG D,ZHANG Gao-yong.Lp-afne isopermetric inequalities[J].Journal of Diferential Geommetry,2000,56(1):111-132.

[15]WANG Wei-dong.Extremum Problem in Convex Bodies Geometry ofL-pspace[D].Shanghai:Shanghai University,2006.

[16]LUTWAK E,YANG D,ZHANG Gao-yong.Blaschke-Santal´o inequalities[J].Journal of Diferential Geommetry,1997,47(1):1-16.

O184

:A

1002–0462(2016)04–0349–10

Received date:2014-05-30

Foundation item:Supported by the National Natural Science Foundation of China(11161019)

Biographies:LI Xin-hong(1986-),female,native of Lanzhou,Gansu,a postgradute of Northwest Normal University,engages in convex geometric analysis and geometric inequality theory;MA Tong-yi(1959-),male, native of Huining,Gansu,a professor of Hexi University,M.S.D.,engages convex geometric analysis,distance geometry,discrete geometry and inequality theory.

2000 MR Subject Classifcation:52A40,52A20