Certain Subclasses of Analytic Functions Involving the Generalized Dziok-Srivastava Operator

(School of Mathematics and Statistics,Chifeng University,Chifeng024000,China)

Certain Subclasses of Analytic Functions Involving the Generalized Dziok-Srivastava Operator

LI Shu-hai,TANG Huo,MA Li-na

(School of Mathematics and Statistics,Chifeng University,Chifeng024000,China)

The generalized Dziok-Srivastava operator is used here to introduce a class of analytic functions in the open unit disc.We provide convolution properties,some subordination relations and the problem of radius.The results presented here extend some of the earlier results.

multivalent functions;Dziok-Srivastava operator;convolution properties;subordination relations

§1.Introduction

LetApdenote the class of functions of the form

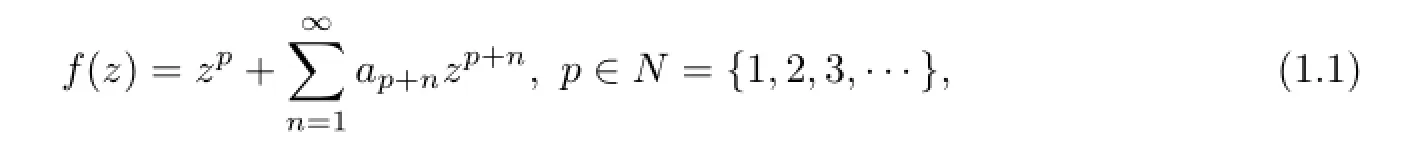
which are analytic andp-valent in the open unit disc U={z∈C:|z|＜1}.In particular,we letA1=A.

Received date:2014-07-16

Foundation item:Supported by the Natural Science Foundation of Inner Mongolia of China(2014MS0101); Supported by the Natural Science Foundation of China(11561001);Supported by the Higher School Research Foundation of Inner Mongolia of China(NJZY16251)

Biographies:LI Shu-hai(1966-),male(mongolian),native of Chifeng,Inner Mongolia,a professor of Chifeng College,engages in geometric function theory and applications;TANG Huo(1979-),male,native of Anqin,Anhui, an associate professor of Chifeng College,engages in complex analysis;MA Li-na(1982-),female(mongolian), native of Chifeng,Inner Mongolia,a lecturer of Chifeng College,engages in harmonic analysis and complex analysis.

Letf(z),g(z)∈Ap,wheref(z)is given by(1.1)andg(z)is defned by

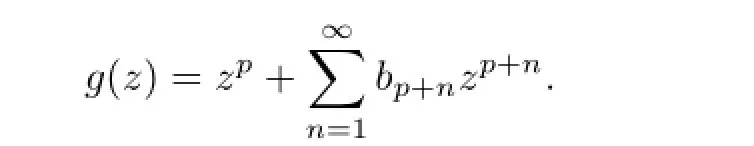
The Hadamard product(or convolution)(f∗g)(z)of the functionsf(z)andg(z)is defned by

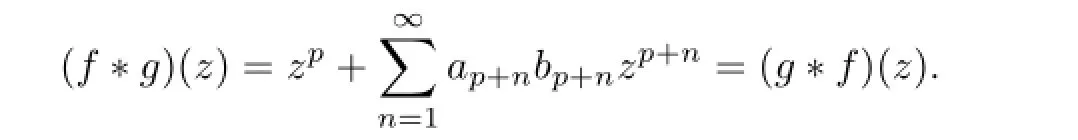
For two functionsf1andf2,analytic in U,we say that the functionf1is subordinate tof2in U and write

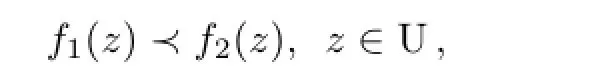
if there exists a Schwarz functionω,which is analytic in U with

such that

Furthermore,if the functionf2is univalent in U,then we have the following equivalence:

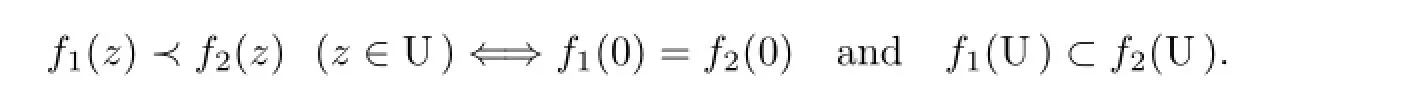
A functionp(z),analytic in U withp(0)=1 is said to be in the classP(A,B;ρ,δ)(-1≤B＜A≤1,0≤ρ＜1,0≤δ＜1)if and only if

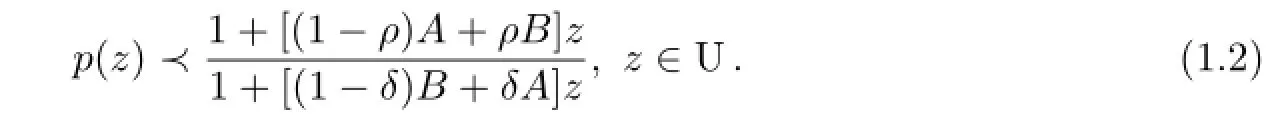
By the defnition of subordination,the condition(1.2)is equivalent to

that is,

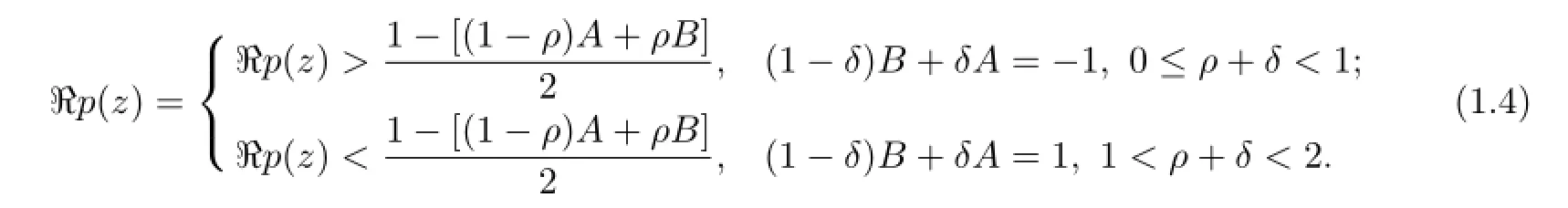
Remark 1.1Forδ=0,P(A,B;ρ,0)=P(A,B,ρ),the class introduced by Arif et al[1]. Forρ=0,δ=0,P(A,B;0,0)=P(A,B),the well-known class introduced by Janowski[2].Forρ=0,δ=0,A=1,B=-1,we obtain the well-known classPof functions with positive real part.

Now,we defne two subclassesSp[A,B,ρ,δ]andKp[A,B,ρ,δ]of the classApfor-1≤B＜A≤1,0≤ρ＜1,0≤δ＜1 andp∈Nas follows

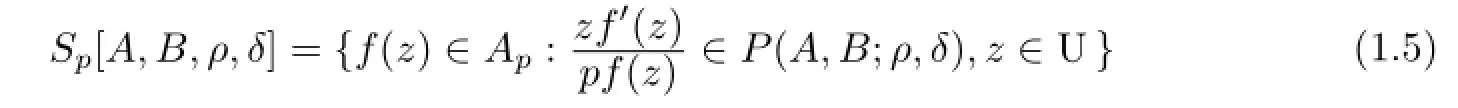
and

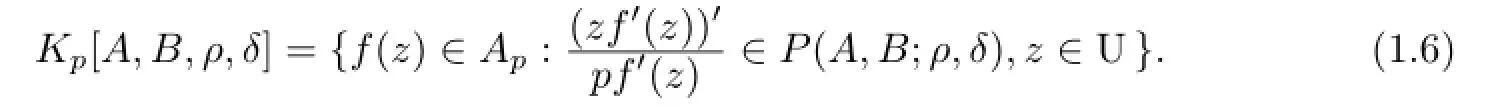
Clearly,

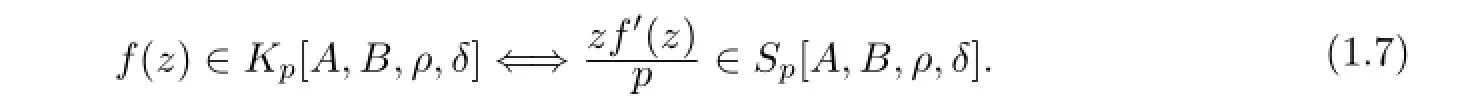
We note that the classandwhereandK1[A,B,ρ]are the classes studied by Polato˜glu et al in[3].Also,

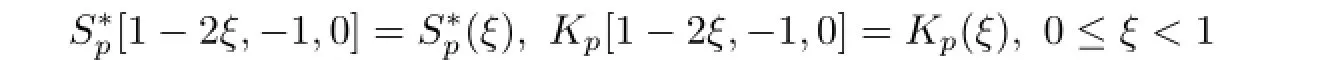
and

For parametersαj∈C(j=1,···,l)andthe generalized hypergeometric functionlFm(z)is defned by

wherel≤m+1,l,m∈N0=N∪{0},z∈U,

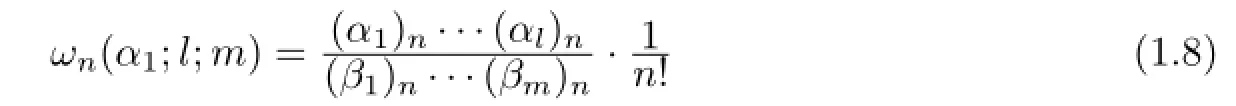
and(a)nis the Pochhammer symbol defned(in terms of the Gamma function)by

Dziok and Srivastava[4]introduced a linear operatorHp(α1,···,αl;β1,···,βm):Ap→Ap:

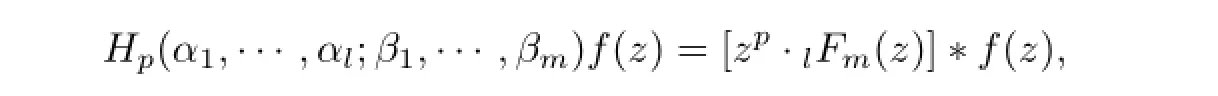
wherel≤m+1,l,m∈N0=N∪{0},z∈U.

Iff(z)∈Apis given by(1.1),then we have

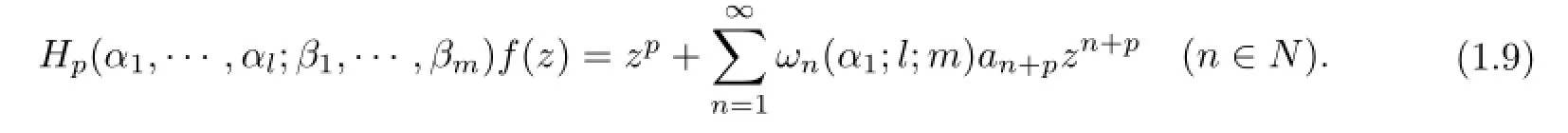
In order to make the notation simple,we write

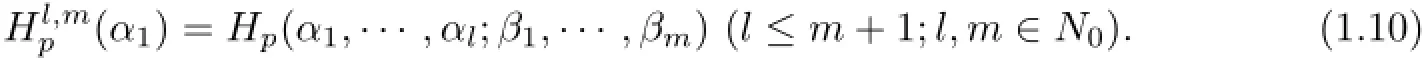
In this paper,we defned the linear operatoras follows

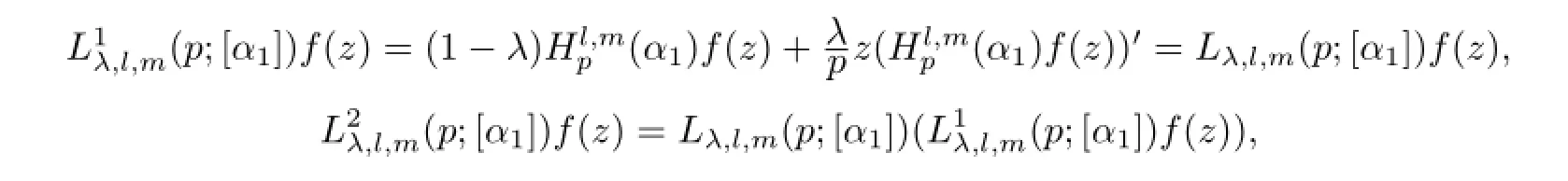
in general,

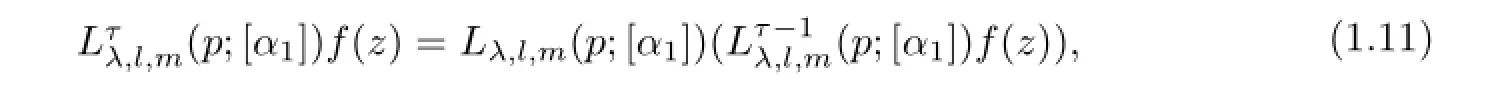
whereλ≥0,l≤m+1,m∈N0,τ∈N.

If the functionf(z)is given by(1.1),then we see from(1.10)and(1.11),we obtain

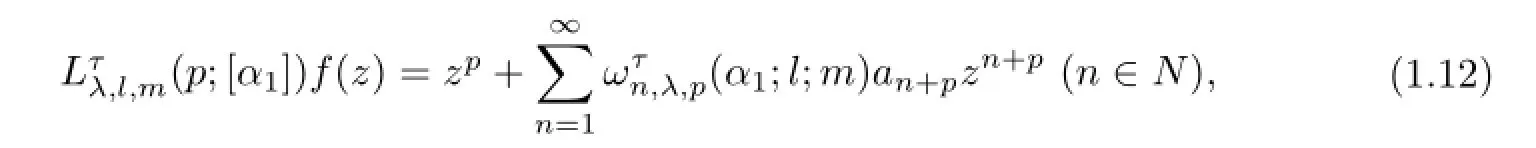
where

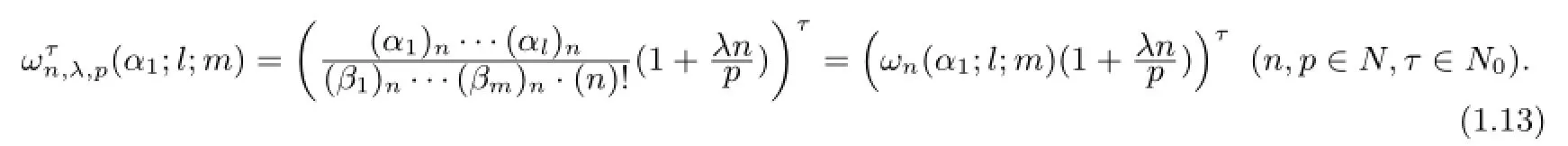
Remark 1.2Settingτ=1,λ=0,the linear operator,leads immediately to the Dziok-Srivastava linear operator[4](see also[5]),which contains,as note that whenp=1 the linear operatorwould reduce to the familiar Srivastava et al.linear operator [6].Note that whenl=1,m=0,λ=1 andα1=1 the linear operatorwould reduce to the familiar Eker et al[7]linear operator,includes(as its special cases)various other linear operator introduced and studied by Carlson and Shafer[8],Owa[9],Ruscheweyh[10]and Sˇalˇagean[11].

Next,using the operatorwe introduce the following classes of analytic functions forp∈N,0≤ρ＜1,0≤δ＜1,-1≤B＜A≤1,l≤m+1 andτ,l,m∈N0=N∪{0}

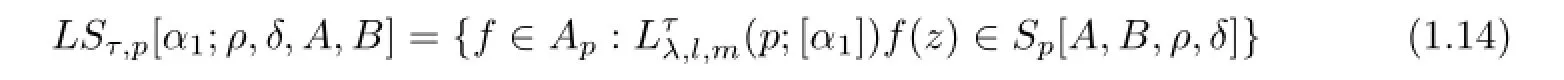
and

We also note that

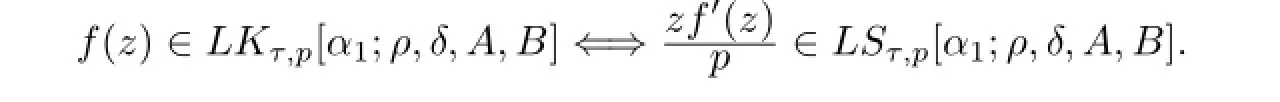
§2.Convolution Properties

Theorem 2.1The functionfof the form(1.1)is in the classSp[A,B,ρ,δ]if and only if

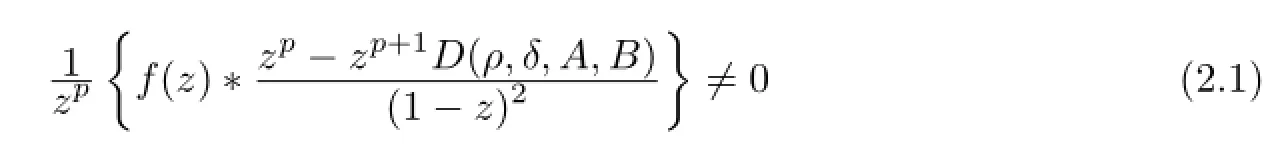
for allz∈U,0≤θ＜2π,0≤ρ＜1,0≤δ＜1 andρ+δ/=1,where

ProofFirst,supposefis in the classThen from(1.5),we get

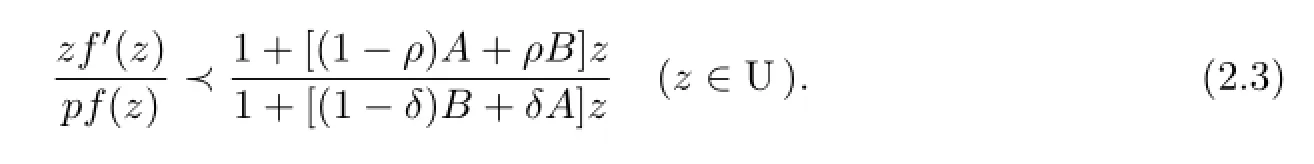
According to the relationship of subordination,there exists a functionω(z)analytic in U withω(0)=0 and|ω(z)|＜1,such that

which is equivalent to

Since

we obtain

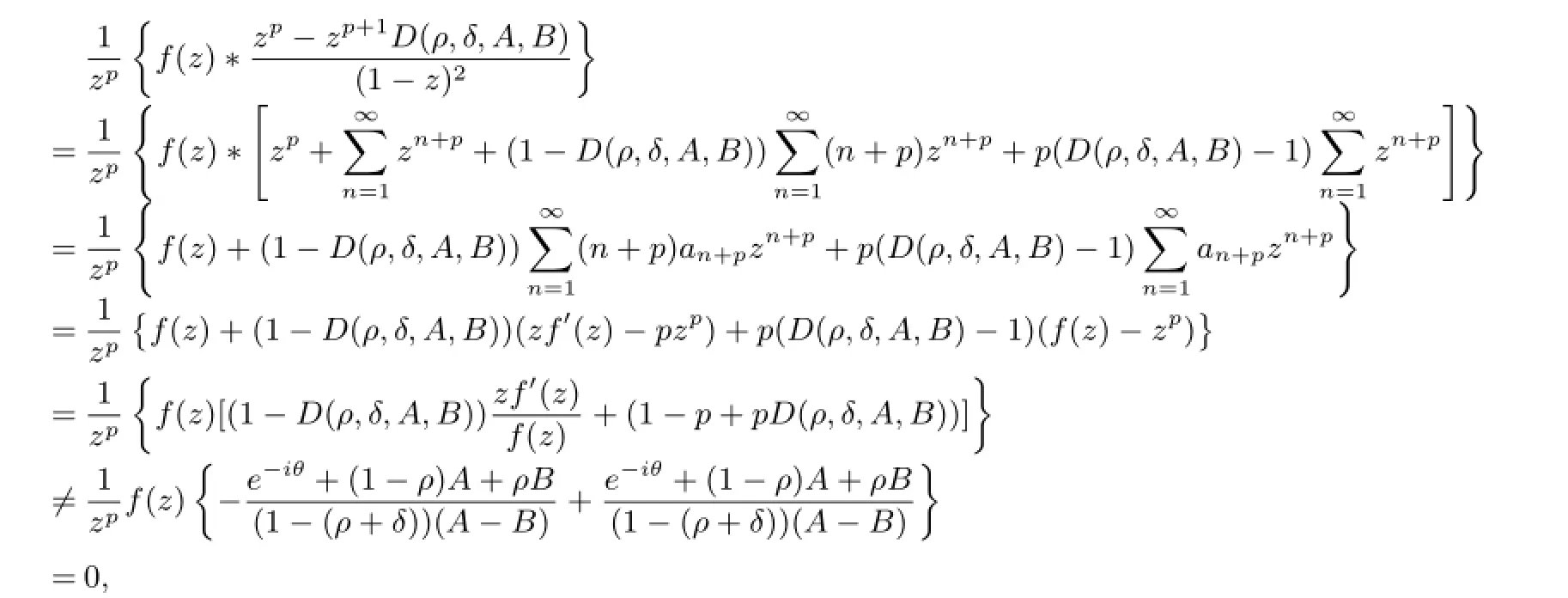
which proves the necessary part.

Again,if the condition(2.1)holds then because

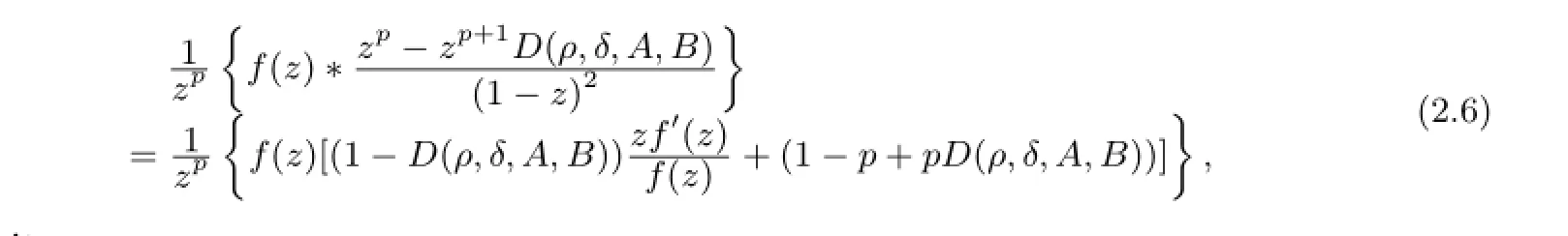
we can write

Then we easily obtain the required result as

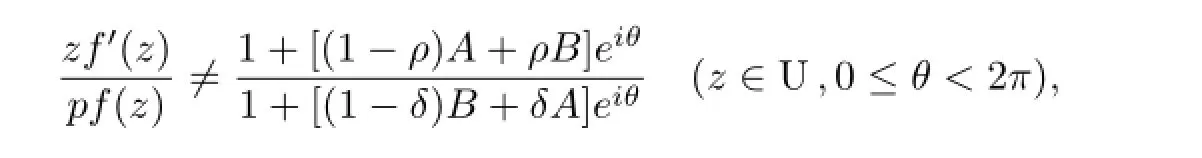
which proves thatf(z)∈Sp[A,B,ρ,δ].

Using(1.7)and Theorem 2.1,we have

Theorem 2.2The functionfof the form(1.1)is in the classKp[A,B,ρ,δ]if and only if

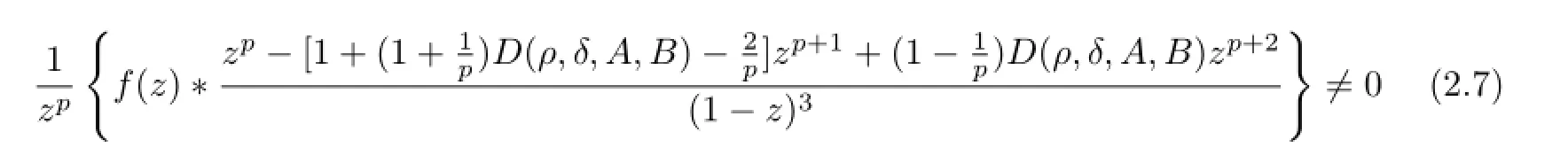
for allz∈U,0≤θ＜2π,0≤ρ＜1,0≤δ＜1 andρ+δ/=1,whereD(ρ,δ,A,B)is given by (2.2).

Remark 2.1Settingρ=δ=0 in Theorem 2.1 and Theorem 2.2,respectively,we obtain the known results by Sarkar et al[12](theorems 2.1～2.2).Also,settingρ=δ=0 andp=1 in Theorem 2.1 and Theorem 2.2,respectively,we obtain the known results by Aouf and Seoudy[13](theorems 1～2).

Using(1.12),(2.6)and Theorem 2.1,we have

Theorem 2.3Let 0≤ρ＜1,0≤δ＜1 andρ+δ/=1.If the functionfof the form(1.1).Then a necessary and sufcient condition for the functionfto be in the classLSτ,p[α1;ρ,δ,A,B]is that

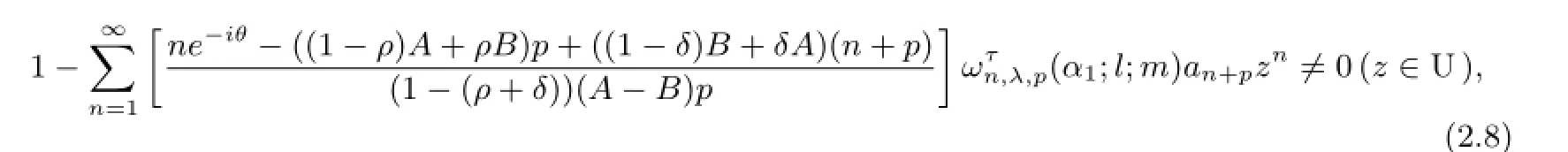
where 0≤θ＜2πandis given by(1.13).

Corollary 2.1Let 0≤ρ＜1,0≤δ＜1 andρ+δ/=1.If the functionfof the form (1.1)is in the classLSτ,p[α1;ρ,δ,A,B],then

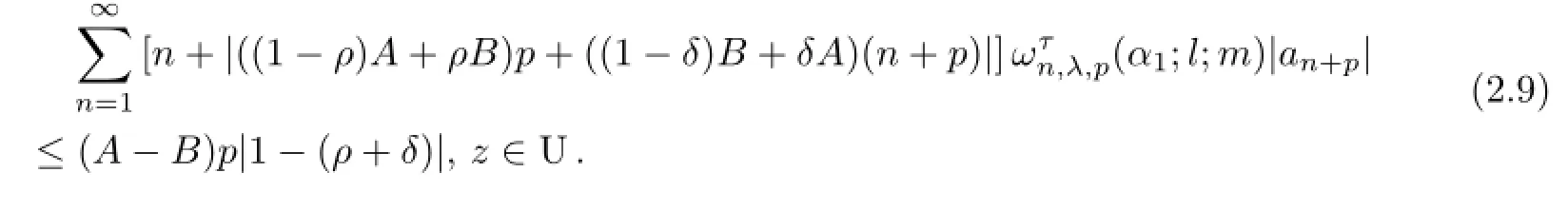
Using(1.16)and Theorem 2.2 we have

Theorem 2.4Let 0≤ρ＜1,0≤δ＜1 andρ+δ/=1.If the functionfof the form(1.1).Then a necessary and sufcient condition for the functionfto be in the classLKτ,p[α1;ρ,δ,A,B]is that

where 0≤θ＜2πandis given by(1.13).

Also,we can use the same method of Corollary 2.1 to prove the following corollary.

Corollary 2.2Let 0≤ρ＜1,0≤δ＜1 andρ+δ/=1.If the functionfis defned by (1.1)andf∈LKτ,p[α1;ρ,δ,A,B],then

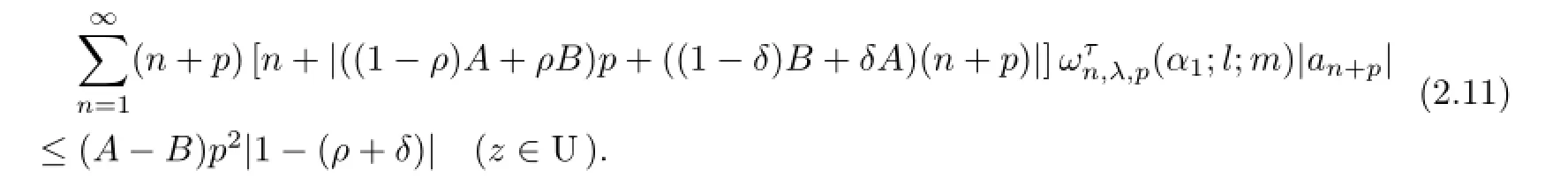
§3.Subordination Relations

To prove our results,we will need the following lemma.

Lemma 3.1[14-15]Letgbe univalent in U and letφandψbe analytic in a domainEcontainingg(U),withψ(ω)/=0 whenω∈g(U).Set

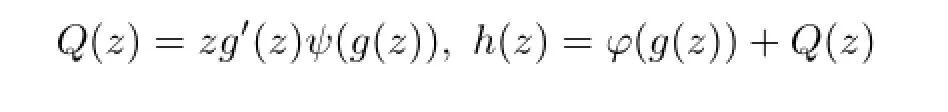
and suppose that

(i)Qis univalent and starlike in U and

Ifpis analytic in U,withp(0)=g(0),p(U)⊂Eand

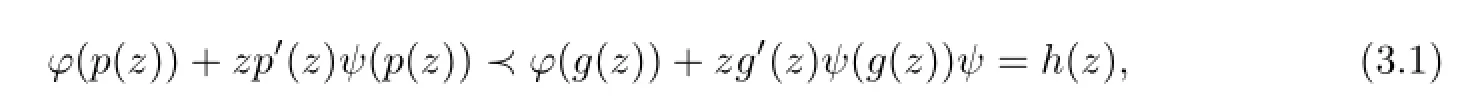
thenp≺gandgis the best dominant of the subordination(3.1).

Note that the univalent functiong(z)is said to be a dominant of the diferential subordination(3.1)ifp(z)≺g(z)for allp(z)satisfying(3.1).If˜g(z)is a dominant of(3.1)and for all dominantsg(z)of(3.1),then˜g(z)is said to be the best dominant of(3.1).We remark that the best dominant is unique up to a rotation of U.

Theorem 3.1Letµ≥-1,η∈{-1,0,1},0≤ρ＜1,0≤δ＜1,ρ+δ/=1 and-1≤B＜A≤1.Iff(z)∈Apsatisfesf(z)/=0 in 0＜|z|＜1,f′(z)/=0 whenη/=1,and

where

then

ProofLet us defne the functionP(z)in U by

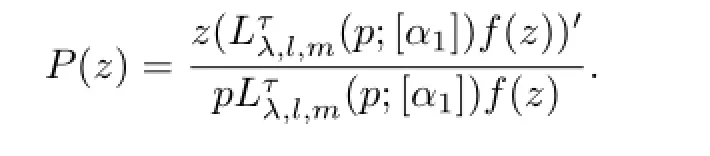
ThenP(z)is analytic in U and

From(3.2)and(3.4),we have

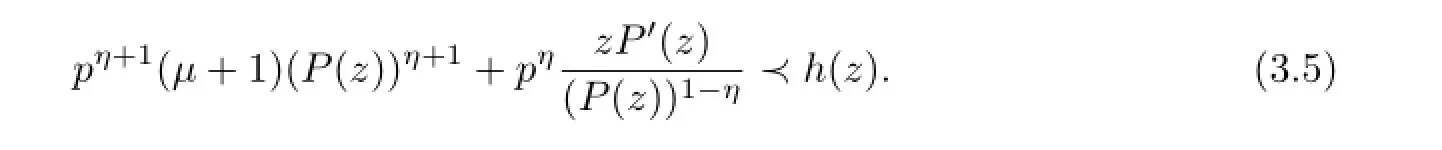
Let

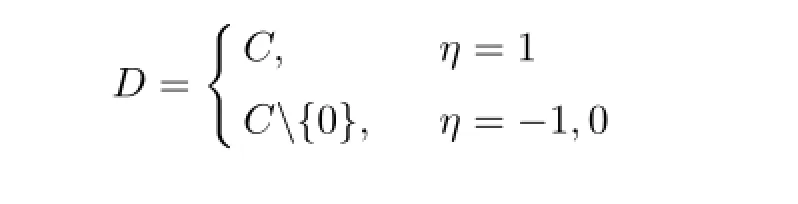
and choose

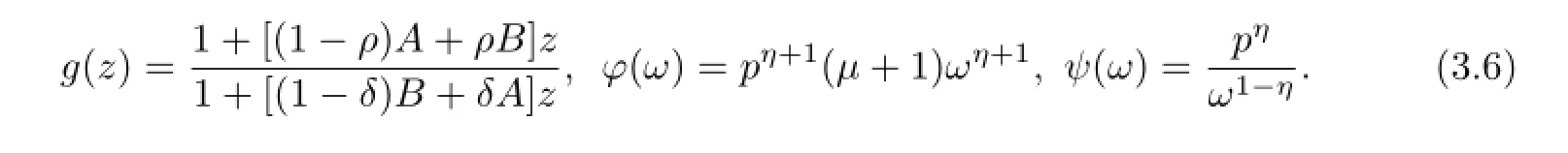
Theng(z)is analytic and univalent in U,g(0)=P(0)=1,P(U)⊂D,φ(ω)andψ(ω)satisfy the conditions of Lemma 3.1.The function

is univalent and starlike in U because

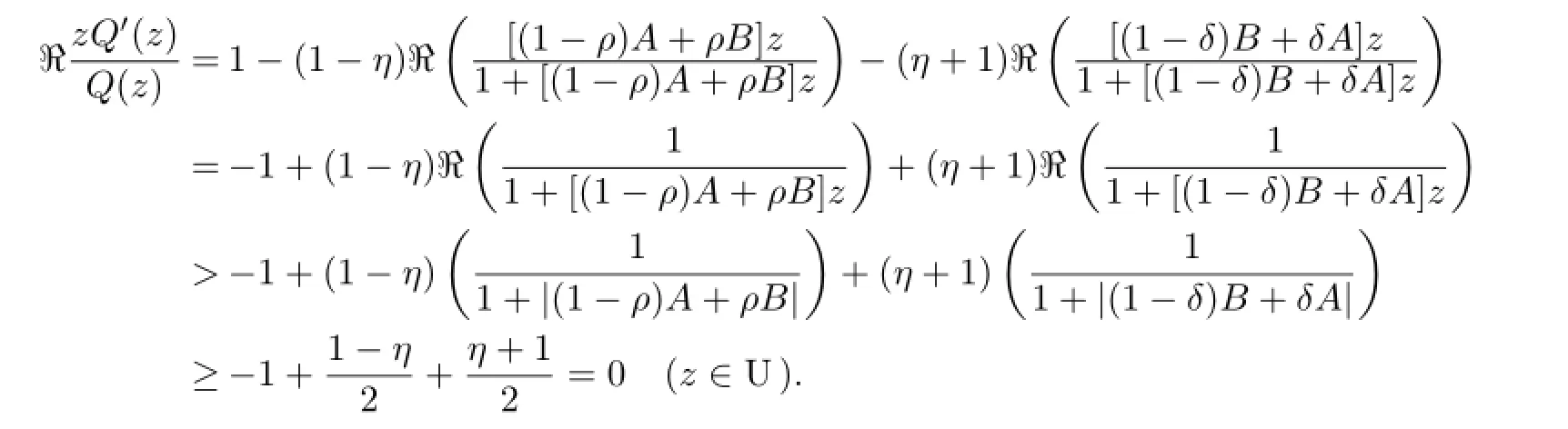
Further,we have

and

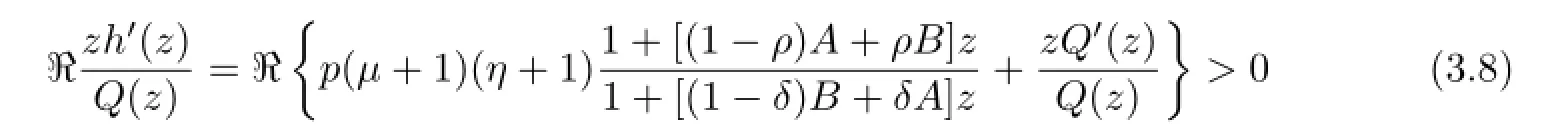
forz∈U.The inequality(3.8)shows that the functionh(z)is close-to-convex and univalent in U.Now it follows from(3.4)～(3.8)that

Corollary 3.1Letµ≥-1,η∈{-1,0,1},0≤ρ＜1,0≤δ＜1,ρ+δ/=1 and-1≤B＜A≤1.Iff(z)∈Apsatisfesf(z)/=0 in 0＜|z|＜1,f′(z)/=0 whenη/=1,and

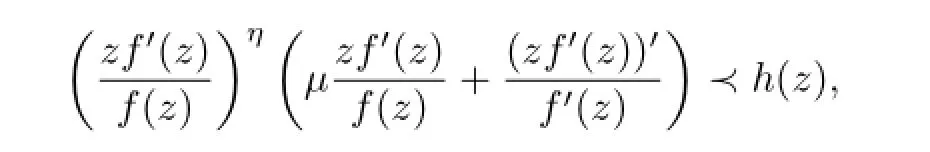
where

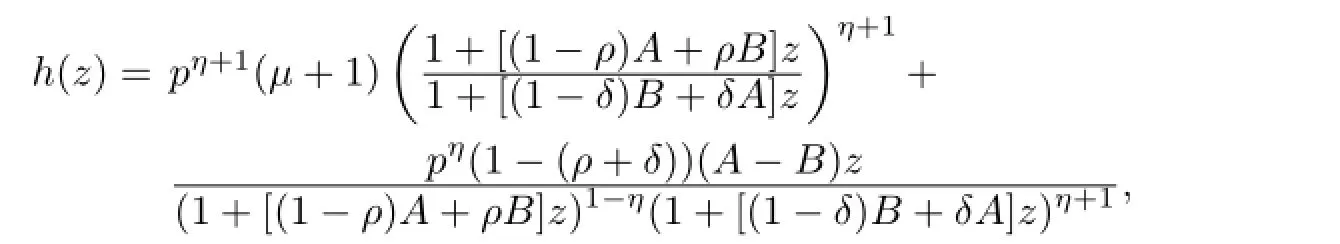
thenf(z)∈Sp[ρ,δ,A,B].

In the same way,we can also prove the following theorem.

Theorem 3.2Letµ≥-1,η∈{-1,0,1},0≤ρ＜1,0≤δ＜1,ρ+δ/=1 and-1≤B＜A≤1.Iff(z)∈Apsatisfesf(z)/=0 in 0＜|z|＜1,f′(z)/=0 whenη/=1 and

where

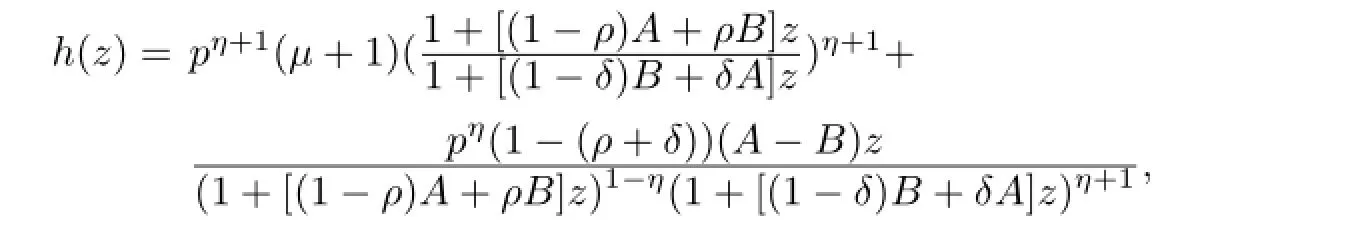
thenf(z)∈LKτ,p[α1;ρ,δ,A,B].

Corollary 3.2Letµ≥-1,η∈{-1,0,1},0≤ρ＜1,0≤δ＜1,ρ+δ/=1 and-1≤B＜A≤1.Iff(z)∈Apsatisfesf(z)/=0 in 0＜|z|＜1,f′(z)/=0 whenη/=1,and

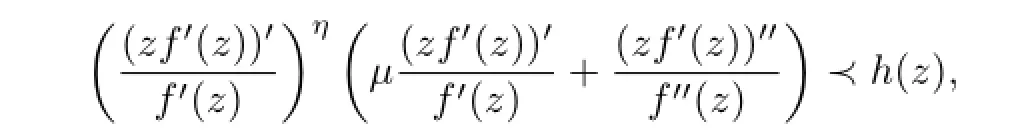
wherethenf(z)∈Kp[ρ,δ,A,B].

Next,using the method in[16],we can obtain the radius problems of the classesSp[A,B,ρ,δ] andKp[A,B,ρ,δ].

Theorem 3.3Letβ≥0,iff(z)∈Sp[A,B,ρ,δ],then

where

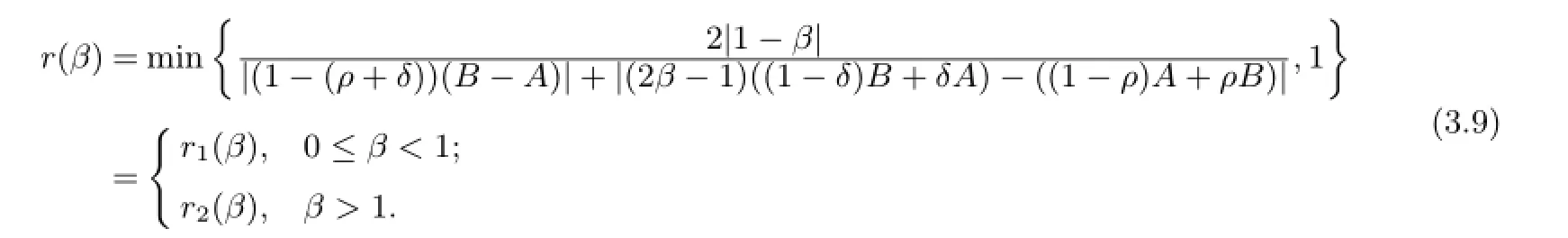
Making use of Theorem 3.3,we can obtain the following consequence.

Corollary 3.3Letβ≥0,iff(z)∈Kp[A,B,ρ,δ].Then

wherer1(β)andr2(β)given by(3.9).

We remark in conclusion that,by suitably specializing the parameters involved in the results presented in this paper,we can deduce numerous further corollaries and consequences of each of these results.

[References]

[1]ARIF M,NOOR K I,RAZA M,et al.Some properties of a generalized class of analytic functions related with Janowski functions[J].Abstract and Applied Analysis,Volume 2012,Article ID 279843,11 pages, doi:10.1155/2012/279843.

[2]JANOWSKI W.Some extremal problems for certain families of analytic functions[J].Ann Polon Math, 1973,28(3):297-326.

[3]POLATO˜GLU Y,BOLCAL M,S¸EN A,et al.A study on the generalization of Janowski functions in the unit disc[J].Acta Mathematica Academiae Paedagogicae Ny´ıregyh´aziensis,2006,22(1):27-31.

[4]DZIOK J,SRIVASTAVA H M.Classes of analytic functions associated with the generalized hypergeometric function[J].Applied Mathematics and Computation,1999,103(1):1-13.

[5]DZIOK J,SRIVASTAVA H M.Certain subclasses of analytic functions associated with the generalized hypergeometric function[J].Integral Transforms and Special Functions,2003,14(1):7-18.

[6]SRIVASTAVA H M,LI Shu-hai,TANG Huo.Certain classes ofk-uniformly close-to-convex functions and other related functions defned by using the Dziok-Srivastava operator[J].Bulletin of Mathematical Analysis and Applications,2009,1(3):49-63.

[7]EKER S S,S¸EKER B.On a class of multivalent functions defned by Sˇalˇagean operator[J].General Mathematics,2007,15:154-163.

[8]CARLSON B C,SHAFFER D B.Starlike and prestarlike hypergeometric functions[J].SIAM J Math Anal, 1984,15(4):737-745.

[9]OWA S.On the distortion theorems I[J].Kyungpook Math J,1978,18(1):53-59.

[10]RUSSCHEWEYH S.New criteria for univalent functions[J].Proc Amer Math Soc,1975,49(1):109-115.

[11]SˇALˇAGEAN G S.Subclasses of Univalent Functions:Lecture Notes in Mathematics[C].Berlin Heidelberg and NewYork:Springer-Verlag,1983,1013:362-372.

[12]SARKAR N,GOSWAMI P,DZIOK J,et al.Subordinations for multivalent analytic functions associated with wright generalized hypergeometric function[J].Tamkang Journal of Mathematics,2013,44(1):61-71.

[13]AOUF M K,SEOUDY T M.Classes of analytic functions related to the Dziok-Srivastava operator[J]. Integral Transforms and Special Functions,2011,22(6):423-430.

[14]MILLER S S,MOCANU P T.On some classes of frst-order diferential subordinations[J].Michigan Math J,1985,32(2):185-195.

[15]MILLER S S,MOCANU P T.Diferential Subordinations:Theory and Applications[M].New York:Maroel Pekker,2000.

[16]ALI R M,MOHD M H,LEE S K,et al.Radii of starlikeness,parabolic starlikeness and strong starlikeness for Janowski starlike functions with complex parameters[J].Tamsui Oxford Journal of Information and Mathematical Sciences,2011,27(3):253-267.

[17]MISHRA A K,SOREN M M.A generalization of the Srivastava-Attiya transform and associated classes[J]. Integral Transforms and Special Functions,2012,23(11):831-846.

[18]DUREN P L.Univalent functions.Grundlehren der Mathematischen Wissenschaften,Band 259[M].New York:Springer-Verlag,1983.

O174.51

:A

1002–0462(2016)04–0379–11

2000 MR Subject Classifcation:30C45,30C50,26D15