Kac Determinant Formula for the q-deformed Virasoro Algebra of Hom-type

WANG Meng-pingWU Lin-li

(1.School of Mathematics and Statistics,Henan University,Kaifeng475004,China;2.Institute of Contemporary Mathematics,Henan University,Kaifeng475004,China)

Kac Determinant Formula for the q-deformed Virasoro Algebra of Hom-type

QI Huan-ge1,CHENG Yong-sheng1,2,WANG Meng-ping1,WU Lin-li1

(1.School of Mathematics and Statistics,Henan University,Kaifeng475004,China;2.Institute of Contemporary Mathematics,Henan University,Kaifeng475004,China)

We investigate the highest weight representations of theq-deformed Virasoro algebra of Hom-type.In order to determine its unitarity and irreducible highest weight representations,we present its Kac determinant formula whenqis nonzero and non-root of unity.

theq-deformed Virasoro algebra of Hom-type;unitary highest weight representation;Kac determinant formula

§1.Introduction

The Virasoro algebra is an infnite dimensional Lie algebra and plays important roles in mathematics and physics[910].Its unitary representations and irreducible fnite dimensional representation are studied in[1,5,8].We expect some new aspects of physical applications of quantum groups through aq-deformation of the Virasoro algebra.Hom-Lie algebras were introduced by Hartig,Larson and Silvestrov in[6]as part of a study of deformations of the Witt and the Virasoro algebras(also see[2]).A Hom-Lie algebra is a triple(L,[·,·],α)consisting of a vector space L,a linear map[·,·]:L⊗L→Land a vector space homomorphismα:L→Lsatisfying the skewsymmetry andfor allx,y,z∈Lcalled Hom-Jacobi identity.The structure and representation theory of theq-deformed Virasoro algebra and its relative algebras were studied in[3,4,7,11].In particular, in[7],the author introduced aq-deformed Virasoro algebra of Hom-type and gave its Harish-Chandra modules.A basic tool in the representation theory of infnite dimensional Lie algebras is the determinant formula.This is the determinant of the matrix of inner products of a basis for the Verma modules.The determinant formula is crucial to investigate the unitarity and non-unitarity of the representations

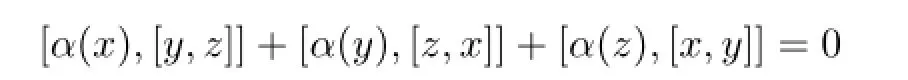
In this paper,we defne the Shapovalov form and study Kac determinant formula in order to obtain some unitary irreducible highest weight representations of theq-deformed Virasoro algebra of Hom-type.The properties of Kac determinant formula and some consequences for unitary irreducible highest weight weight representations are obtained.However,we may mention that in our case,becauseqis non-zero and non-root of unity,theq-deformed Virasoro algebra of Hom-type is not a Lie algebra,the structural constants are not linearly dependent on their gradings,in this case,the algebra is called non-linear,and this renders the computation of Kac determinant of theq-deformed Virasoro algebra of Hom-type nontrivial.

§2.The q-deformed Virasoro Algebra of Hom-type and Its Verma Representation

We develop some techniques in[3,4,7]to construct aq-deformed Virasoro algebra.LetAqbe the nonassociative algebra with basiswith the following product

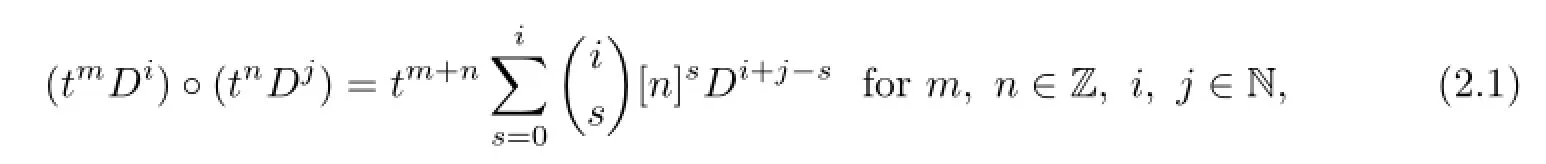
whereDis aq-derivation fromtodefned byand[m]form∈Z denotes theq-numberas a fxed non-root of unity.One can easily check that in general,

DenoteLn=-tnDand set Lq=span{Ln,|n∈Z}.We defne theq-bracket

We call Lqunder theq-bracket[·,·]theq-deformed Witt algebra.Similar with[3,7],we can easily obtain that.

Theorem 2.1(1)Set

Then(Lq,[·,·],αq)is a Hom-Lie algebra.

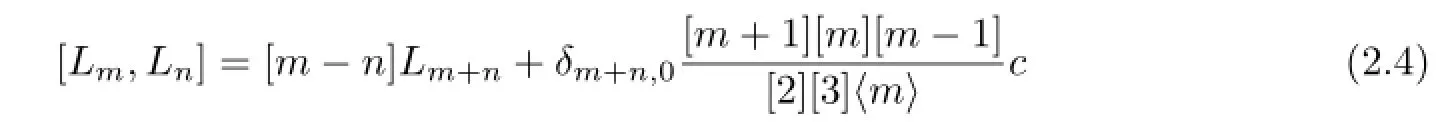
for allm,n∈Z.

In general,since(Lq,◦)is not an associative algebra,we see the algebrais not a Lie algebra ifqis a nonzero and non-root of unity.In[7],the universal enveloping algebra ofis given by

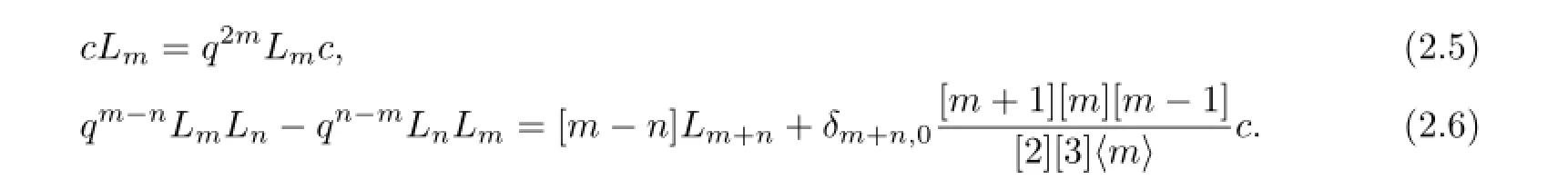
Similarly,U(bLq)has the triangular decomposition as follow

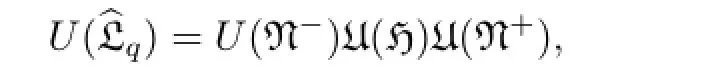
where N-and N+are generated byLnforn＜0 andn＞0 respectively,H is generated byL0andc.

Defnition 2.2A vector spaceVover C is called an-module,if there is a bilinear mapsuch that

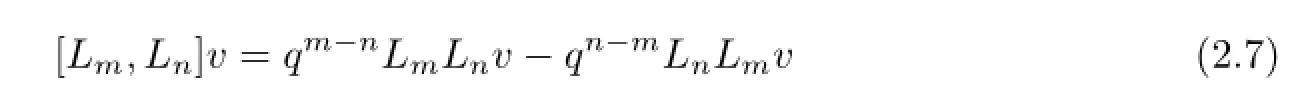
for allm,n∈Z,v∈V.

Defnition 2.3A representation ofof Hom-type in a linear spaceVis called a highest weight representation if there is an elementv∈V,and two numbersC,h∈C,such that

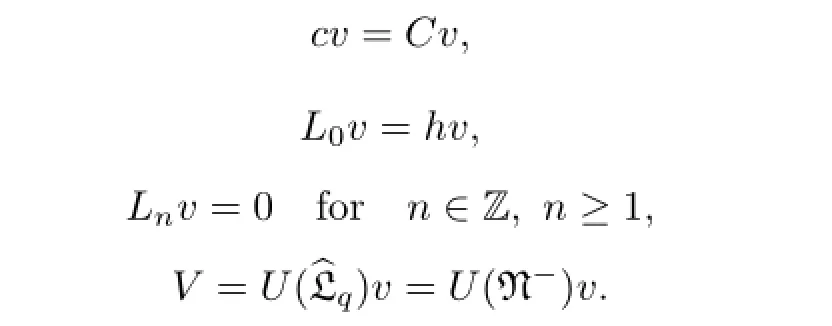
The vectorvis called a highest weight vector and(C,h)is the highest weight.

An anti-linear anti-involutionωon a complex algebraAis a mapA→Asuch that

and

Defnition 2.4Letω:be an anti-linear anti-involution ofLetπ:gl(V)be a representation ofin a linear spaceVequipped with an Hermitian form〈·,·〉.The form〈·,·〉is called contravariant with respect toωiffor allThe representationπis said to be unitary if in addition〈v,v〉＞0 for all nonzerov∈V.

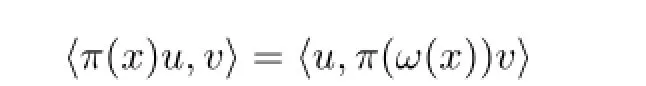
Proposition 2.5Defnethenωis an anti-linear antiinvolution of

Lemma 2.6LetVbe a representation ofand

whereVλ={v∈V|hv=λ(h)vfor allh∈H}and H∗is the dual vector space of H.Then every subrepresentationUofVrespects this decomposition in the sense that

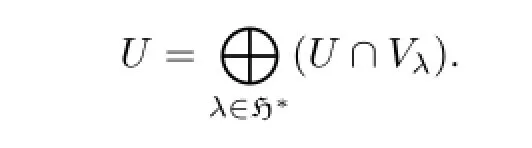
Proposition 2.7Any highest weight representationVofwith highest weigh(C,h) has the decomposition

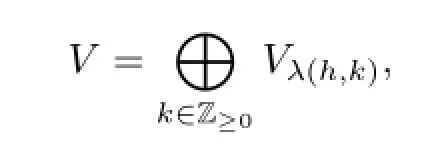
ProofBy(2.4)and(2.6),we have

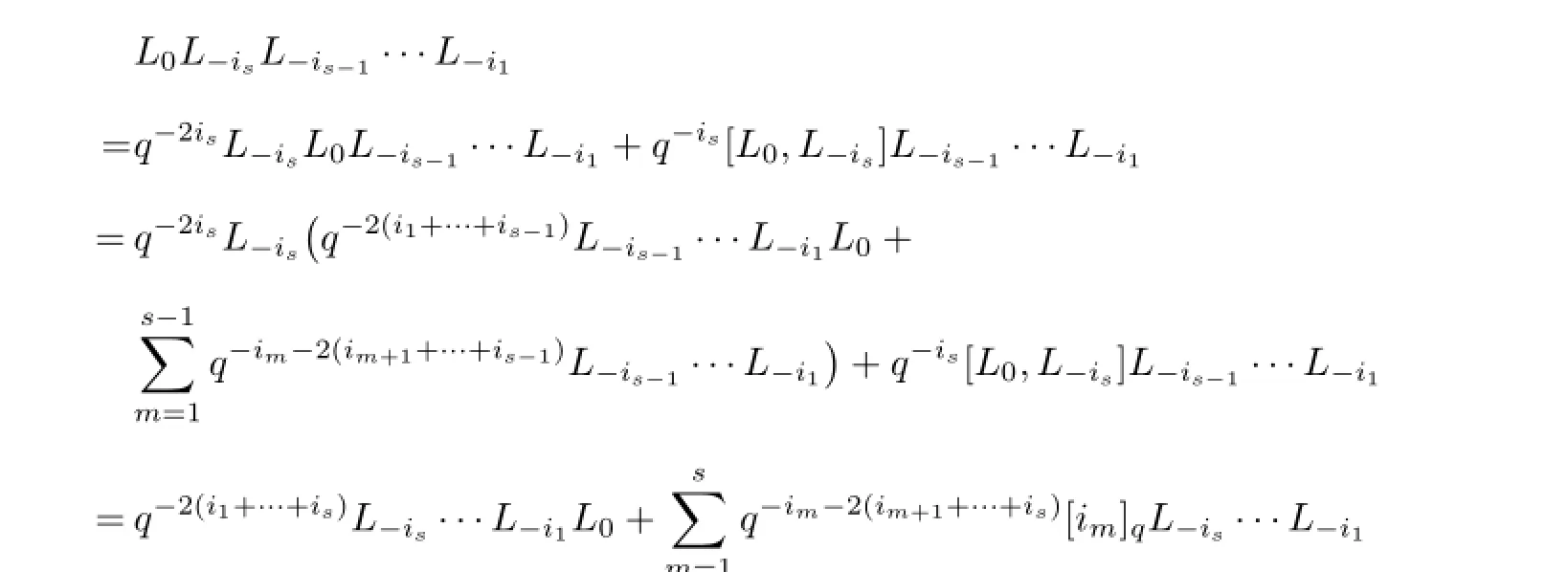
and

Hence

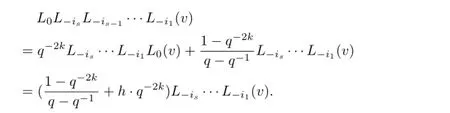
Theorem 2.8A unitary highest weight representationVofbLqis irreducible.

ProofIfUis a subrepresentation ofV,thenV=ULU⊥,using Lemma 2.6 and Proposition 2.7,we obtain

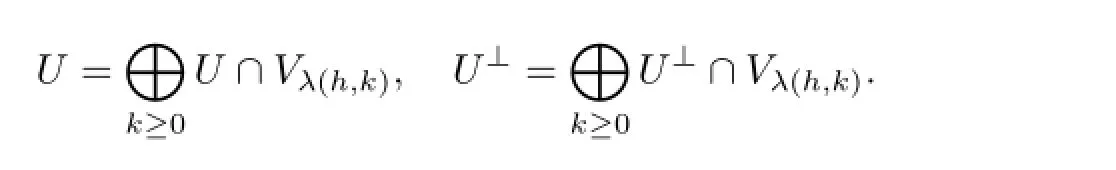
SinceVλ(h,0)is one-dimensional and spanned by some nonzero highest weight vectorv,we have eitherv∈Uorv∈U⊥.Thus eitherU=VorU=0.

Defnition 2.9A highest weight representationM(C,h)ofwith highest weight vectorvand highest weight(C,h)is called a Verma representation if,for any highest weight representationVofwith highest weight vectoruand highest weight(C,h),there exists a unique epimorphismφ:M(C,h)→Vof-modules which mapsvtou.

Similar with Lemma 2.7 and Proposition 3.3 in[9],we have

Proposition 2.10a)The Verma representationM(C,h)has the decomposition

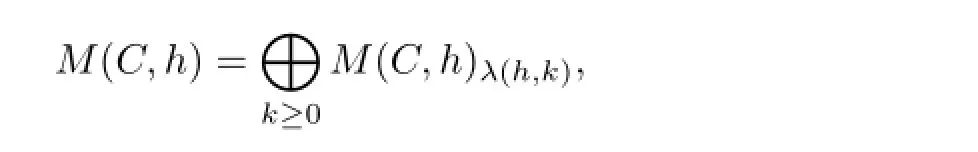
whereM(C,h)λ(h,k)is theλ(h,k)-eigenspace ofL0spanned by vectors of the form

b)M(C,h)is indecomposable,i.e.,we cannot fnd nontrivial subrepresentationsW1,W2ofM(C,h)such that

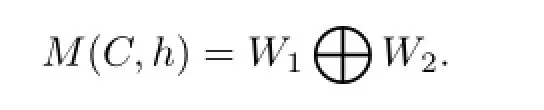
c)M(C,h)has a unique maximal proper subrepresentationJ(C,h)and

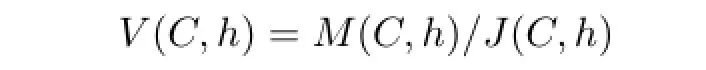
is the unique irreducible highest weight representation with highest weight(C,h).

Proposition 2.11LetC,h∈R.Then

a)There is a unique contravariant Hermitian form〈·|·〉onM(C,h)such that〈v|v〉=1;

c)J(C,h)=ker〈·|·〉≡{u∈M(C,h)|〈u|w〉=0 for allw∈M(C,h)}.

ProofWe just prove the part b).Ifx∈M(C,h)λ(h,k)andy∈M(C,h)λ(h,l)withk/=l, then we have

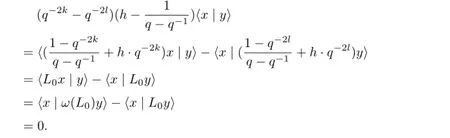
The form is called Shapovalov’s form.

§3.Kac Determinant Formula of the q-deformed Virasoro Algebra of Hom-type

In this section,we present the Kac determinant of theq-deformed Virasoro algebra of Homtype.It is easy to know that there exists at most one unitary highest weight representation offor a given highest weight(C,h),namelyV(C,h).

Proposition 3.1IfV(C,h)is unitary,thenh≥0.

ProofSince

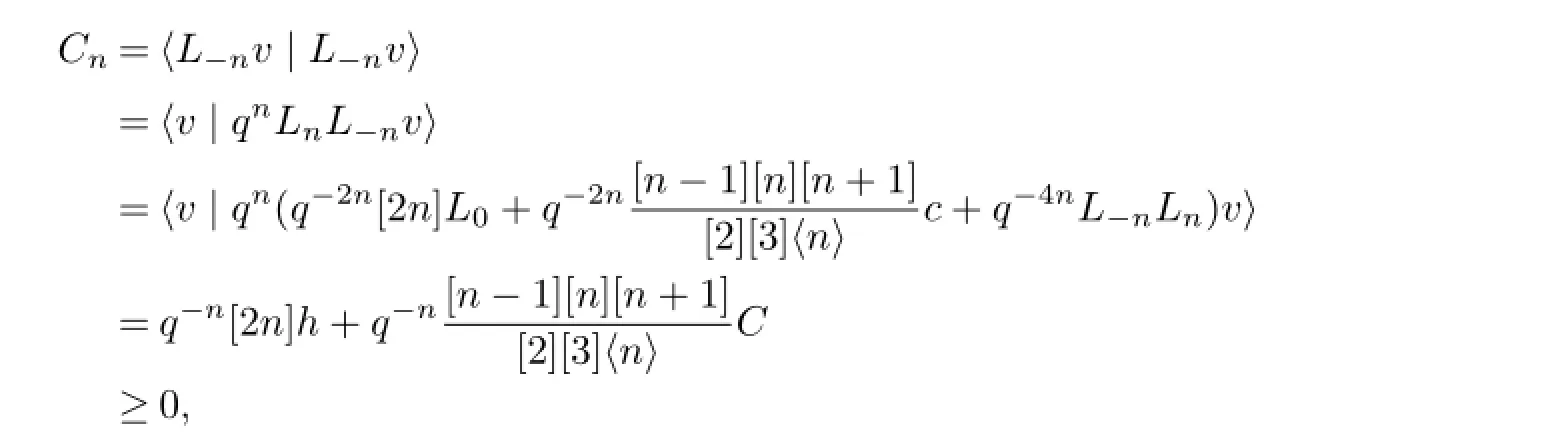
whereIn particular,thush≥0.

Let

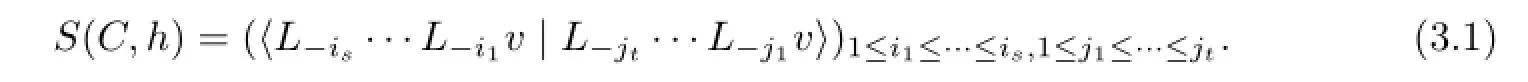
SinceM(C,h)is a direct sum of fnite-dimensional pairwise orthogonal subspacesM(C,h)λ(h,k),k≥0,the matrixS(C,h)is also a direct sum of matricesSk(C,h),k≥0,whereSk(C,h)is the matrix of the Shapovalov form restricted toM(C,h)λ(h,k),that is,

whereP(n)denotes the set of all partitions ofn.Defne

Lemma 3.2Letit,···,i1≥1 andjs,···,j1≥1,wheres,t≥1.Then we have

(1)

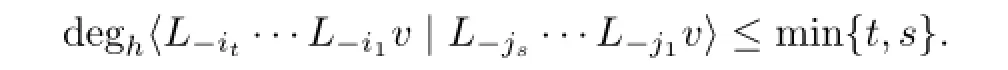
(2)

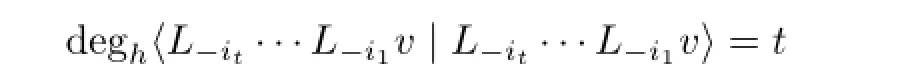
and the coefcient ofhtis positive.

(3)If(it,···,i1)/=(jt,···,j1),then

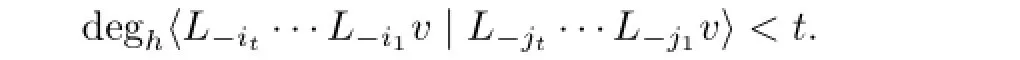
Letf,g∈C[h],we callf～gif degh(f-g)＜min{deghf,deghg}.It is easy to see that～is an equivalence relation on the set of complex polynomials inh.It is easy to obtain that

Proposition 3.3

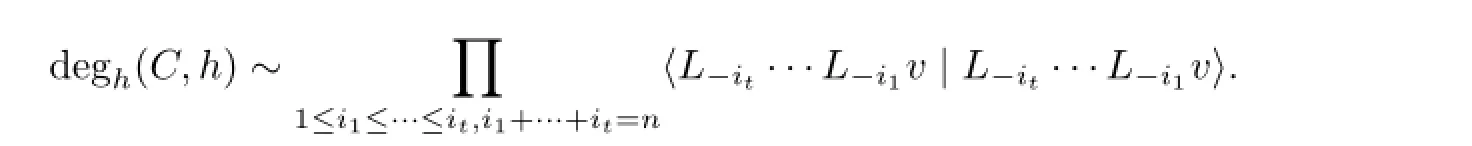
Lemma 3.4Letk∈Z+,then

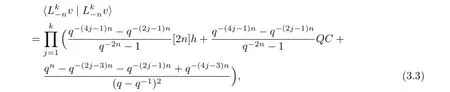
ProofWe use induction onk.Fork=1,we can easily obtain

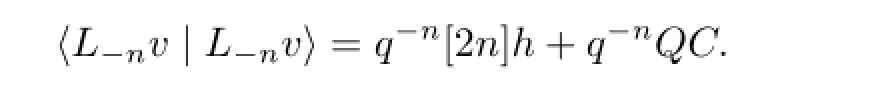
Suppose that(3.3)holds fork-1,using the fact that

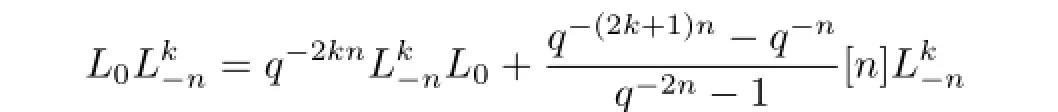
and

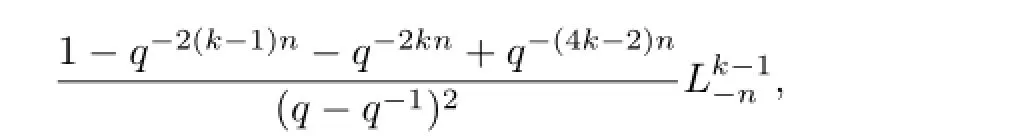
we have

Lemma 3.5Leti1,···,is,j1,···,js∈Z+,whereit/=jrfort/=r.Then

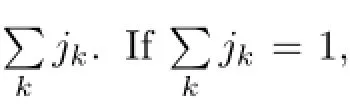
For the induction step,we have

Thus

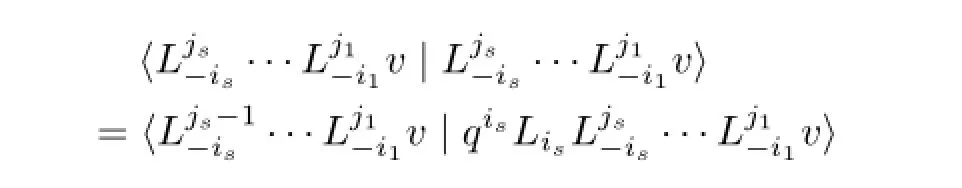
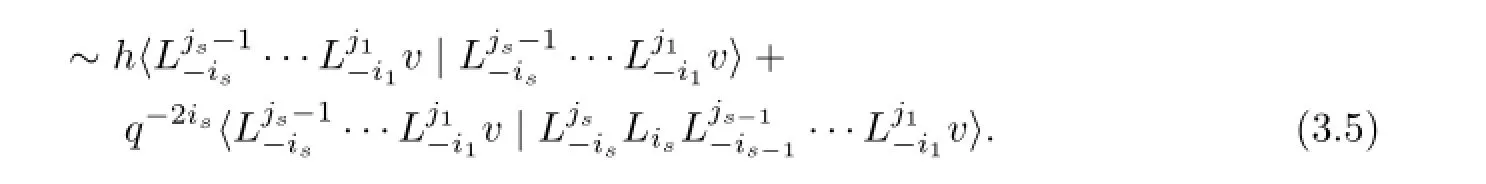
Using the induction hypothesis,we have

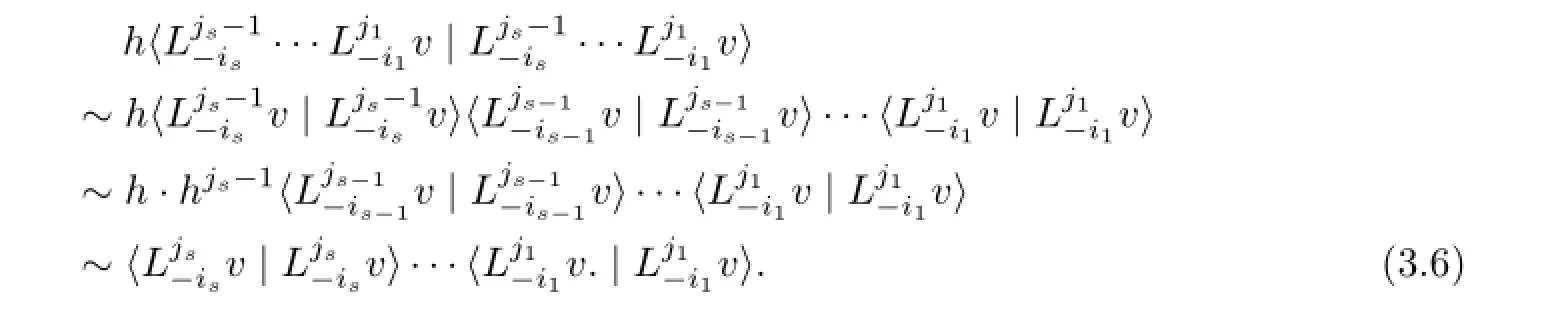
It is easy to obtain that

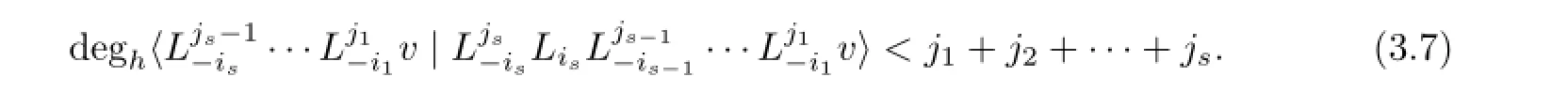
So the result comes from(12),(13)and(14).

Using Lemma 3.4 and 3.5,we obtain our main theorem.

Theorem 3.6

wherem(r,s)is the number of partitions ofnin whichrappears exactlystimes.

[1]CHARI V,PRESSLEY A.Unitary representations of the Virasoro algebra and a conjecture of Kac[J]. Compo Math,1988,67:315-342.

[2]CHENG Yong-sheng,LIU Guo-jing.Monoidal category approach to dual Hom-quasi-Hopf algebras[J].Chin Quart J of Math,2015,30(2):218-226.

[3]CHENG Yong-sheng,SU Yu-cai.(Co)Homology and universal central extension of Hom-Leibniz algebras[J]. Acta Math Sin(Engl Ser),2011,27(5):813-830.

[4]CHENG Yong-sheng,YANG Heng-yun.Low-dimensional cohomology of theq-deformed Heisenberg-Virasoro algebra of Hom-type[J].Front Math China,2010,5(4):607-622.

[5]GODDARD P,KENT A,OLIVE D.Unitary representations of the Virasoro and super-Virasoro algebras[J]. Commun Math Phys,1986,103:105-119.

[6]HARTWIG J T,LARSSON D,SILVESTROV S D.Deformations of Lie algebras usingσ-derivations[J].J Algebra,2006,295:314-361.

[7]LIU Ke-qin.A class of Harish-Chandra modules for theq-deformed Virasoro algebra[J].J Algebra,1995, 171:606-630.

[8]JAKOBSEN H P,KAC V G.A new class of unitarizable highest weight representations of infnite-dimensional Lie algebras[J].J Funct Analysis,1989,82(1):69-90.

[9]KAC V G,RAINA A K.Bombay lectures on highest weight representations of infnite-dimensional Lie algebras[M].Singapore:Word Scientifc,1987.

[10]SU Yu-cai,ZHAO Kai-ming.Generalized Virasoro algebras and super-Virasoro algebras and modules of the intermediate series[J].J Algebra,2002,252:1-19.

[11]ZHAO Kai-ming.Representation ofq-analogue of the Virasoro algebra[J].Northeast Math J,1997,13(2): 197-204.

O152.5

:A

1002–0462(2016)04–0331–09

Received date:2016-01-28

Foundation item:Supported by the National Natural Science Foundation of China(11047030);Supported by the Science and Technology Program of Henan Province(152300410061)

Biography:CHENG Yong-sheng(corresponding author)(1973-),male,native of Lankao,Henan,an associate professor of Henan University,Ph.D.,engages in Lie theory.

2000 MR Subject Classifcation:17B10,17B65,17B68