Complete Convergence for Weighted Sums of Negatively Superadditive Dependent Random Variables

(School of Mathematical Sciences,Anhui University,Hefei230601,China)

Complete Convergence for Weighted Sums of Negatively Superadditive Dependent Random Variables

WANG Qiang,ZHOU De-xia,DU Ling,XIAO Ru,WANG Xue-jun

(School of Mathematical Sciences,Anhui University,Hefei230601,China)

In the paper,the complete convergence for the maximum of weighted sums of negatively superadditive dependent(NSD,in short)random variables is investigated by using the Rosenthal type inequality.Some sufcient conditions are presented to prove the complete convergence.The result obtained in the paper generalizes some corresponding ones for independent random variables and negatively associated random variables.

negatively superadditive dependent random variables;Rosenthal-type inequality;complete convergence

§1.Introduction

Firstly,let us recall the defnitions of negatively associated random variables and negatively superadditive dependent random variables.The concept of negatively associated random variables was introduced by Alam and Saxena[1]and carefully studied by Joag-Dev and Proschan[2]as follows.

Defnition 1.1A fnite collection of random variablesX1,X2,···,Xnis said to be negatively associated(NA)if for every pair of disjoint subsetsA1,A2of{1,2,···,n},wheneverfandgare coordinatewise nondecreasing such that this covariance exists.An infnite sequence{Xn,n≥1}is NA if every fnite subcollection is NA.

The next dependence notion is negatively superadditive dependence,which is weaker than negative association.The concept of negatively superadditive dependent random variables was introduced by Hu[3]as follows.

Defnition 1.2[4]A functionφ:Rn→R is called superadditive ifφ(x∨y)+φ(x∧y)≥φ(x)+φ(y)for allx,y∈Rn,where∨stands for componentwise maximum and∧denotes componentwise minimum.

Defnition 1.3[3]A random vectorX=(X1,X2,···,Xn)is said to be negatively superadditive dependent(NSD)if

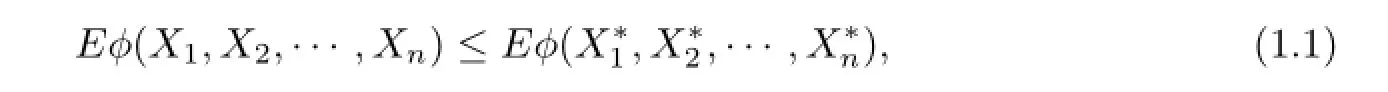
whereare independent such thatandXihave the same distribution for eachiandφis a superadditive function such that the expectations in(1.1)exist.

A sequence{Xn,n≥1}of random variables is said to be NSD if for alln≥1(X1,X2,···, Xn)is NSD.

The concept of NSD random variables was introduced by Hu[3],which was based on the class of superadditive functions.Hu[3]gave an example illustrating that NSD does not imply NA,and Hu posed an open problem whether NA implies NSD.In addition,Hu[3]provided some basic properties and three structural theorems of NSD.Christofdes and Vaggelatou[5]solved this open problem and indicated that NA implies NSD.Negatively superadditive dependent structure is an extension of negatively associated structure and sometimes more useful than it and can be used to get many important probability inequalities.Eghbal et al[6]derived two maximal inequalities and strong law of large numbers of quadratic forms of NSD random variables under the assumption that{Xi,i≥1}is a sequence of nonnegative NSD random variables withfor alli≥1 and somer＞1.Eghbal et al[7]provided some Kolmogorov inequality for quadratic formsand weighted quadratic formswhere{Xi,i≥1}is a sequence of nonnegative NSD uniformly bounded random variables. Shen et al[8]obtained Kolmogorov-type inequality and the almost sure convergence for NSD sequences.Wang et al[9]obtained the complete convergence for arrays of rowwise NSD random variables and gave its applications to nonparametric regression models.Shen et al[10]gave some applications of the Rosenthal-type inequality for NSD random variables.For more details about the probability limit behavior,one can refer to Wang et al[11],Pan et al[12],Wu and Wu[13],and so forth.Since NSD random variables are much weaker than independent random variables and NA random variables,studying the limit behavior of NSD sequence is of interest.The main purpose of the paper is to study the complete convergence for weighted sums of NSD random variables.

The following concept of stochastic domination will be used in the paper.

Defnition 1.4A sequence{Xn,n≥1}of random variables is said to be stochastically dominated by a random variableXif there exists a positive constantCsuch thatfor allx≥0 andn≥1.

Throughout the paper,letX1,X2,···be a sequence of NSD random variables defned on a fxed probability space(Ω,F,P).DenoteX+=max{0,X}andX-=max{0,-X}.LetCbe a positive constant which may be diferent in various places.「x⌉denotes the integer part ofx.

§2.Preliminary Lemmas

To prove the main results of the paper,we need the following important lemmas.The frst lemma comes from Hu[3].

Lemma 2.1Let{Xn,n≥1}be a sequence of NSD random variables and let{fn,n≥1}be a sequence of nondecreasing functions,then{fn(Xn),n≥1}is still a sequence of NSD random variables.

The next one is the Rosenthal type maximal inequality for NSD random variables,which was established by Wang et al[9].

Lemma 2.2Let{Xn,n≥1}be a sequence of NSD random variables withEXn=0 andE|Xn|p＜∞for somep≥2.Then there exists a positive constantCpdepending only onpsuch that

The last one is a basic property for stochastic domination.For the proof,one can refer to Wu[14],or Shen[15].

Lemma 2.3Let{Xn,n≥1}be a sequence of random variables which is stochastically dominated by a random variableX.Then for anyα＞0 andb＞0,

and

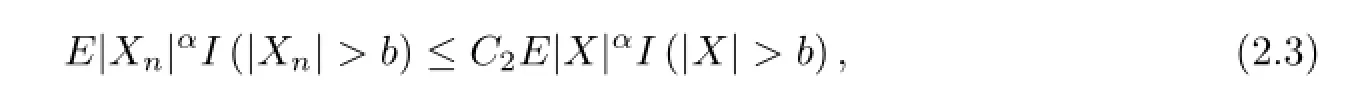
whereC1andC2are positive constants.Consequently,

§3.Main Results and Their Proofs

Theorem 3.1Let{Xn,n≥1}be a sequence of mean zero NSD random variables,which is stochastically dominated by a random variableXwithE|X|p＜∞for somep＞1/αand 1/2＜α≤1.Let{ani,1≤i≤n,n≥1}be an array of real numbers satisfying|ani|＞1 orani=0.If

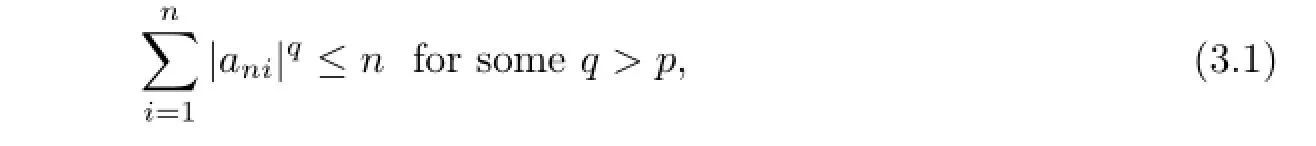
then for anyε＞0,

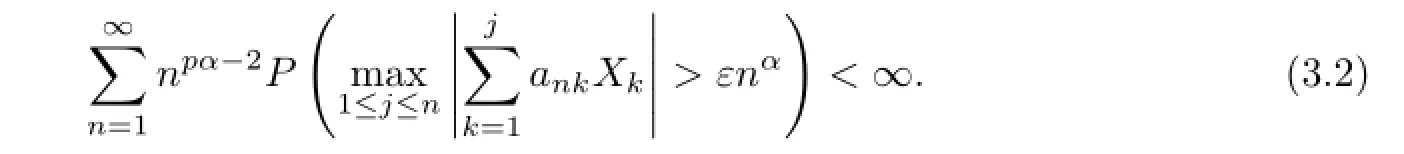
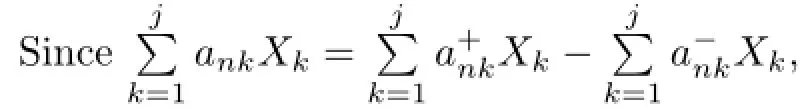
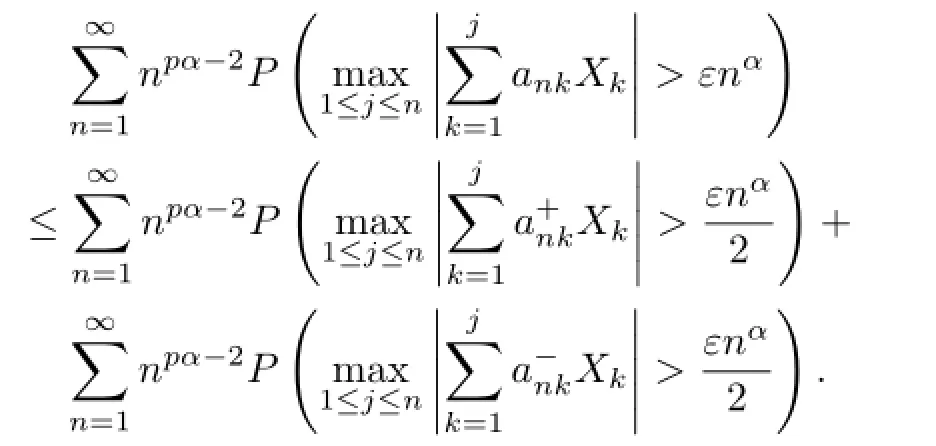
So without loss of generality,we may assume thatank≥0 for 1≤k≤nandn≥1.

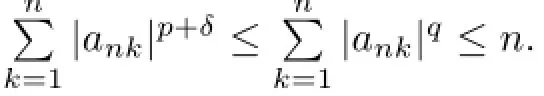
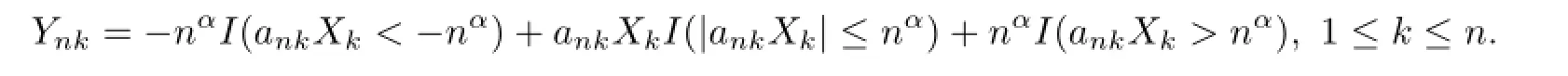
Thus,{Ynk-EYnk,1≤k≤n}are still NSD random variables from Lemma 1.1.SinceEXk=0,E|X|p＜∞andpα＞1,we have by Lemma 2.3,H¨older’s inequality and(3.1)that

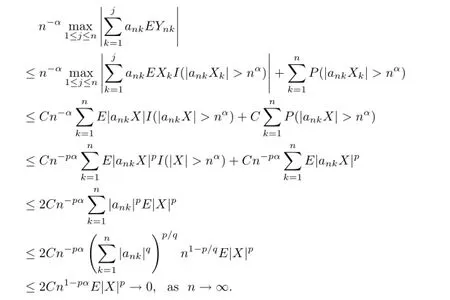
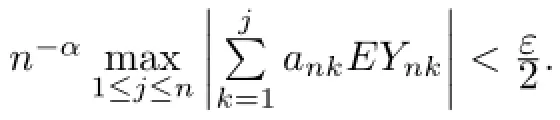
For 1≤j≤n-1 andn≥2,denote

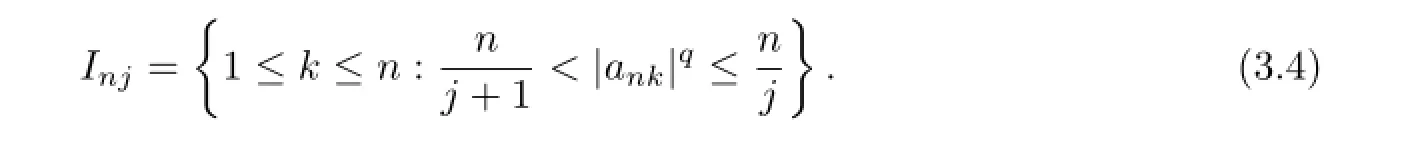
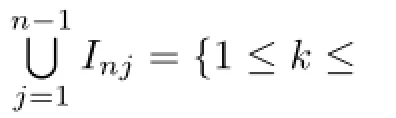
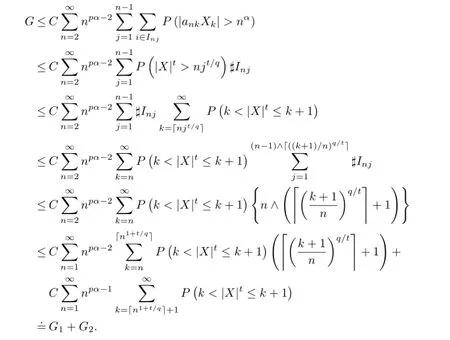
Sincepα-2-q/t=-α(q-p)-1＜-1,we have

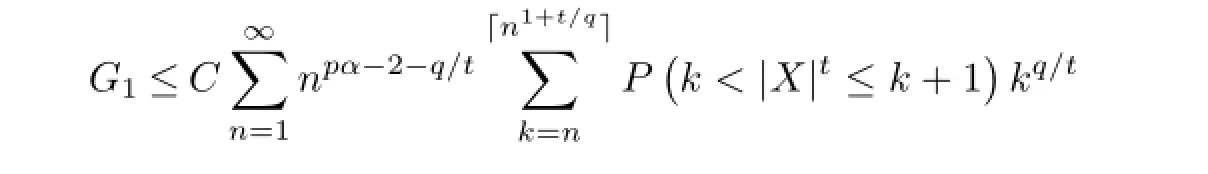
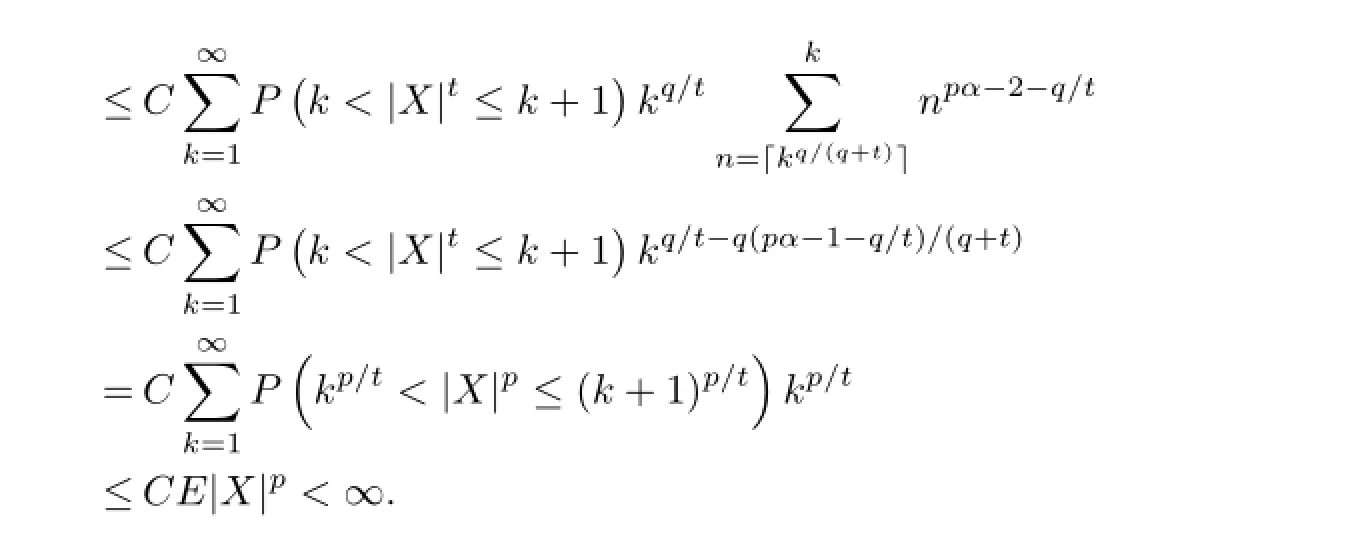
Similarly,

From the above statements,we can get thatG≤G1+G2＜∞.It remains to show thatH＜∞.

For anyr≥2,we have by Markov’s inequality,Lemma 2.2 andCr’s inequality that

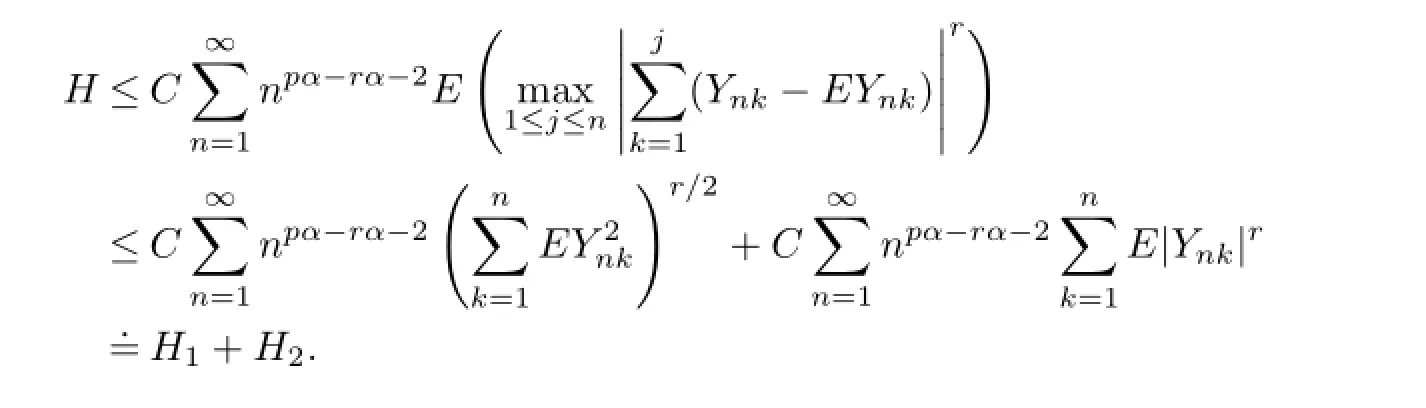
It is easy to check that forr≥qandn＞m≥1,

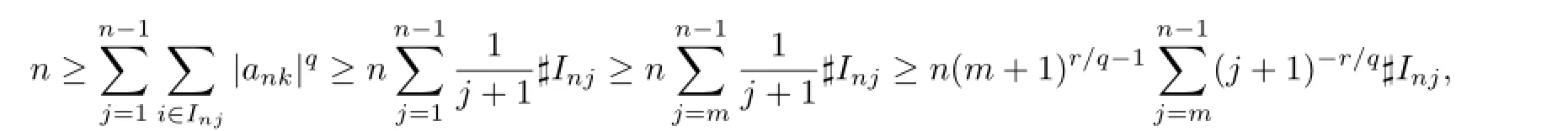
which implies that

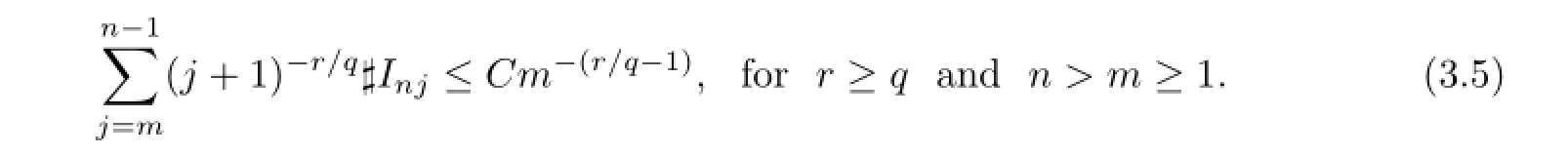
ForH1andH2,we will proceed with two cases.

(i)Ifp≥2,then we can takerlarge enough such thatr＞max{(pα-1)/(α-1/2),q}. Thus,pα-rα-2+r/2＜-1.ByCr’s inequality,we have

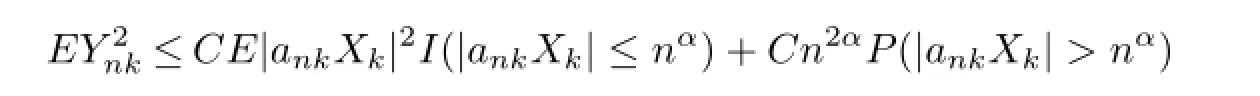
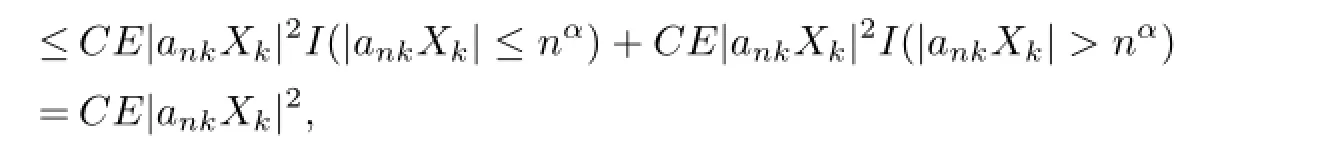
which implies that

We have byCr’s inequality again that

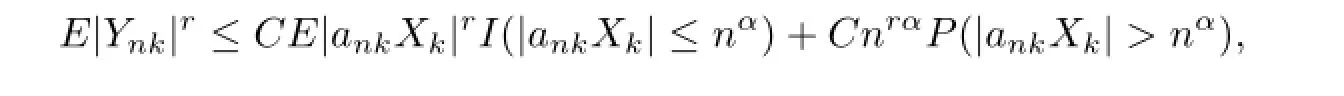
which implies that

We have proved that

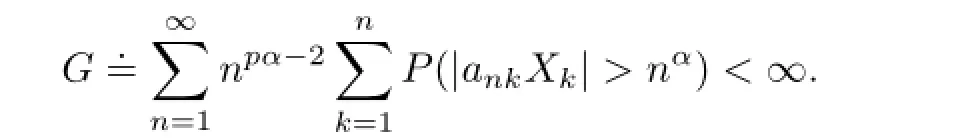
So in order to proveH＜∞,we need only to prove

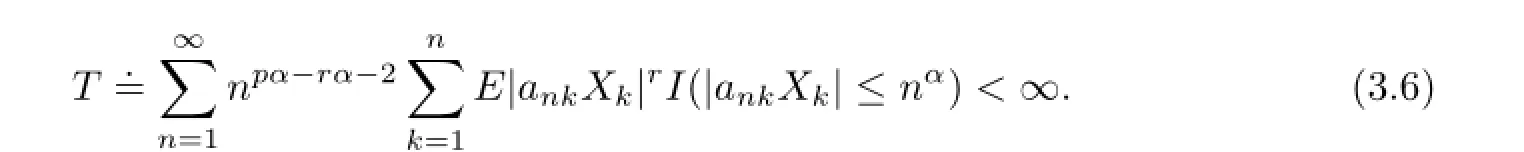
It follows by Lemma 2.3 again that

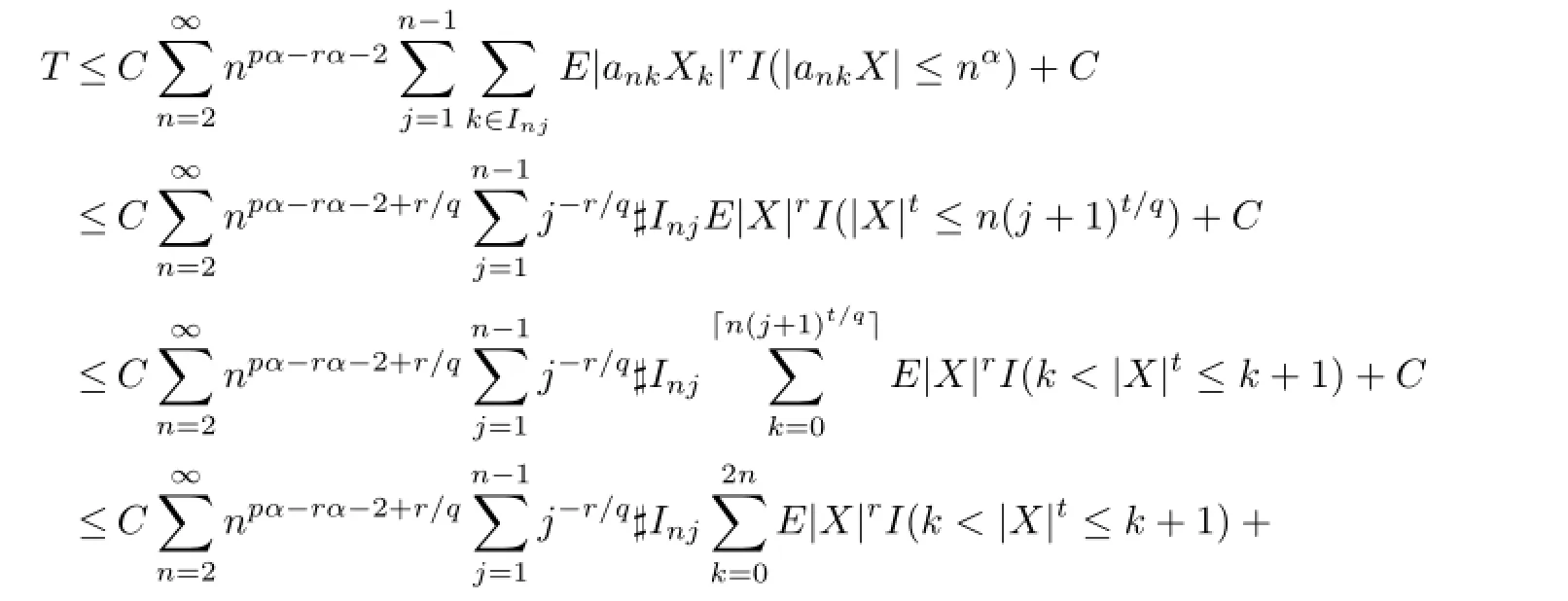
The factq＞pimplies thatpα-rα-2+r/q＜qα-rα-2+r/q=-(r-q)(α-1/q)-1＜-1. Therefore,

Sinceα=1/t+1/qandpα-2-q/t=pα-2-αq+1=-α(q-p)-1＜-1,we have that

FromT1＜∞andT2＜∞,we can get thatT＜∞,which implies(3.6).

(ii)Ifp＜2,then we taker=2.As mentioned above,we may assume thatp＜q＜2.Sincer＞q,as in the casep≥2,we haveH1=H2≤CE|X|p＜∞andH＜∞.This completes the proof of the theorem.

Ifaniin Theorem 3.1 is replaced byai,then we can get the following result.The proof is standard,so we omit the details.

Corollary 3.1Let{Xn,n≥1}be a sequence of mean zero NSD random variables,which is stochastically dominated by a random variableXwithE|X|p＜∞for somep＞1/αand 1/2＜α≤1.Let{ai,i≥1}be a sequence of real numbers satisfying|ai|＞1 orai=0.If

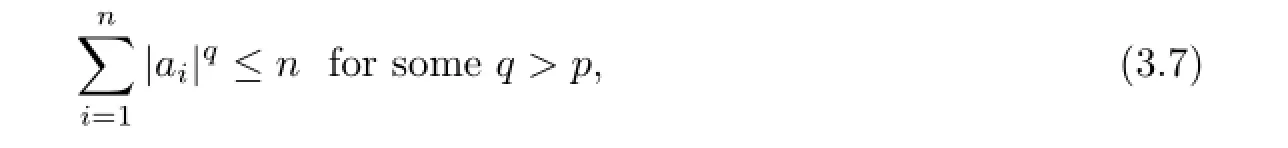
then for anyε＞0,

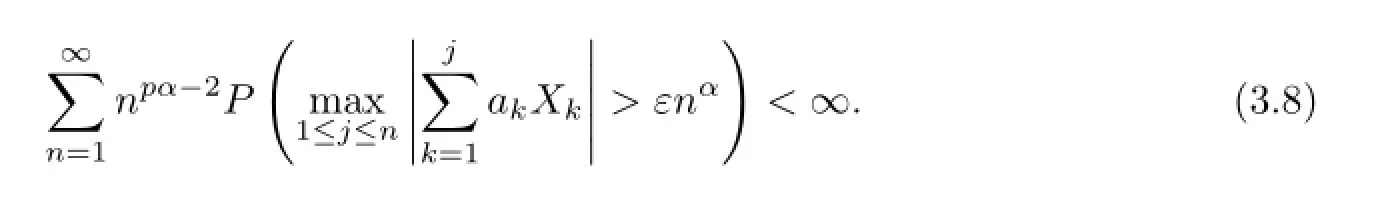
Consequently,

Remark 3.1Theorem 3.1 and Corollary 3.1 hold for NA random variables,since NSD includes NA as a special case.We should point out that the results of Theorem 3.1 and Corollary 3.1 for NA random variables are not obtained before.

Remark 3.2There are many arrays{ani,1≤i≤n,n≥1}of real numbers satisfying the conditions of Theorem 3.1.See for example,leta11=0 and forn≥2,

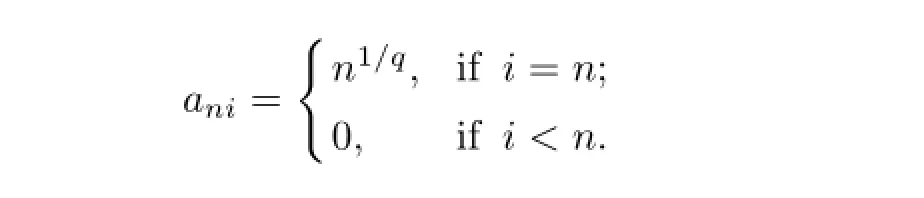
Then the array{ani,1≤i≤n,n≥1}satisfes the conditions of Theorem 3.1.

Another example of{ani,1≤i≤n,n≥1}can be seen as follows

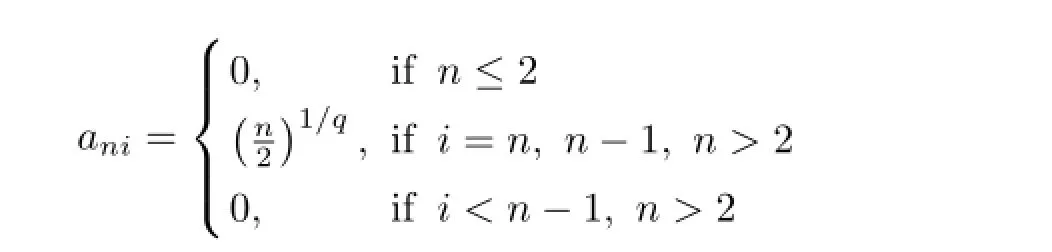
and so on.

AcknowledgementsThe authors are most grateful to the Editor and anonymous referees for careful reading of the manuscript and valuable suggestions which signifcantly improve earlier version of this paper.

[References]

[1]ALAM K,SAXENA K M L.Positive dependence in multivariate distributions[J].Communications in Statistics-Theory and Methods,1981,10:1183-1196.

[2]JOAG-DEV K,PROSCHAN F.Negative association of random variables with applications[J].Annals of Statistics,1983,11(1):286-295.

[3]HU Tai-zhong.Negatively superadditive dependence of random variables with applications[J].Chinese Journal of Applied Probability and Statistics,2000,16:133-144.

[4]KEMPERMAN J H B.On the FKG-inequalities for measures on a partially ordered space[J].Nederl Akad Wetensch Proc,1977,80A:313-331.

[5]CHRISTOFIDES T C,VAGGELATOU E.A connection between supermodular ordering and positive/negative association[J].Journal of Multivariate Analysis,2004,88:138-151.

[6]EGHBAL N,AMINI M,BOZORGNIA A.Some maximal inequalities for quadratic forms of negative superadditive dependence random variables[J].Statistics&Probability Letters,2000,80:587-591.

[7]EGHBAL N,AMINI M,BOZORGNIA A.On the Kolmogorov inequalities for quadratic forms of dependent uniformly bounded random variables[J].Statistics&Probability Letters,2011,81:1112-1120.

[8]SHEN Yan,WANG Xue-jun,YANG Wen-zhi,et al.Almost sure convergence theorem and strong stability for weighted sums of NSD random variables[J].Acta Mathematica Sinica,English Series,2013,29(4):743-756.

[9]WANG Xue-jun,DENG Xin,ZHENG Lu-lu,et al.Complete convergence for arrays of rowwise negatively superadditive-dependent random variables and its applications[J].Statistics:A Journal of Theoretical and Applied Statistics,2014,48(4):834-850.

[10]SHEN Ai-ting,ZHANG Ying,VOLODIN A.Applications of the Rosenthal-type inequality for negatively superadditive dependent random variables[J].Metrika,2015,78(3):295-311.

[11]WANG Xue-jun,HU Shu-he,YANG Wen-zhi.Some convergence results for arbitrary sequences under moment condition[J].Chinese Quarterly Journal of Mathematics,2011,26(4):585-589.

[12]PAN Jing,ZHU Ye-chun,ZOU Wei-yuan,et al.Some convergence results for sequences ofψ-mixing random variables[J].Chinese Quarterly Journal of Mathematics,2013,28(1):111-117.

[13]WU Yan-chun,WU Qun-ying.Complete convergence properties of the sums forρ-mixing sequences of random Variables[J].Chinese Quarterly Journal of Mathematics,2011,26(2):159-163.

[14]WU Qun-ying.Probability Limit Theory for Mixing Sequences[M].Beijing:Science Press,2006.

[15]SHEN Ai-ting.On the strong convergence rate for weighted sums of arrays of rowwise negatively orthant dependent random variables[J].RACSAM,2013,107(2):257-271.

O211.4

:A

1002–0462(2016)04–0359–10

Received date:2014-06-30

Foundation item:Supported by the Natural Science Foundation of Anhui Province(1508085J06);Supported by the Research Teaching Model Curriculum of Anhui University(xjyjkc1407);Supported by the Students Innovative Training Project of Anhui University(201510357118)

Biographies:WANG Qiang(1993-),female,native of Nantong,Jiangsu,B.S.D.,engages in statistics;WANG Xue-jun(1981-),male,native of Hefei,Anhui,an associate professor of Anhui Universiry,Ph.D.,engages in probability theory and mathematical statistics.

2000 MR Subject Classifcation:60F15