Common Fixed Points for Mappings with Quasi-Lipschitz Conditions on TVS-valued Cone Metric Spaces

(College of Science,Yanbian University,Yanji133002,China)

Common Fixed Points for Mappings with Quasi-Lipschitz Conditions on TVS-valued Cone Metric Spaces

PIAO Yong-jie,JIN Zhe-zhi

(College of Science,Yanbian University,Yanji133002,China)

A new unique common fxed point result for a pair of mappings satisfying certain quasi-Lipschitz type conditions on a topological vector space-valued cone metric space is obtained,and its particular forms and a more general form are given.Our main results generalize and improve some well-known recent results in the literature.

TVS-valued cone metric space;quasi-Lipschitz type condition;common fxed point

§1.Introduction and Preliminaries

Huang and Zhang[1]generalized the notion of metric space by replacing the set of real numbers by an order Banach space,defned a cone metric space and established some fxed point theorems for contractive type mapping in a normal cone metric space.Subsequently, several other authors in[2-8]studied the existence of common fxed point of mappings satisfying a contractive type condition in a normal or non-normal cone metric space.On the other hand, the authors in[9-10]introduced a class of topological vector space-valued cone metric space which is bigger than the space introduced by Huang and Zhang[1]and obtained some fxed point theorems for a mapping or common fxed point theorems for a pair of mappings.Subsequently, several authors discussed the existence problems of fxed point or common fxed point for a mapping or a pair of mappings in TVS-valued cone metric spaces[1114].

In this paper,we study some common fxed point theorems for a pair of mappings satisfying certain quasi-Lipschitz type conditions on a TVS-valued cone metric space and obtain a more general and important result.

Let(E,τ)be always a topological vector space(TVS)andP0a subset ofE.ThenP0is called a cone whenever

(i)P0is closed,nonempty andP0/={0};

(ii)ax+by∈P0for allx,y∈P0and for all nonnegative real numbersa,b;

(iii)P0∩(-P0)={0}.

For a given coneP0⊂E,we defne a partial ordering≤with respect toP0byx≤yif and only ify-x∈P0.x＜ystand forx≤yandx/=y,whilex≪ystand fory-x∈intP0, where intP0denotes the interior ofP0.

Defnition 1[9-10]LetXbe a nonempty set.Supposed:X×X→Esatisfes

(d1)0≤d(x,y)for allx,y∈Xandd(x,y)=0 if and only ifx=y;

(d2)d(x,y)=d(y,x)for allx,y∈X;

(d3)d(x,y)≤d(x,z)+d(z,y)for allx,z,y∈X.

Thendis called a topological vector space-valued cone metric onXand(X,d)is called a topological vector space-valued cone metric space(simply,TVS-valued cone metric space).

Defnition 2Let(X,d)be a TVS-valued cone metric space,x∈X,{xn}n∈N⊂X.

(i){xn}is a Cauchy sequence whenever for everyc∈Xwith 0≪c,there existsN∈N such thatd(xm,xn)≪cfor alln,m＞N;

(iii)(X,d)is called complete if every Cauchy sequence is convergent.

Lemma 1[10]Let(X,d)be a TVS-valued cone metric space,P0a cone subset of(E,τ),{xn}be a sequence inX,{an}a sequence inP0converging to0.Ifd(xn,xm)≤anfor everyn∈N withm＞n≥1,then{xn}is a Cauchy sequence.

§2.Main Results

Theorem 1Let(X,d)be a complete TVS-valued cone metric space,m,n∈N.Suppose that two mappingsS,T:X→Xsatisfy the quasi-Lipschitz type condition

whereA,B,C,D,Eare fve non-negative real functions onX×Xsatisfying the followingconditions

IfSmTn=TnSm=1X,thenSandThave a unique common fxed point,and for anyx0∈X, the sequence{xk}determined by=0,1,···converges to the unique common fxed point ofSandT.

ProofSinceandTnare all surjective mappings.Take any elementx0∈Xand construct a sequenceas follows

Fork=0,1,2,···,

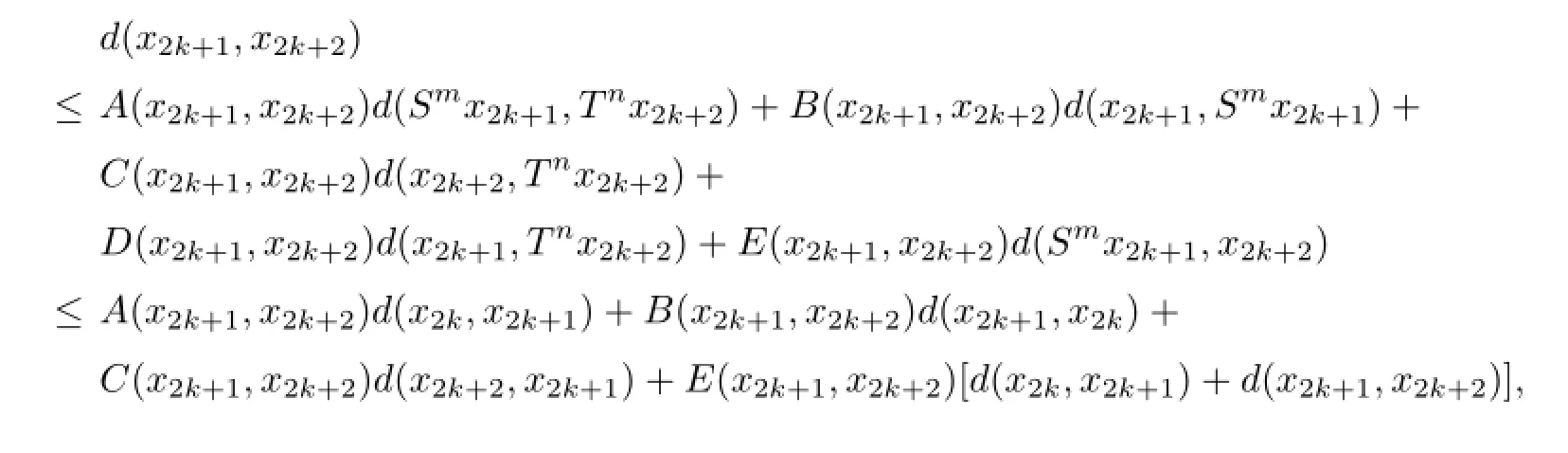
hence calculating and arranging the above,we have

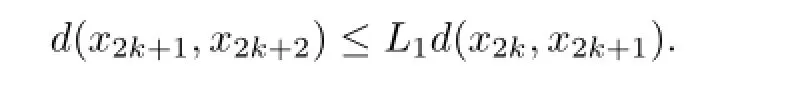
Similarly,

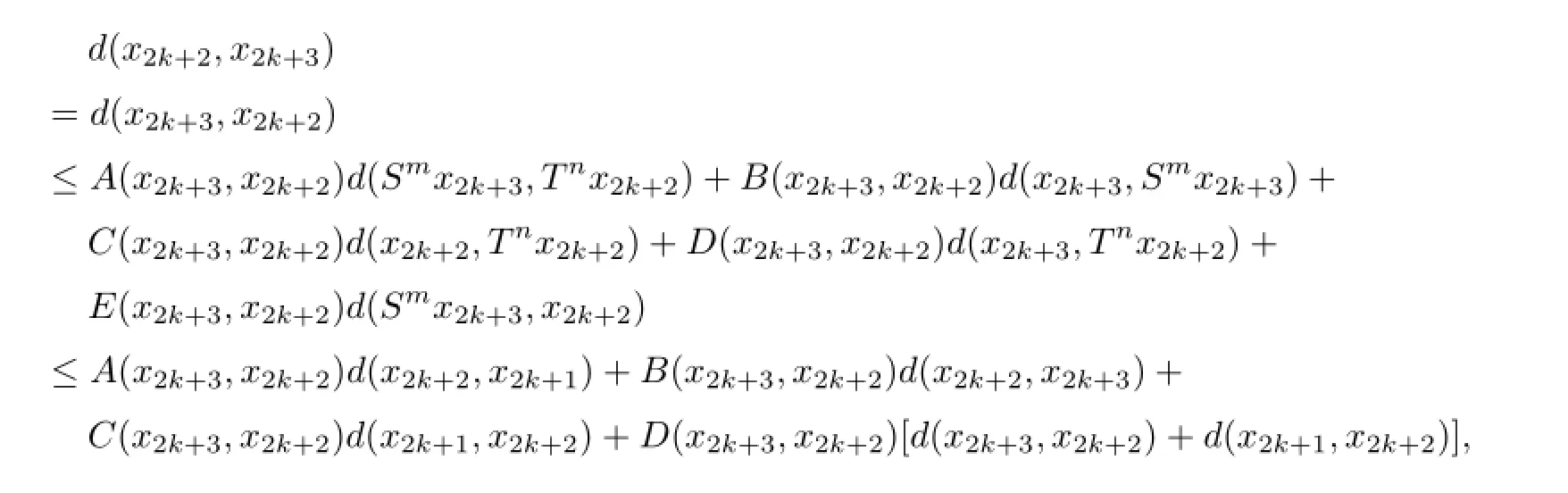
hence

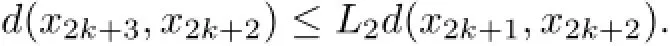
Applying mathematical induction,we obtain that for allk=0,1,2,···,

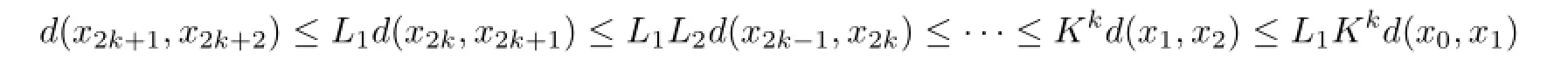
and

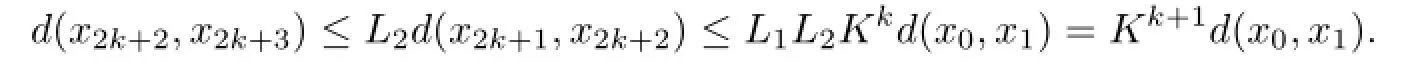
Forp,q∈N withp＜q,

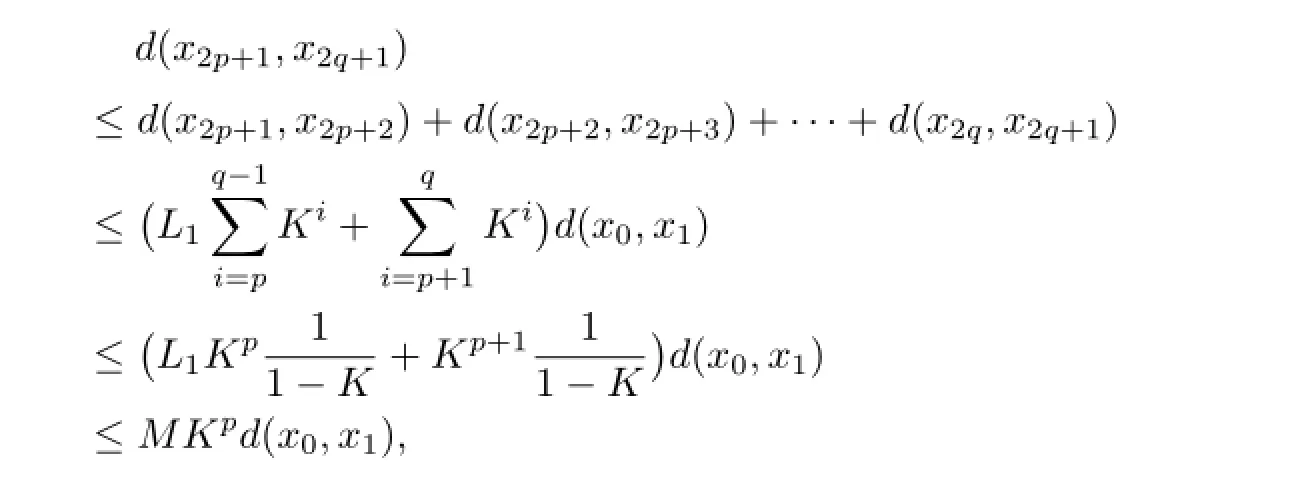
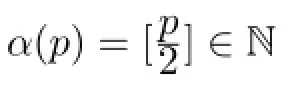
Letap=MKα(p)d(x0,x1),thenap∈P0for allp∈N andap→0 asp→∞because of 0≤K＜1.Hence{xk}is a Cauchy sequence by Lemma 1.Therefore there existsu∈Xsuch thatxk→uask→∞by the completeness ofX.

Next,we prove thatuis the unique common fxed point ofSandT.Since

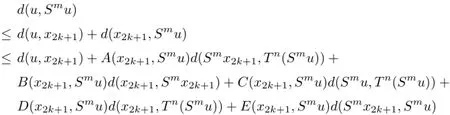
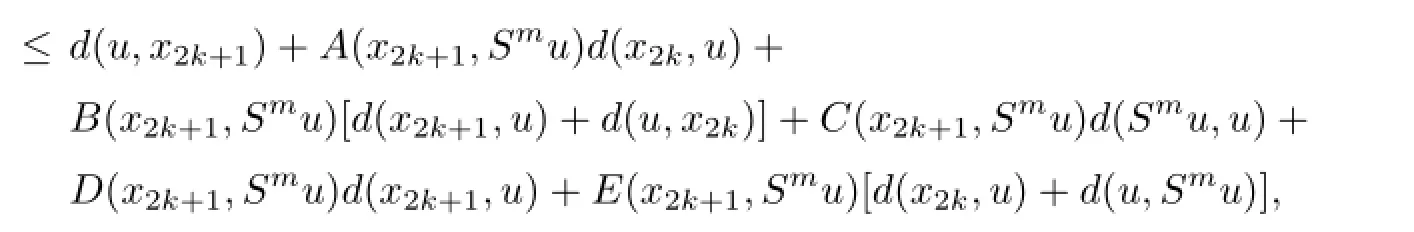
we have

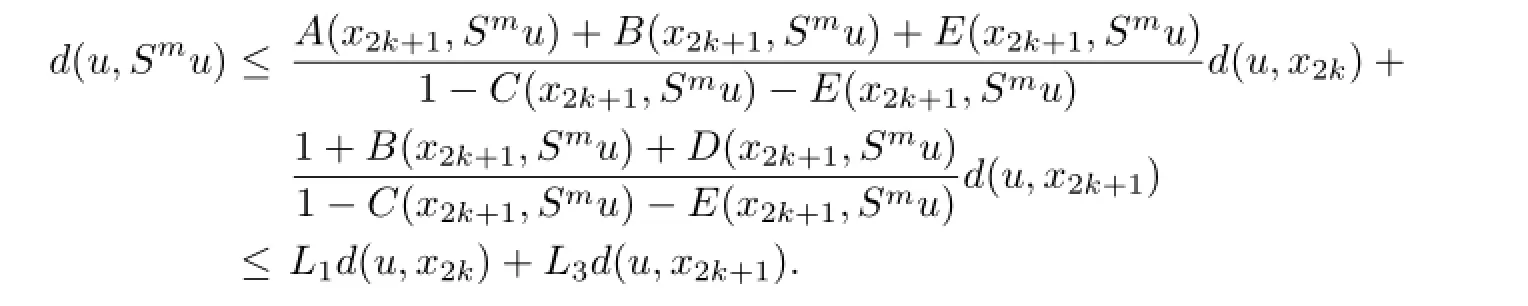
Sincexk→u,for any 0≪c,there existsN1such that fork＞N1,

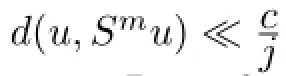
hence

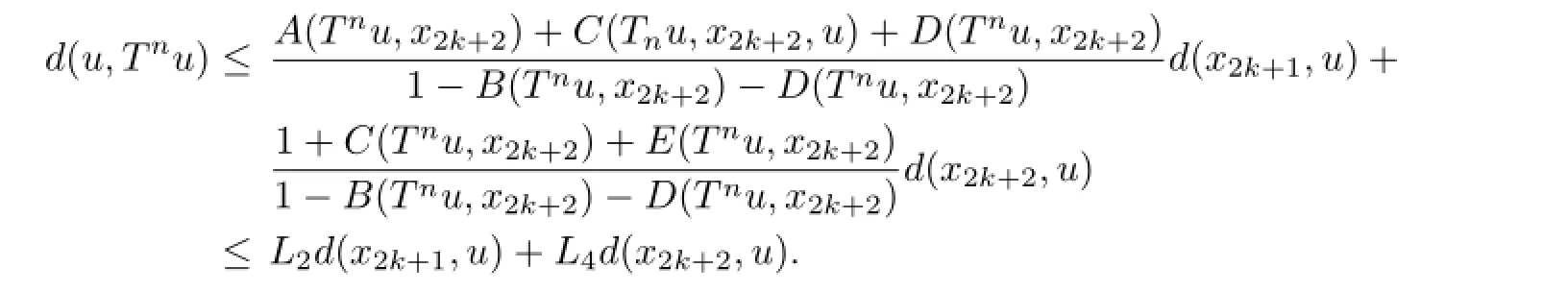
Therefore we can also obtain thatu=Tnu.Sou=Smu=Tnu.Since

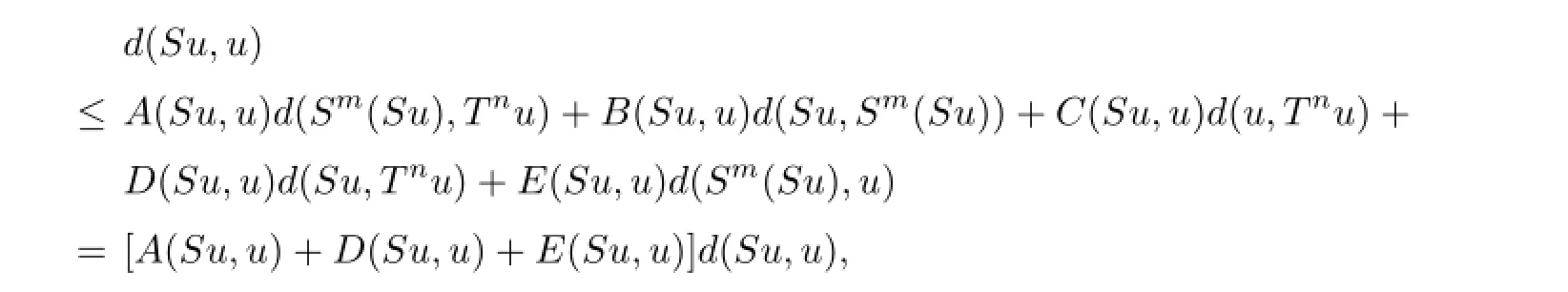
henced(Su,u)=0 due to[A(Su,u)+D(Su,u)+E(Su,u)]＜1,i.e.,Su=u.Similarly,

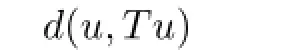
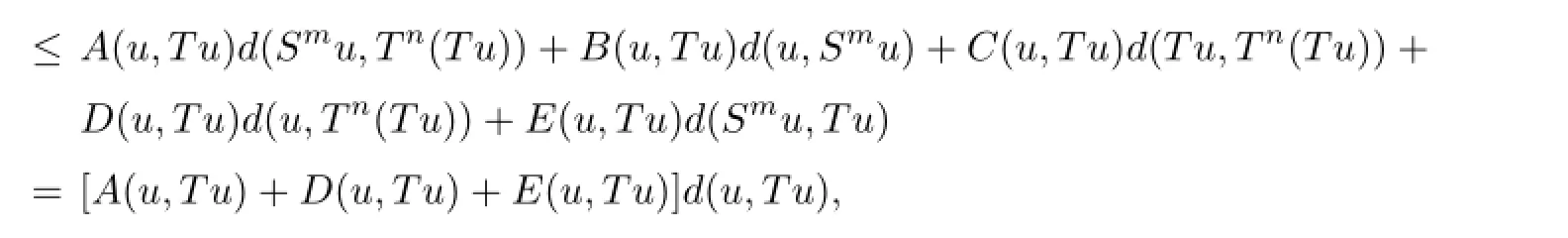
henceu=Tu.Thereforeuis the common fxed point ofSandT.

Ifu∗is also a common fxed point ofSandT,then

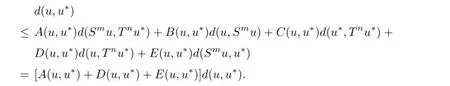
Henced(u,u∗)=0.Thereforeuis the unique common fxed point ofSandT.

Now,we give some particular forms of Theorem 1.

Theorem 2Let(X,d)be a complete TVS-valued cone metric space,m,n∈N.Suppose that two mappingsS,T:X→Xsatisfy the following quasi-Lipschitz type condition

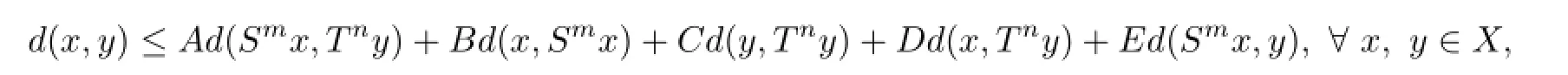
whereA,B,C,D,Eare fve non-negative real numbers satisfying that there exitsε＞0 such thatA+B+C+D+E=1+ε,A+D+E＜1,C+E＜1,B+D＜1,(C-B)(D-E)＞2ε. IfSmTn=TnSm=1X,thenSandThave a unique common fxed point.And for anyx0∈X, the sequence{xn}determined by=0,1,···converges to the unique common fxed point ofSandT.

ProofObviously,

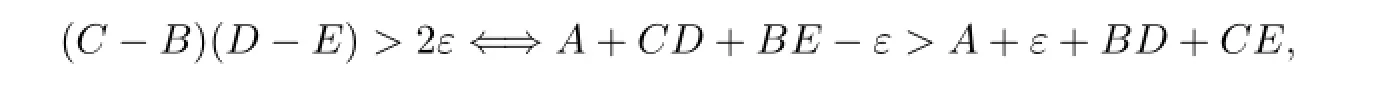
hence

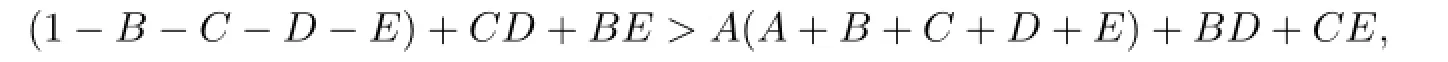
which implies that

ThereforeSandThave a unique common fxed point by Theorem 1.

Theorem 3The conditions ofA,B,C,D,Ein Theorem 2 can be replaced by the following conditions without changing its conclusionProofTakeε＞0 such that(C-B)(D-E)＞2εandA+D+E+ε＜1,and letA′=A+ε.Obviously,the following quasi-Lipschitz type condition holds

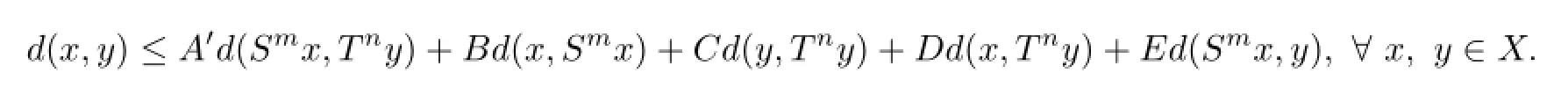
HenceA′,B,C,D,Esatisfy all conditions in Theorem 2,thereforeSandThave a unique common fxed point.

Theorem 4The conditions ofA,B,C,D,Ein Theorem 2 can be replaced by the following conditions without changing its conclusion

ProofThe inequalityA+B+C+D+E＜1 impliesA2+A(1-A)＜1-(B+C+D+E), hence

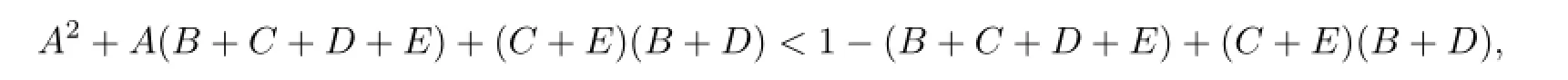
or

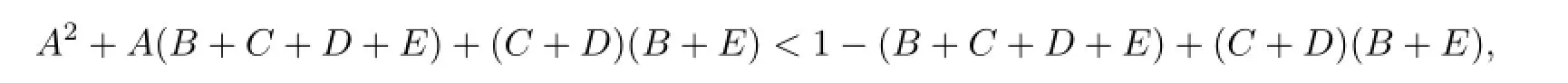
which implies that

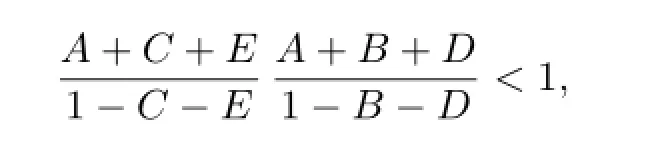
or

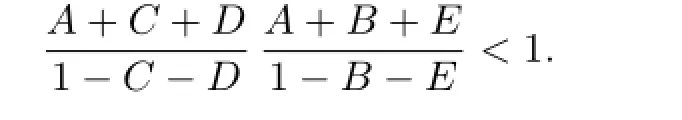
IfB=CorD=E,then the above two relations deduce that

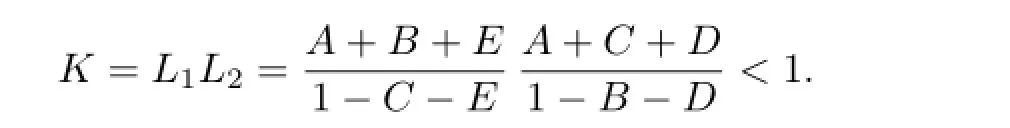
HenceSandThave a unique common fxed point by Theorem 1.

Theorem 5Let(X,d)be a complete TVS-valued cone metric space,m∈N.Suppose thatT:X→Xsatisfy the following quasi-Lipschitz type condition

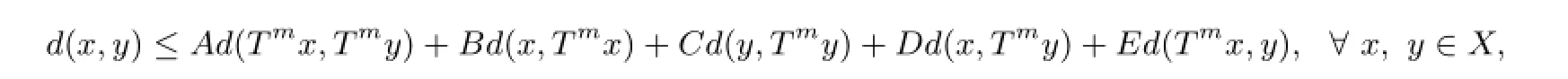
whereA,B,C,D,Eare fve non-negative real numbers such thatA+B+C+D+E＜1. IfT2m=1X,thenThas a unique fxed point.And for anyx0,the sequence{xn}determined byxk=Tmxk+1,k=0,1,···,converges the unique fxed point ofT.

ProofFrom the given quasi-Lipschitz type condition,we obtain

hence we obtain

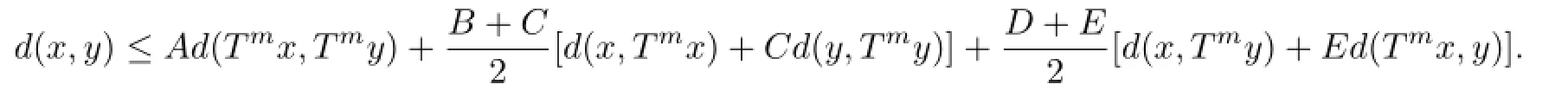
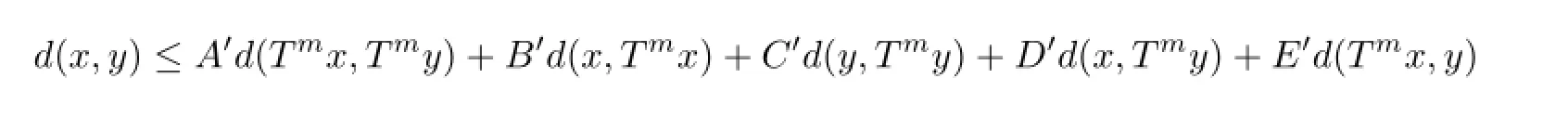
Finally,we discuss the existence problem of common fxed point for 2N-mappings.Theorem 6Let(X,d)be a complete TVS-valued cone metric spacefamilies of positive integers.Suppose that for eachi=1,2,···,N,two mappingsSi,Ti:X→Xsatisfy the following quasi-Lipschitz type condition

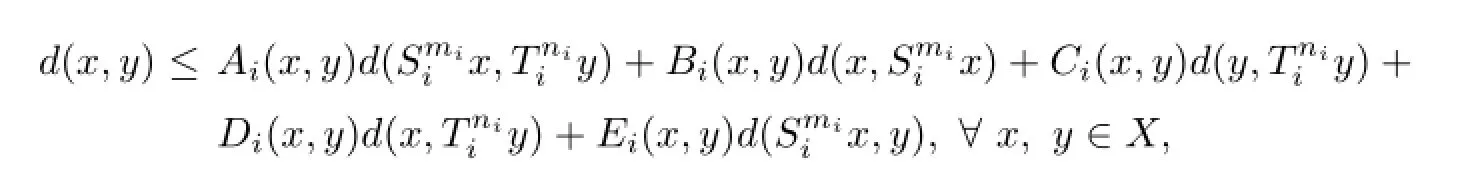
whereAi,Bi,Ci,Di,Eiare fve non-negative real functions onX×Xsatisfying

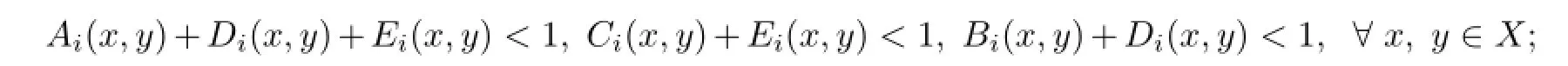
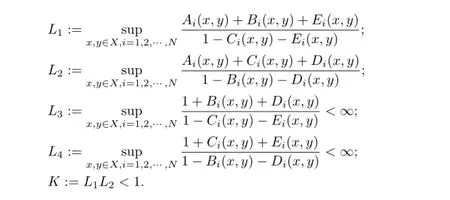
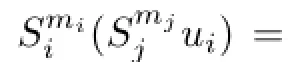
The uniqueness is obvious.

[References]

[1]HUANG Long-guang,ZHANG Xian.Cone metric spaces and fxed point theorems of contractive mappings[J].J Math Anal Appl,2007,332(2):1468-1476.

[2]ABBAS M,JUNGCK G.Common fxed point results for non-commuting mappings without continuity in cone metric spaces[J].J Math Anal Appl,2008,341(1):416-420.

[3]ABBAS M,RHOADES B E.Fixed and periodic point results in cone metric spaces[J].Applied Math Letters, 2009,22(4):511-515.

[4]RAJA P,VAEZPOUR S M.Some extensions of Banach’s contraction principle in complete cone metric spaces[J].Fixed Point Theory and Applications,2008,Article ID 768294.

[5]KADELBURG Z,RADENO´VIC S,ROSI´C B.Strict contractive conditions and common fxed point theorems in cone metric spaces[J].Fixed Point Theory and Applications,2009,Article ID 173838.

[6]JUNGCK G,RADENO´VCIC S,RADEJE´VIC S,et al.Common fxed point theorems for weakly compatible pairs on cone metric spaces[J].Fixed Point Theory and Applications,2009,Article ID 643840.

[7]ILI´C D,RAKO˘CEVI´C V.Quasi-contraction on a cone metric space[J].Applied Math Letters,2009,22(5): 728-731.

[8]HUANG Hua-ping,XU Shao-yuan,HAN Yan.Some fxed point results on a class of contractive mappings in cone metric spaces[J].Chin Quart J of Math,2013,28(4):539-545.

[9]BEG I,AZAM A,ARSHAD M.Common fxed points for mapps on topological vector space valued cone metric spaces[J].Inter J Math Math Sci,2009,doi:10.1155,ID 560264.

[10]AZAM A,BEG I,ARSHAD M.Fixed point in topological vector space valued cone metric spaces[J].Fixed Point Theory and Applications,2010,doi:10.1155,ID:604084.

[11]ABDLJAWED TH,KARAPINAR E.A common fxed point theoem of Gregus type on convex cone metric spaces[J].J Comput Anal Appl,2011,13:609-621.

[12]KARAPINAR E,YUKSEL U.On common fxed point theorem without commuting conditions in TVS-cone metric spaces[J].J Comput Anal Appl,2011,13:1123-1131.

[13]CHO Y J,SAADATI R,Wang Sheng-hua.Common fxed point theorems on generalized distance in order cone metric spaces[J].Comput Math Appl,2011,61:1254-1260.

[14]ABDLJAWED TH.Completions of TVS-cone metric spaces and some fxed point theorems[J].Gazi Univ J Sci,2011,24(2):135-240.

O189.1,O177.91

:A

1002–0462(2016)04–0390–09

Received date:2014-07-17

Foundation item:Supported by the National Natural Science Foundation of China(11361064)

Biographies:PIAO Yong-jie(1962-),male(chaoxianzu),native of Jiutai,Jilin,a professor of Yanbian University,Ph.D.,engages in nonlinear theory and fxed point theory;JIN Zhe-zhi(1977-),male(chaoxianzu),native of Mudanjiang,Heilongjiang,a lecturer of Yanbian University,Ph.D.,engages in fnancial mathematics

2000 MR Subject Classifcation:47H05,47H10,54E40