化简二次型方法的探讨

许 　 娟

(安庆师范学院 数学与计算科学学院, 安徽 安庆 246133)



化简二次型方法的探讨

许 娟

(安庆师范学院 数学与计算科学学院, 安徽 安庆 246133)

摘要：二次型是高等代数中非常重要的内容。化二次型为标准形是二次型教学中的重点与难点，除了线性替换法、矩阵法两个常用方法外，这里我们将给出从解析几何的角度出发的一种新方法，该方法简单、直观。

关键词：二次型；标准形；二次曲面；主径面

在高等代数的教学中，从行列式到矩阵做了很多的知识准备工作，用来处理后续的线性方程组解的结构、二次型化标准形、线性变换和若当标准形等问题。其中二次型的理论在微积分、力学、信号理论、计算机图形等学科中有很广泛的应用。如何化二次型为标准形非常重要，它有很强的直观解释，在3维空间里的几何解释实际上就是通过坐标系的旋转、平移，将原本含有交叉项的三元二次多项式化成只有平方项的多项式，如：

2xy-6yz+2xz⟹2u2-2v2+6w2

2xy-6yz+2xz=0⟹2u2-2v2+6w2=0

χχ

(不清楚什么几何图形)(二次锥面，如图1)

因此，将二次型化成标准形有助于我们对多元二次方程的几何图形的直观想象(什么样的曲线？什么样的曲面？)。今天，我们倒过来，从几何角度出发，给出一种新的求二次型标准形的方法。

1二次型标准形的求法

定义1[1]设P是一个数域，一个系数在数域P中的二次齐次多项式：

(1)

称为数域P上的一个n元二次型，二次型的矩阵为：

(2)

定义2设P是一个数域，一个系数在数域P中的二次方程：

2a1x1+2a2x2+…+2anxn+a=0

(3)

称为二次曲面的方程。特别的，

(4)

称为数域P上的二次型的方程。

一般的，在高等代数这门基础课的教学中，我们化简二次型为标准形的方法只给出了两种：线性替换法、矩阵法。由于在解析几何这门基础课中我们也没有讲授到一般二次曲面的研究与二次型的联系，所以忽视了一种新的方法。下面我们就这三种方法做个介绍，给出例题，比较各自优势，以后在处理这类问题的时候，可以选择计算量偏小的方法。

定理1[1]数域P上的二次型都可以经过非退化的线性替换变成平方和的形式。

线性替换法如下：

1)若ai i(i=1,2,…,n)中至少有一个不为零，不失一般性，设a11≠0，令

2)若所有ai i=0(i=1,2,…,n)，但至少有一a1j≠0(j>1)，不失一般性，设a12≠0，令

这也是一个非退化线性替换，使(1)变成：

继续1)的步棸，直到全变成平方项。

定理2[1]在数域P上，任意一个对称矩阵都合同于一对角矩阵。

矩阵法如下，

1)若ai i(i=1,2,…,n)中至少有一个不为零，例如a11≠0，令

递推下去，直到全部变成平方项；

2)若a11=0，但有一个ai i≠0，作

P(1,i)AP(1,i)，归结到情形1)；

3)若所有ai i=0(i=1,2,…,n)，但至少有一a1j≠0(j>1)，不失一般性设a12≠0，作

P(2,j)′AP(2,j)，然后取

于是又归结到情形1)。

例1化二次型f(x1,x2,x3)=2x1x2-6x2x3+2x1x3成标准形。

解(线性替换法)作非退化线性替换：

注实际上方程2x1x2-6x2x3+2x1x3=0的几何图形就是一锥面。

下面将给出利用坐标变换的方法去化二次型为标准形，首先给出预备知识。三维空间一般坐标变换公式可由新坐标系的三个坐标面来确定(能够推广到n维)，设有两两垂直的平面(如下)分别为新坐标系的三个坐标面：

π1∶A1x+B1y+C1z+D1=0(y′O′z′面)

π2∶A2x+B2y+C2z+D2=0(z′O′x′面)

π3∶A3x+B3y+C3z+D3=0(x′O′y′面)

根据点的坐标与点到面的距离的关系，有如下坐标变换公式[2]：

为使右手系变成右手系，正负号的选择保证系数行列式的值为正即可。

定义3[2]二次曲面的一族平行弦的中点轨迹叫做共轭于这族平行弦的径面，垂直于共轭弦的径面叫做二次曲面的主径面。

性质1[2]主径面就是二次曲面的对称面。

基于这些知识，二次型的方程实际上是二次曲面方程中一次项及常数项全为零的特例，实际上如果找到二次曲面的三个主径面，以此为新坐标系，那么在这个坐标系下二次曲面的方程将特别的简单。有学者将一般二次曲面的方程归结为5种形式，曲面形状也只有17种[2]。因此只要将方程化成标准形，图形形状也就一目了然。下面通过例题给出具体操作过程。

例2化二次型f(x1,x2,x3)=x2+y2+5z2-6xy-2xz+2yz为标准形。

解先考察二次型的方程：x2+y2+5z2-6xy-2xz+2yz=0，因为I1=7,I2=0,I3=-36,所以它的特征根为λ1=6,λ2=3,λ3=-2，则分别有：

1)与λ1=6对应的主径面为-x+y+2z=0；

2)与λ2=3对应的主径面为x-y+z-9=0；

3)与λ3=-2对应的主径面为x+y=0。

取这三个主径面作为新坐标系的三个坐标面，则坐标变换为

得到二次曲面的简化方程：6x′2+3y′2-2z′2=0，即有原二次型的标准形为

6x′2+3y′2-2z′2

2二次型的应用

二次型的应用[4-7]很广泛，在不等式的证明、求极值、因式分解等方面均有应用。这里我们通过几个例题并利用前面介绍的三种化二次型为标准形的方法，展示二次型在这些方面的应用。

定理3[3]实二次型可以分解成两个实系数的一次齐次多项式乘积的充要条件是它的秩为2和符号差为0，或者秩等于1。

例3证明Cauchy不等式：

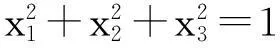
g=(y1+2y2)(y1-2y2)=

(x1+x2+2x3)(x1-3x3)

且f=g(x1,x2,x3)=(x1+x2+2)(x1-3x3)。

3结束语

通过几年基础课的教学，在讲授二次型和二次曲面这两章知识的同时，找到二者之间的一定联系，给出了一种通过主径面的知识求二次型标准形的方法，并且二次型还有很广泛的应用，它在不等式的证明、求最值、分解因式、求积分等方面均用利用价值。同时，希望学者可以结合几何直观去讲授代数知识，既增加了学生的空间想象能力，又促进了代数知识的学习，相得益彰。

参考文献:

[1] 北京大学数学系前代数小组.高等代数(第四版)[M]. 北京：高等教育出版社, 2013.

[2] 吕林根,许子道.解析几何(第四版)[M]. 北京：高等教育出版社, 2006.

[3] 丘维声.高等代数[M]. 北京：科学出版社, 2013.

[4] 王萼芳,石生明.高等代数辅导与习题解答[M]. 北京：高等教育出版社, 2007.

[5] Steve Roman. Advanced linear algebra[M]. 北京：世界图书出版公司, 2008.

[6] 沈灏,沈佳辰，译.线性代数及其应用[M]. 北京：人民邮电出版社,2010.

[7] 俞正光,鲁自群,林润亮.线性代数与几何[M]. 北京：清华大学出版社,2008.

Discussion on the Simplification Method of Quadric Form

XU Juan

(Department of Mathematics，Anqing Teachers College，Anqing 246133，China)

Abstract:Quadratic form is an very important content in advanced algebra. How to simplify quadratic form to standard form is important and difficult in teaching. In addition to the linear replacement method and the matrix method, we will present a new approach the analytic geometry angle. The method is simple and intuitive.

Key words:quadratic form, standard form, quadratic surface, principal radial plane

中图分类号：O231.9

文献标识码：A

文章编号：1007-4260(2015)01-0109-03

DOI：10.13757/j.cnki.cn34-1150/n.2015.01.031

作者简介：许娟，女，安徽和县人，硕士，安庆师范学院数学与计算科学学院讲师，研究方向为数字图像处理。

收稿日期：2014-06-28