二次曲面GPS高程拟合模型精度研究
2018-11-06黄中德
黄中德
摘要:针对二次曲面GPS高程转换模型精度问题,通过实验分别研究了测区大小、控制点分布和控制点数量对于高程拟合精度的影响。文中以两个大小不同的测区为研究对象,计算了控制点包围整个测区、分布在测区一角、均匀分布三个不同分布情况和控制点为6、7、8不同个数情况下的模型转换精度。实验结果表明,测区越小、控制点分布越均匀、已知点个数越多,二次曲面高程拟合模型精度就越高。
关键词:GPS;高程拟合;二次曲面;模型精度
引言
在当前的测绘生产活动中,由于定位速度快、定位精度高的优势,GPS已经成为一种非常重要的定位技术手段。在使用GPS进行定位时,由于GPS所测点的高程属于大地高,而我国在外业生产时用的是正常高,二者所选的高程参考面不一样,所以需要将GPS所测的大地高转换成正常高。常用的GPS高程转换方法有解析内插法、曲面拟合法、多面函数法、加权均值法、神经网络法等。二次曲面GPS高程拟合模型由于模型简单、计算方便等优势,成为GPS高程转换方法中一种使用广泛的高程拟合模型。本文结合两个不同测区的生產数据,通过实验的方法,分别研究了测区大小、已知点分布和控制点数量对二次曲面高程拟合模型精度的影响,研究成果可以为工程应用提供一些参考。
1.二次曲面GPS高程拟合模型
1.1二次曲面拟合模型原理
模型基本原理:根据测区中已知点的平面坐标x,y和高程异常ξ值,用数值法拟合,拟合出测区似大地水准面,再内插出待求点的ξ,把GPS直接测得的大地高减去求得的高程异常值,即可求出待求点的正常高。设点的高程异常值ξ与平面坐标x,y有以下关系:
对于测区内任意一个点,利用求解的系数矩阵B,只要将点的平面坐标x,y代人公式(1)中,即可计算出待求点的高程异常值ξ,进而就可以完成高程转换。
1.2模型精度评定
(1)内符合精度
式中:n为参与计算的已知点个数。
(2)外符合精度
式中:m为检核点的个数。
2.工程案例数据实验
2.1测区一
2.1.1测区一概况
引用参考文献中的数据,测区为云南某地区c级GPS控制网,整个测区面积约2500km2,测区中总共有24个GPS控制点,控制点全部为三等水准点,点位分布如图1所示。
2.1.2模型转换精度研究
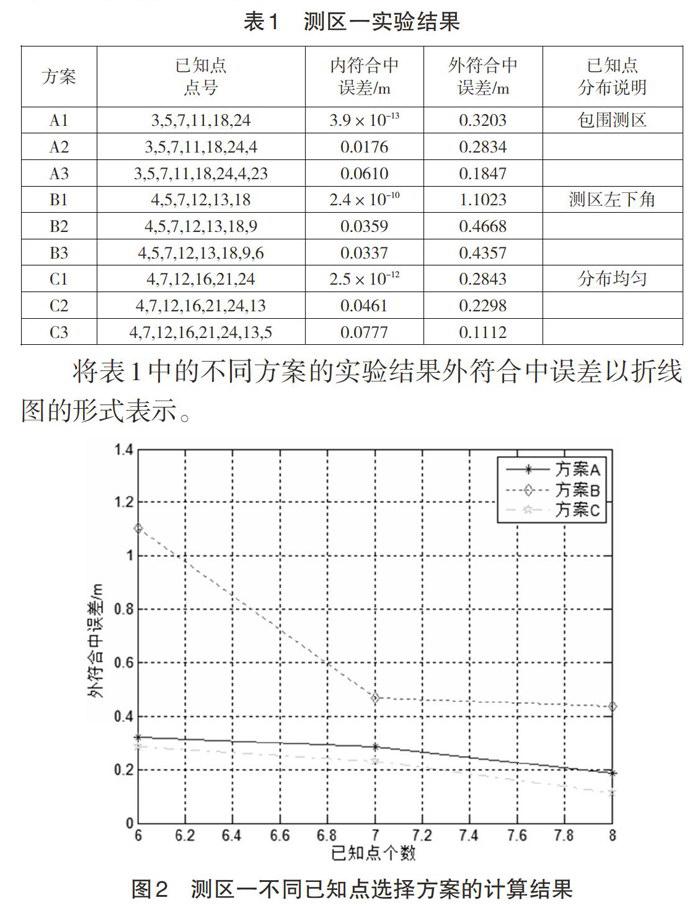
实验选取在测区分布相对均匀的1号、8号、10号和19号控制点作为检核点,从剩下的20个控制点中,按照不同的控制点个数和控制点分布情况确定不同的已知点选择方案,分别进行实验计算,实验结果如表1所示。
将表1中的不同方案的实验结果外符合中误差以折线图的形式表示。
从测区一的实验结果可以看出:在控制点分布相同的情况下,控制点个数越多,模型精度就越高;在控制点个数相同的情况下,控制点分布越均匀,模型精度就越高。
2.2测区二
2.2.1测区二概况
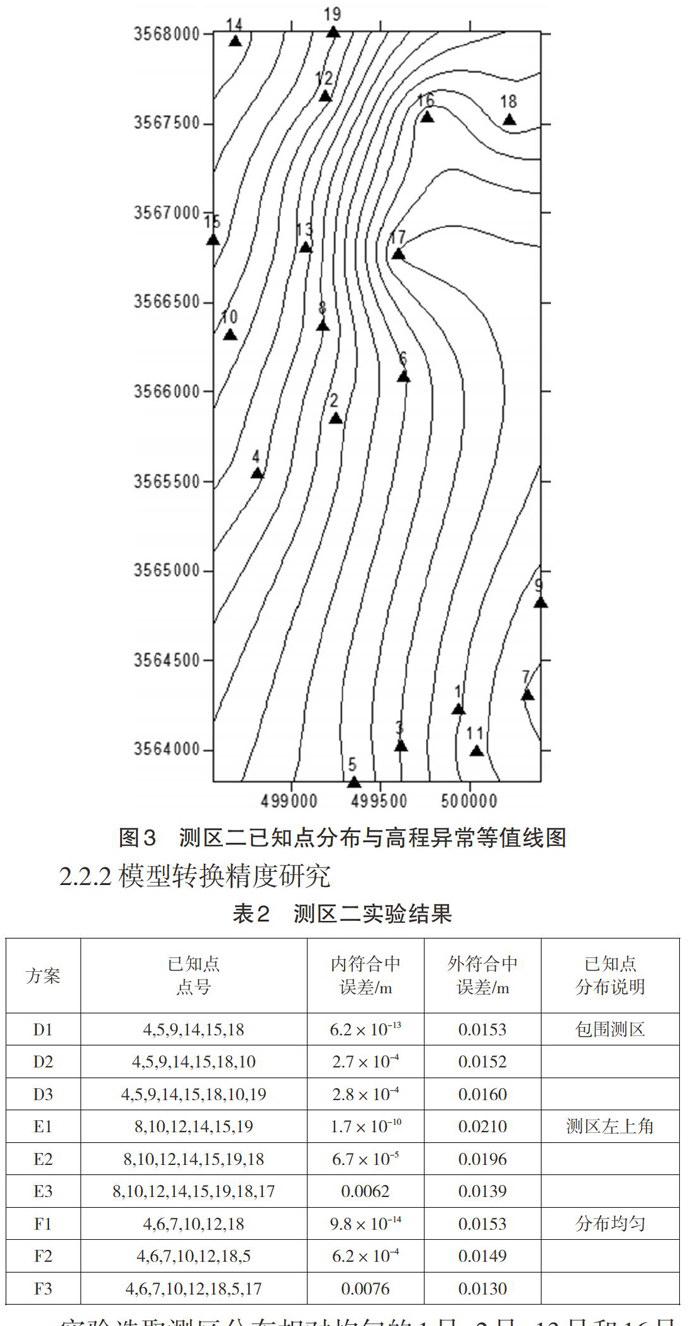
引用参考文献中的数据,测区为某沿江地形平缓区的控制网,平均边长约1km,区域面积约为10km2,按国家B网级要求施测。GPS网共19个点,所有控制点都进行了二等水准联测点位分布如图3所示。
2.2.2模型转换精度研究
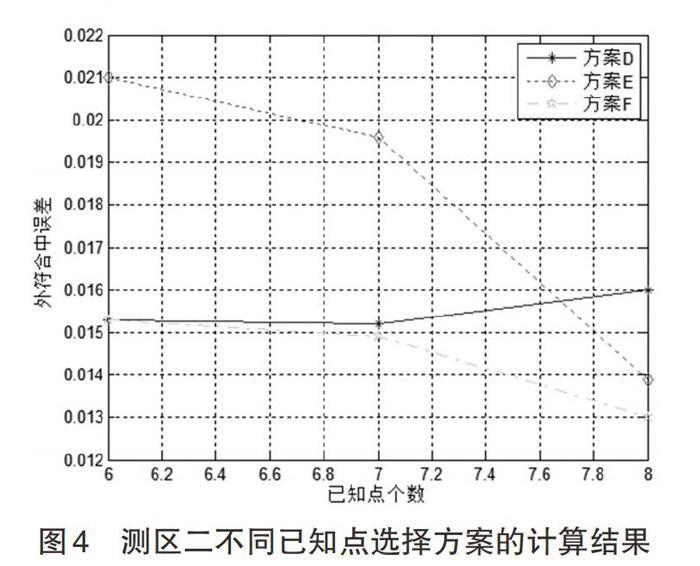
实验选取测区分布相对均匀的1号、2号、13号和16号控制点作为检核点,从剩下的15个控制点中,按照不同的控制点个数和控制点分布情况确定不同的已知点选择方案,分别进行实验计算,实验结果如表2所示。
将表2中的不同方案的实验结果外符合中误差以折线图的形式表示。
从测区二的实验结果可以看出:在控制点分布相同的情况下,控制点个数越多,模型精度就越高;在控制点个数相同的情况下,控制点分布越均匀,模型精度就越高。
结论
通过对以上两个测区的实验数据进行分析,可以得出以下结论:
(1)在控制点个数相同的情况下,控制点的分布情况决定了二次曲面拟合模型的精度,控制点分布越均匀,模型的拟合精度就越高。
(2)在控制点分布情况相似的情况下,适当增加控制点的个数,模型的精度会有所提高,测区越大,精度提高的效果就越明显。
(3)在控制点个数和分布情况相同的情况下,测区的大小影响了二次曲面拟合模型的精度,测区越大,模型的拟合精度就越低。
上述实验结论是根据两个测区的数据得出的,实验结果并未考虑地形起伏和控制点精度的影响,只是将来需要更进一步深入研究的问题。