裂纹尖端附近应力场和位移场精确解分析

薛建阳，董金爽，尚 鹏

（西安建筑科技大学土木工程学院， 陕西 西安 710055）

断裂力学中将裂纹分为I型、II型和III型三类，又称为张开型(拉伸型)、滑开型(剪切型)和撕开型．当裂纹尖端的极坐标系中极半径r趋于零应力场、应变场和位移场都称为近场，即裂纹尖端附近[1]．裂纹尖端附近存在应力集中，通常根据Saint-Venant原理采用局部解对裂纹问题进行分析，即用近似解代替精确解，这种情况下得到的近似解存在一定的局限性．目前，在确定裂纹尖端附近相关物理量时，如应力强度因子，常基于Irwin理论进行计算．董国兴[2]分析了 Irwin公式成立条件，得出仅当r≤a(a为裂纹长度)时，用近似解代替精确解才能满足精度要求．但实际情况是对离裂纹尖端具有一定距离的点进行测量或试验时，一般较难满足r≤a，若用所得结果确定裂纹尖端的应力强度因子，或只有在满足r≤a才能得到准确值的物理量时，则会引起较大误差，甚至产生错误的结果[3]．因此确定近似解的工程适用范围及裂纹尖端应力场和位移场的精确解是十分必要．

胡卫华[4]根据 Muskhelishvili应力函数法推导出了I型裂纹尖端附近应力场的精确解，并与近似解进行了误差分析．王燮山[5]利用正交曲线坐标和ΓοЛοсοв复势函数推导出了无限大平板I型、II型裂纹尖端应力场及位移场的精确解，提出了适用于求解场内任意点位移和应力的公式．杨槐堂[3]采用Westergaard函数法推导出了沿着θ=0°及θ=π/2方向上无限大平板在裂纹尖端附近应力场和位移场的特殊解，同时克服了r≤a限制条件．

通过分析发现，有关裂纹尖端应力场和位移场精确解分析的研究还较缺乏．因此，本文采用Westergaard函数法基本原理对裂纹尖端应力场和位移场精确解进行研究，推导出其在任意角度方向上的数学表达式，该方法即能克服r≤a限制条件扩大其适用范围的同时还能提高计算精度，最后取θ=π/6作为算例加以说明．

1 基本理论

断裂力学中，Irwin应用Westergaard函数的方法分析了裂纹问题，从而将含裂纹的线弹性体的线弹性力学归结为弹性力学平面问题进行分析，实际上是寻找一个满足边界条件及双调和方程的应力函数，该应力函数实际上是复变应力函数．具有穿透裂纹作用有无限远处的均匀应力的无限大平板，其复变应力函数Z的具体表达形式如式(1)示[6]：

线弹性断裂力学中平面裂纹，当受到 I型、II型和 III型任一种或两种以上荷载作用，裂纹尖端附近应力场和位移场表达式如式(2)、式(3)所示[6]：

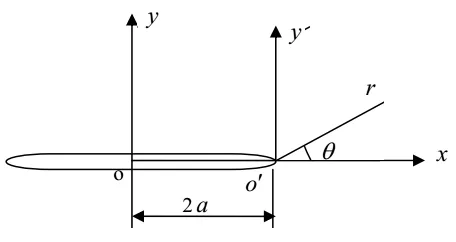
图1 裂纹的对应坐标及变换Fig.1 Coordinates and transformation of the crack

其中：z=x+iy，如图1所示．

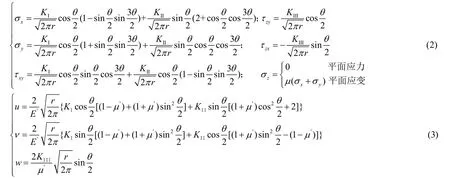
式中：E´，μ´分别为材料的弹性模量和泊松比．

裂纹尖端应力场和位移场数学表达式分别为 I型裂纹应力场与位移场：

II型裂纹应力场与位移场：

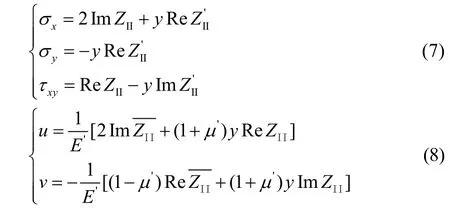
III型裂纹应力场与位移场：

式中：E´，μ´分别为材料的弹性模量和泊松比．

2 裂纹尖端应力场位移场精确解推导

根据断裂力学，三种类型裂纹的应力场和位移场仅与复变应力函数 Z本身及其导数和积分有关．将坐标原点由裂纹中心平移至裂纹右尖端处，采用新坐标系xo´y´，新坐标ξ，如图1所示．

由式(1)知，三种类型裂纹复变应力函数Z具有相同表述形式，仅应力σ，τ，τ´的差异，因此以 I型裂纹为例计算Z的导数和积分表达式．

对复变应力函数Z求导和求积分可得：

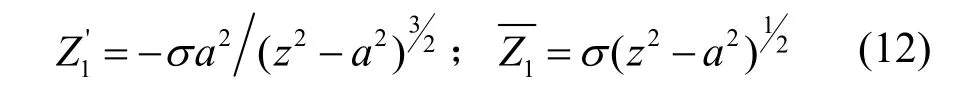
将式(11)进行变换可得：

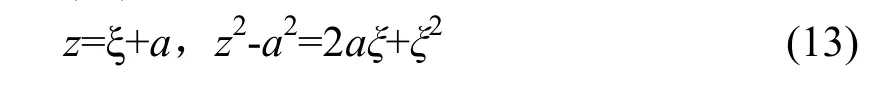
将式(13)代入到式(1)可得：

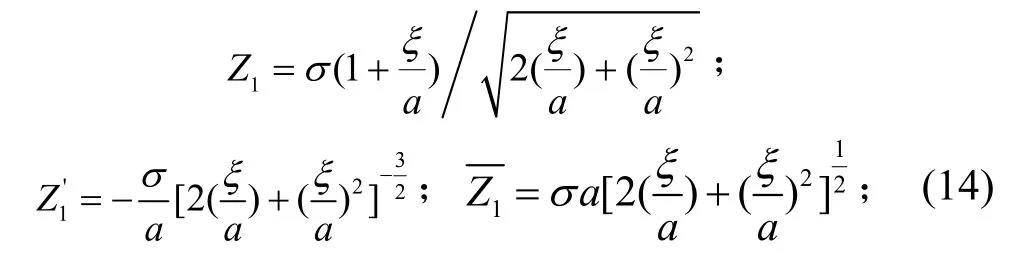
根据欧拉公式对式(11)变换得

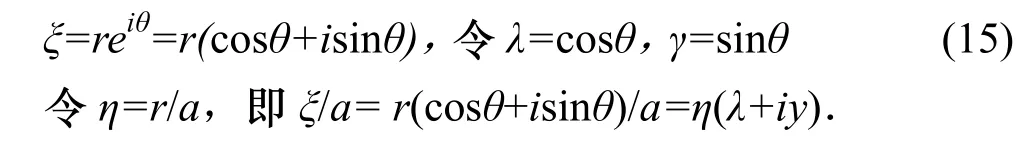
将式(15)代入式(14)，经计算得：

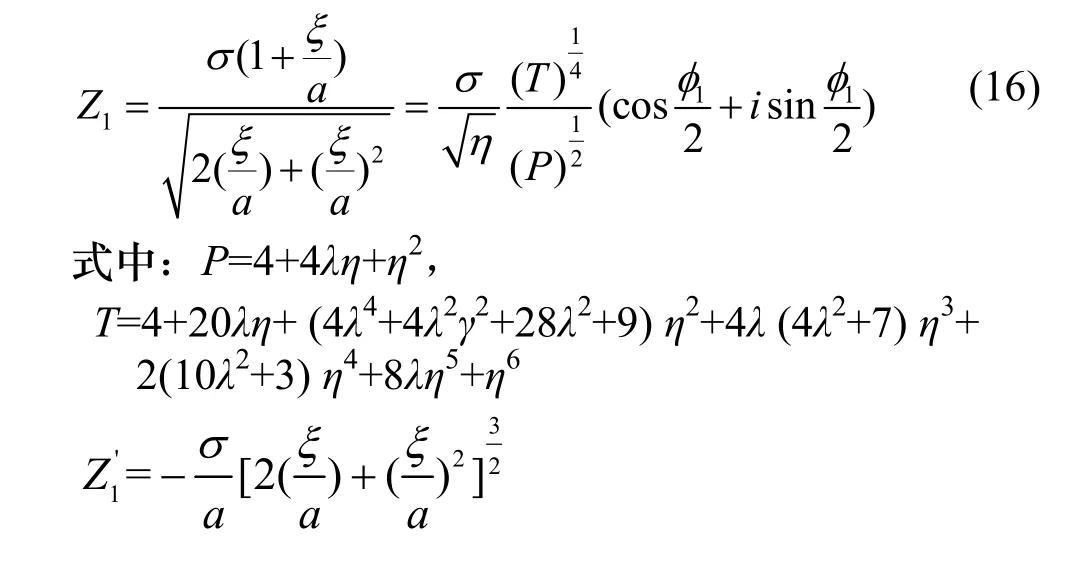
将式(16)-(18)分别代入式(5)-(10)便可得 3种类型裂纹尖端附近应力场和位移场的精确解表达式．

本文所推导公式适用于裂纹尖端附近应力场与位移场沿任意角度方向精确解．文中将以θ=π/6为例，对I型、II型、III型三种不同形式裂纹尖端附近应力场与位移场精确解进行计算分析．对于裂纹尖端附近应力场和位移场沿θ=0°与θ=90°方向的精确解按照本文中所推导公式计算，可得出与文献[3]一致的结果，限于篇幅，在此不再赘述．

3 裂纹尖端应力场精确解算例分析(θ=π/6)

将θ=π/6代入到式(16)-(18)，分别得数学表达式．

将θ=π/6代入式(2)得裂纹尖端附近应力场近似解．对含有中心裂纹无限大平板的应力强度因子表达式为将式(19)-(21)分别代入式(5)、式(7)、式(9)得 I型、II型、III型裂纹尖端应力场的精确解．

当θ=π/6 时，y=rsinθ=r/2．

3.1 I型裂纹

定义修正系数为裂纹尖端附近应力场(位移场)精确解与近似解的比值．

I型裂纹尖端附近应力场修正系数，如式(22)．

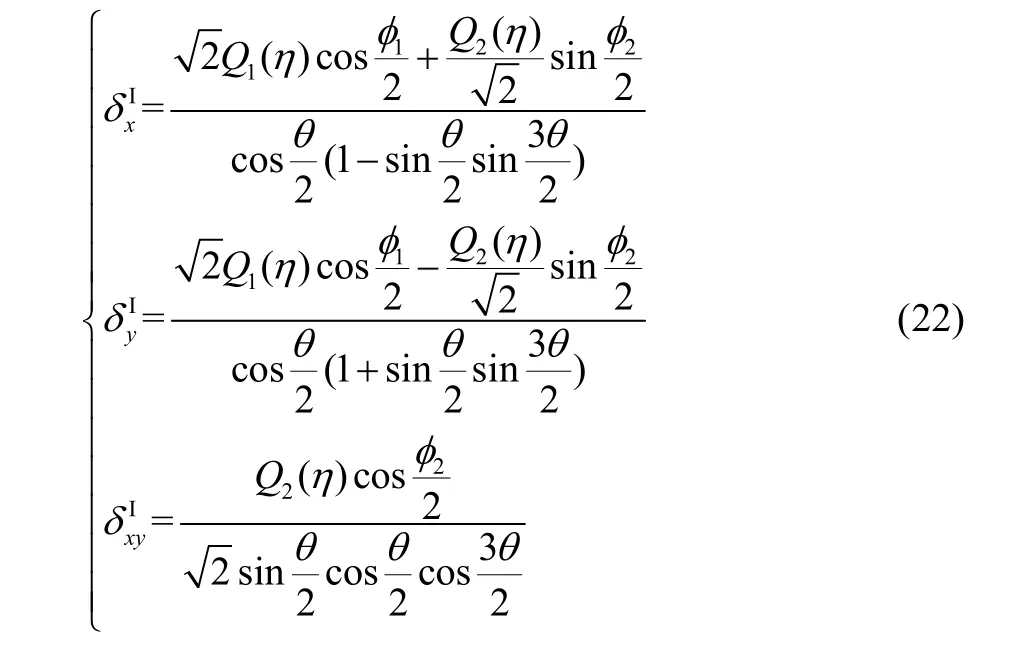
对式(22)取不同η值，其数值结果如图2所示．

图2 I型裂纹应力场修正系数Fig.2 Revision factors of the stress field for I-type crack

当η=r/a≤0.8时，系数拟合公式如式(23)所示：

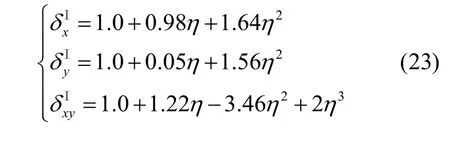
3.2 II型裂纹

II型裂纹尖端附近应力场修正系数，如式(24)．

对式(24)取不同η值，其数值结果如图3所示．

图3 II型裂纹应力场修正系数Fig.3 Revision factors of the stress field for II-type crack

当η=r/a≤0.8时，系数拟合公式如式(25)所示：

3.3 III型裂纹

III型裂纹尖端附近应力场修正系数，如式(26)．

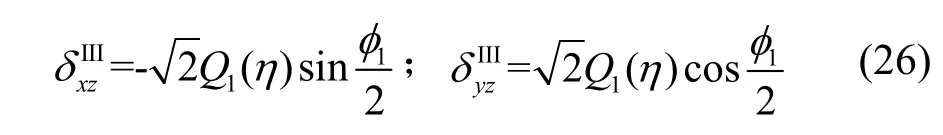
对式(26)取不同η值，其数值结果如图4所示．

从图2、图3、图4可知：

（1）随着离裂纹尖端距离的不断增加，裂纹尖

图4 III型裂纹应力场修正系数Fig.4 Revision factors of the stress field for III-type crack

当η=r/a≤0.8时，系数拟合公式如式(27)所示：

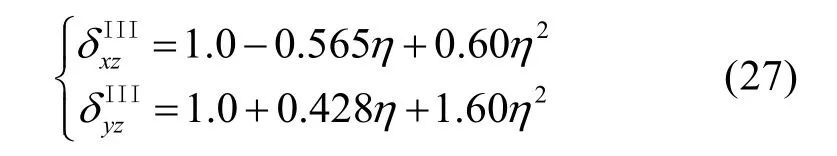
端应力近似解不断远离精确解，尤其是当η=r/a≤0.6时，两者最大可相差2.22倍．因此用距裂纹一定距离的应力近似解去确定材料的应力强度因子及其他相关物理量，则会引起较大的误差；

（2）当η=r/a≤1.0时，裂纹尖端附近的近似解与精确解相差较小，此时可以用近似解代替精确解，才不会引起较大误差；

（3）可以通过计算近似解与对近似解的修正系数δ，从而不需要繁琐的计算就可以确定距离裂纹尖端一定距离处的精确应力场．

4 裂纹尖端位移场算例分析(θ=π/6)

将θ=π/6代入式(3)，得到裂纹尖端位移场的近似解．将式(16)-(18)分别代入式(6)、式(8)、式(10)得到I型、II型、III型裂纹尖端位移场的精确值．

当θ=π/6 时，y=rsinθ=r/2．

4.1 I型裂纹

I型裂纹尖端附近位移场修正系数，如式(28)．

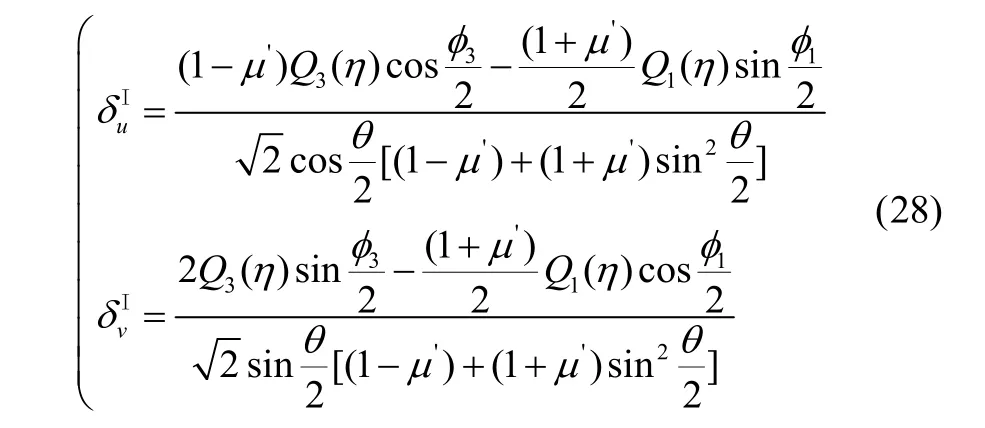
将式(4)代入式(28)得平面应变状态修正系数．

当η=r/a≤0.8时，系数拟合公式具体表达式如式(29)示：

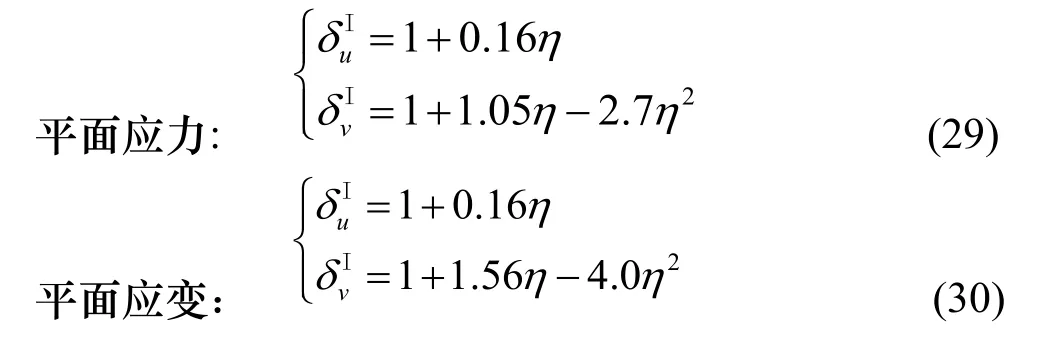
4.2 II型裂纹

II型裂纹尖端附近位移场修正系数，如式(31)．

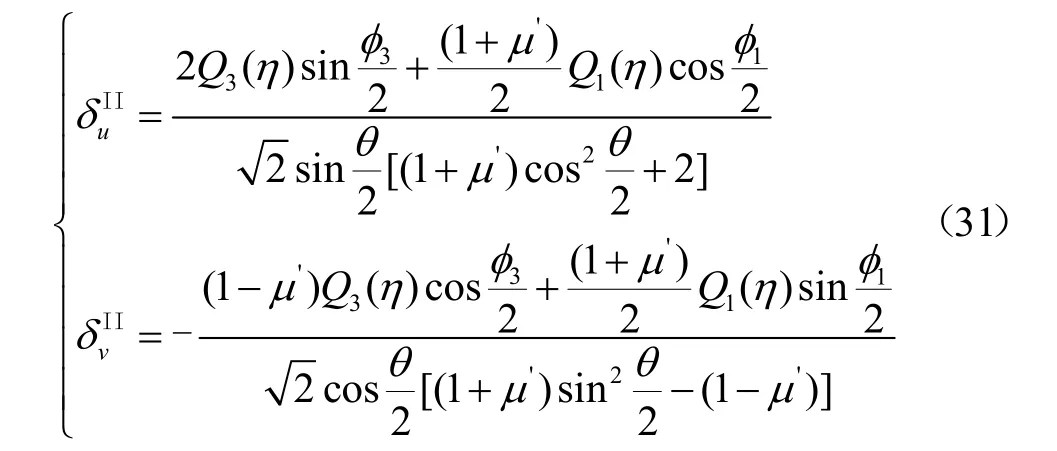
将式(4)代入式(31)可得平面应变状态下的修正系数．

当η=r/a≤0.8时，在平面应力和平面应变两种状态下曲线几乎重合，因此拟合公式可以采用相同的表达形式，如式(32)所示．

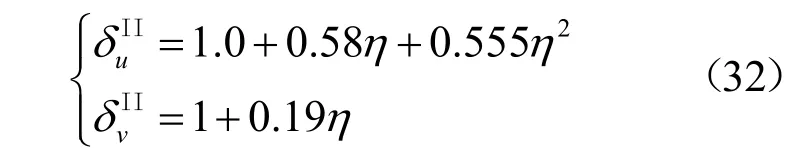
4.3 III型裂纹

III型裂纹尖端附近位移场修正系数，如式(33)．

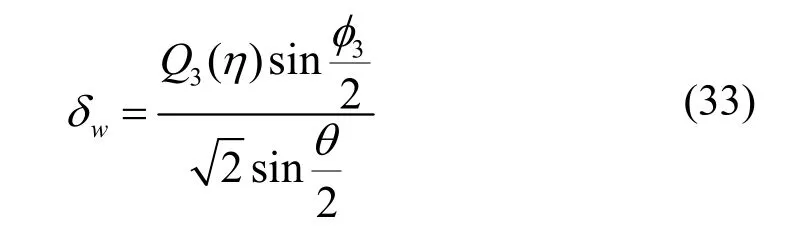
当η=r/a≤0.8时，可用式(34)拟合．

三种类型裂纹位移场近似解修正系数见表1．

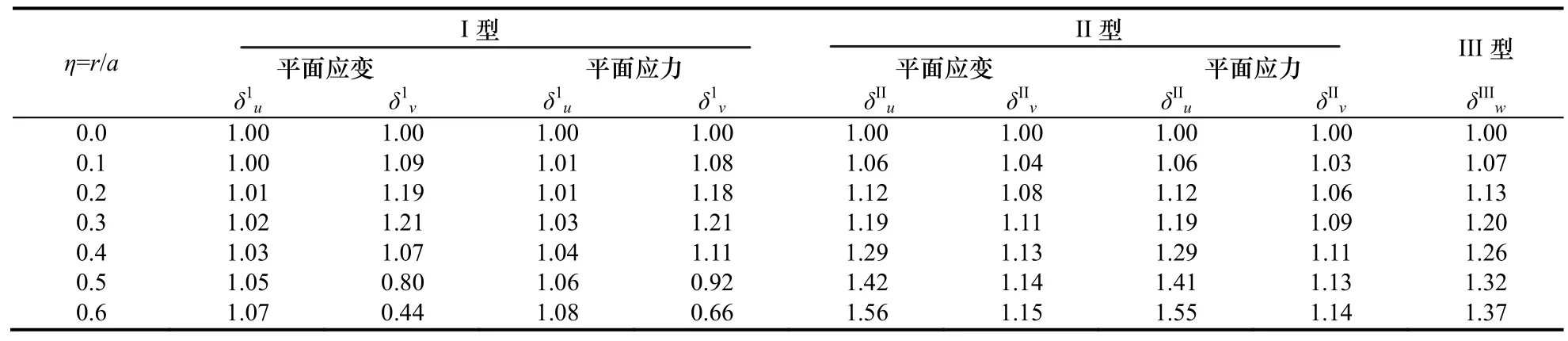
表1 θ=π/6时三种不同裂纹尖端附近位移场修正系数Tab.1 Revision factors of tip displacement field for three different cracks as θ=π/6

从表1可知：

（1）裂纹尖端附近位移场的近似解与精确解随着远离裂纹尖端的距离而不断远离，尤其是η=r/a≤0.5时，两者最大相差1.42倍．因此用距裂纹一定距离的位移近似解去确定相关物理量，会引起较大误差；

（2）由表1知，裂纹尖端位移场精确解可用近似解代替的条件是η=r/a≤0.2时；裂纹尖端附近的位移解与精确解相差较小，此时可以用近似解代替精确解，才不会引起较大误差．

5 结论

(1)文中基于 Westergaard函数法基本原理，推导出了裂纹尖端附近应力场与位移场在任意角度上的精确解的表达式，该表达式不受限于r≤a；

(2)裂纹尖端应力场近似解与精确解只有在r≤0.1a时，二者才能认为是等价的，否则会引起较大的误差．可以通过文中所给裂纹应力场修正系数的逼近公式对裂纹尖端附近应力场近似解进行修正，从而避免了繁琐的计算，便可以得到满足精度要求的精确解；

(3)应用修正公式，克服了只有在r≤0.2a时裂纹尖端位移场近似解才可以代替精确解的缺陷．采用文中所给的对位移场修正逼近公式，将会使确定相关物理量时可靠度和精确度得到较大的提高．

References

[1]陆毅中.工程断裂力学[M].西安:西安交通大学出版社，.1986.LU Yizhong. Engineering Fracture Mechanics [M]. Xi′an:Xi′an Jiaotong University Press,1986.

[2]董国兴. Irwin公式的成立条件和裂纹顶端的区屈服区尺寸分析[J].武汉水运工程学院学报,1986,10(1):51-60.DONG Guoxing. The fitting condition of irwin formula and the analysis of dimension of the yield zone of crack tip [J]. Journal of Wuhan University of Water Transpor tation Engineering, 1986, 10(1):51-60.

[3]杨槐堂. 裂纹尖端应力场和位移场沿θ=0°与θ=90°方向的精确解[J].浙江大学学报,1979, 5(2):66-79.YANG Huaitang. Exact solution of stress and displacement at the crack tip along the direction θ=0 and θ=90[J].Journal of Zhejiang University, 1979, 5(2): 66-79.

[4]胡卫华.I型裂纹应力场的精确解和近似解的比较[J].武汉科技大学学报(自然科学版), 2007, 30(3):327-329.HU Weihua. Comparison of accurate and approximate values of stress fields of crack I [J]. J. of Wuhan Univ. of Sci. & Tech.(Natural Science Edition), 2007, 30(3):327-329.

[5]王燮山.无限大平板I、II型裂纹尖端应力场及位移场精确解[J].浙江大学学报,1980.12(4):83-88.WANG Xieshan. Exact Solution of Stress and Displacement at the Crack Tip for Mode I、II of Infinite plate[J].Journal of Zhejiang University, 1980, 12(4):83-88.

[6]沈成康.断裂力学[M]. 上海：同济大学出版社1996.SHEN Chengkang. Fracture Mechanics [M]. Shanghai:Tongji University Press, 1996.