基于差分粒子群算法的装配式住宅项目进度优化研究

赵 平，吴 昊，李萍萍，乔媛媛

（西安建筑科技大学土木工程学院，陕西 西安 710055）

装配式建筑在施工的过程中可以改变传统建筑“湿作业”的生产方式，减少扬尘、无交叉污染、减少CO2排放、缓解日趋严重的雾霾污染问题，是未来建筑产业发展的必然趋势．但是目前装配式建筑在我国发展十分缓慢，主要的原因是装配式建筑在进度上和传统现场浇筑方式相比并没有发挥太多的优势，究其原因是施工过程各环节协调配合的问题，而解决这一问题的关键就是装配式建筑施工中的合理调度问题．

装配式建筑的调度问题，是在满足施工工序的逻辑关系和资源约束的条件下，对施工工序和资源进行合理的安排，控制好工序的开始、结束时间，以达到工期优化的目标，也就是单执行模式资源受限项目调度问题(Single-Mode Resource-constrained Project Scheduling Problem，简称SRCPSP)．虽然此类问题被证明是Np难问题[1]，但国内外学者做了大量的研究并取得了丰硕的研究成果．一般采用数学规划、动态规划[2-3]等精确算法来求解小规模调度问题的最优解；采用启发式算法，如遗传算法、模拟退火算法、蚁群算法、粒子群算法等[4-7]来求解较大规模调度问题的最优解．但是由于各个算法都存在一定的缺陷，单纯应用某一算法优化调度问题时，就会导致性能较差的结果，进行算法相结合可以实现二者之间的优势互补，提高算法优化的性能．本文提出的差分粒子群算法(DEPSO)通过差分算法(DE)弥补了粒子群算法(PSO)容易陷入局部最优和搜索精度相对较低的缺陷，并将全局优化性能较好的差分算法和收敛速度较快的粒子群算法优势结合在一起，加强两个种群间的信息融合，提高整个种群的进化能力，达到增强混合算法的求解能力．

1 问题描述和数学模型

1.1 问题描述

工程项目的施工过程属于资源约束的调度问题，资源主要分为可更新资源和不可更新资源．可更新资源是指总量虽然有限，但一旦结束某项任务开始下个任务时资源可更新为原来的总量，如：劳动力、设备等；不可更新资源是指该项资源会随着工程的开展而不断减少，如使用的原材料、资金等．

装配式住宅项目进度优化问题是以最短工期为最优目标，假设装配式住宅项目中每一项工作都只有一种执行模式，紧前工作或紧后工作的逻辑关系是确定的，要求所有紧前工作结束后，紧后工作立刻开始，执行过程没有间歇；而且不考虑不可更新资源的约束情况，只考虑可更新资源的约束，在满足各个工作之间的逻辑关系约束和资源需求约束的条件下，对各项工作的开始或结束时间进行合理安排，使工期最优[8]．

1.2 装配式住宅项目模型的建立

装配式住宅项目共包含N项工作，第一项工作1表示项目的开始工作，最后一项工作N表示项目的结束工作，是虚工作．进度控制目的是在满足装配式住宅项目工作合理搭接的前提下，通过合理安排各项工作的资源，使工期最小化．

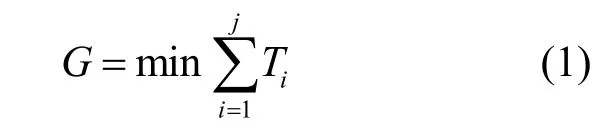
工作i的开始时间：

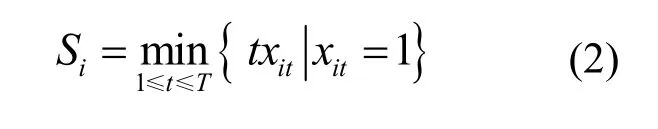
工作i的完成时间：

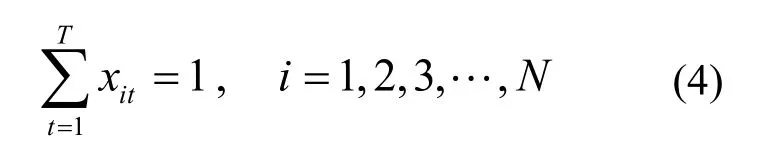
建设项目需要J种可更新资源，其中第j种资源在t时刻的供给量为要完成第i项工作需要若干种资源，其中对第j种资源的需求量rji；要求所使用的各种资源总和不能超过资源总量．项目在某一时刻对某种资源的需求不能超过该资源的供给量．则资源约束表示为：

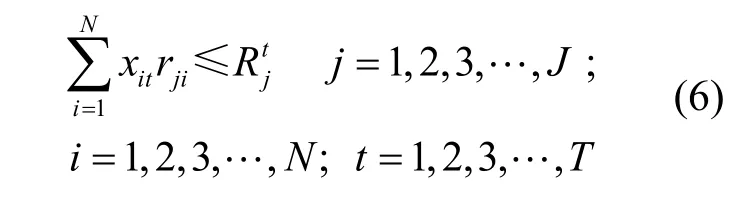
2 基于差分粒子群优化的装配式住宅项目调度算法

2.1 差分算法

差分算法主要用于求解优化最小值的问题，是从随机产生的初始群体开始，求解父代个体间随机选取的两个个体差值的基础之上与另外一个随机选取个体的加权求和生成变异种群．在父代个体和变异个体间执行交叉操作形成一个新的种群，然后通过比较由交叉算子生成的个体和相应父代个体的适应值优劣，如此反复迭代和进化，保留优良个体，舍弃劣质个体，直到找到最优解．需要注意的是整个运行过程中保持群体的规模不变．

设原始种群X包含N个候选解，定义 [1,]r∈R为空间的维度，空间内的个体，则变异个体为

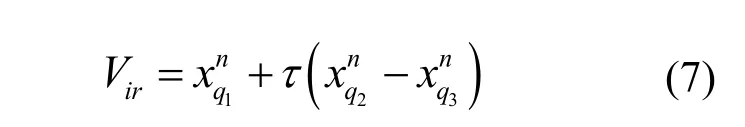
根据交叉操作由式(8)可生成新的一个种群表示为：

通过交叉后的个体Pir和父代个体的适应度值，保留较优的适应度值．

2.2 差分混合粒子群算法

粒子群算法(PSO)，是基于随机群体的一种新型智能优化方法[9]．其算法简单，易于操作，鲁棒性较强，收敛速度较快，但在求解的过程中容易陷入局部最优而且搜索精度相对较低．基于PSO不足之处，Yuhui Shi[10]对基本粒子群算法进行了优化，通过引入一个惯性权重因子ω，调整上下时刻之间速度的影响，平衡全局和局部的搜索能力，从而提高了该算法的精确性．由于ω对算法性能影响较大，一般的做法是将其开始设置较大随着迭代次数的增加而逐渐减小，通常

现定义维度为R的空间中个数为N的粒子在以一定的速度飞行，第j个粒子的位置和速度分别表示为和该粒子所经历的最好位置为全局最优位置为Q，它表示Pj中的最优值，式(9)式(10)分别表示了粒子的速度和位置更新公式．

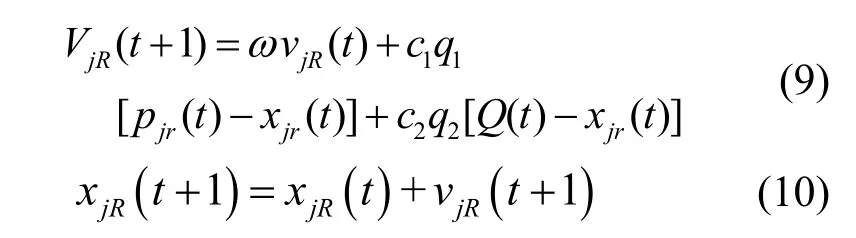
2.3 差分混合进化粒子群算法

PSO的特点是在优化求解过程中前期收敛速度较快，而在后期求解中如果没有新的粒子来更新当前最好位置时，那么群体中的其他粒子就会朝着这个当前最好位置靠近，由于粒子都集中到较小范围的区域，将会导致适应值变化缓慢或者无变化，算法就会出现停滞现象[11]．通过DE 的变异操作可以对个体的最好位置进行不断地更新，增加了全局的搜索能力，而交叉操作提高了局部搜索能力，选择操作则产生了优秀的个体．

DEPSO就是通过一种新的信息互融机制，使两个种群中的信息能够互相交流，从而避免了某些个体得到错误的判断信息而陷入局部最优点．采取非线性惯性权重策略来对权重进行改进，以进一步提高其优化性能，权重优化状态方程如式(11)．

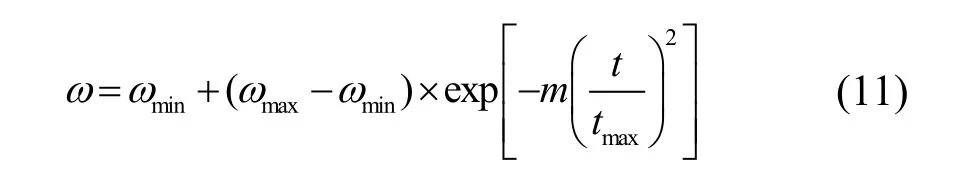
其中m为控制因子．用来控制ω与t变化曲线的平滑度，通常取3．

为了克服两个种群中的粒子在后期的迭代进化中出现停滞现象，引入一种变异机制，也就是说如果粒子在设定的最大迭代次数内出现了停滞现象即发生变异，该粒子将被任一新位置所取代，具体实现过程如式(12)．

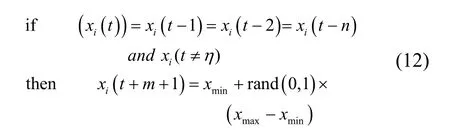
其中∶η代表适应度函数在整个种群中的最小值，m是允许停滞的最大迭代次数，是搜索的范围．

2.4 混合算法的参数设置及实现步骤

合理的设置算法的参数能更好的发挥算法的优化性能，参考Kennedy和Eberahart对PSO算法以及Price[12]对DE算法参数设置研究，本文算法基本参数设置如下:群体规模N=100、最大迭代次数最大惯性权重最小惯性权重加速因子C1=2=C2、缩放因子τ=0.5、变异概率CR=0.5、设置迭代计数器t=0．

本文提出的混合算法DEPSO实现步骤如下:

第一步：基本参数设置，群体规模N、最大迭代次数Tmax、最大惯性权重wmax、最小惯性权重加速因子C1和C2缩放因子、变异概率CR、设置迭代计数器t=0．

第二步：将群体等分成两个种群PPSO和PDE，随机产生两个粒子，初始化PPSO和PDE而且让二者位于不同的区域．

第三步：根据式(7)、式(8)对PDE群体中所有个体执行变异、交叉、选择操作．

第四步：根据式(9)、(10)和式(11)对PPSO群体中所有个体执行速度、位置更新．

第五步：通过比较适应值，选出PPSO群体中最佳个体GPSO．

第六步：通过比较适应值，选出DEP 群体中最佳个体GDE．

第七步：比较GPSO、GDE优劣，选择最佳个体作为PPSO和PDE下一代进化依据．

第八步：判断个体是否有停滞现象，如果有，按式(12)执行变异操作．

第九步：更新迭代计数器t=t+1并记录当前整个群体中最佳个体，如果满足精度要求或整个进化已达到最大迭代次数，就终止算法，输出全局最优位置的粒子并生成调度方案，否则转至第三步．

3 实例分析

现以某地某保障性住宅项目为例，本工程主体结构形式为剪力墙结构，共5幢，每幢4个单元六层，建筑面积19 225 m2，占地面积3 204 m2．单幢楼东西长63.02 m，南北宽11.02 m．层高为3 m，室内净高2.89 m．主体结构部分内、外墙板均采用预制装配式墙体，结构楼板、楼梯部分采用叠合板，楼梯、阳台均采用预制装配式形式，空调板、节点、接缝等采用现场现浇的方式．

通过将施工过程进行科学的施工组织，按楼层将其分为多个施工段．论文以其中一个施工阶段为研究对象，设定每项任务只有一种模式，在满足逻辑关系和资源的约束下，力求使项目的总工期最小，假定建设项目所需预制构件数量能满足施工要求，预制构件的运输、固定、堆放等都能保证装配施工顺利进行．

施工企业在以往的进度计划的编制过程中，采用的是Project软件，并以此作为项目的执行计划．从图1所示的工程项目网络图可以得到关键线路上的工期为2.85 d，但是在计划的编制过程中，管理者几乎没有考虑资源的约束问题，依靠关键线路得到的项目工期是不合理的．

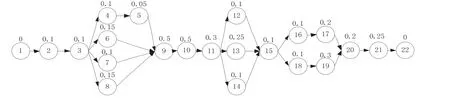
图1 项目网络图Fig.1 Project network diagram

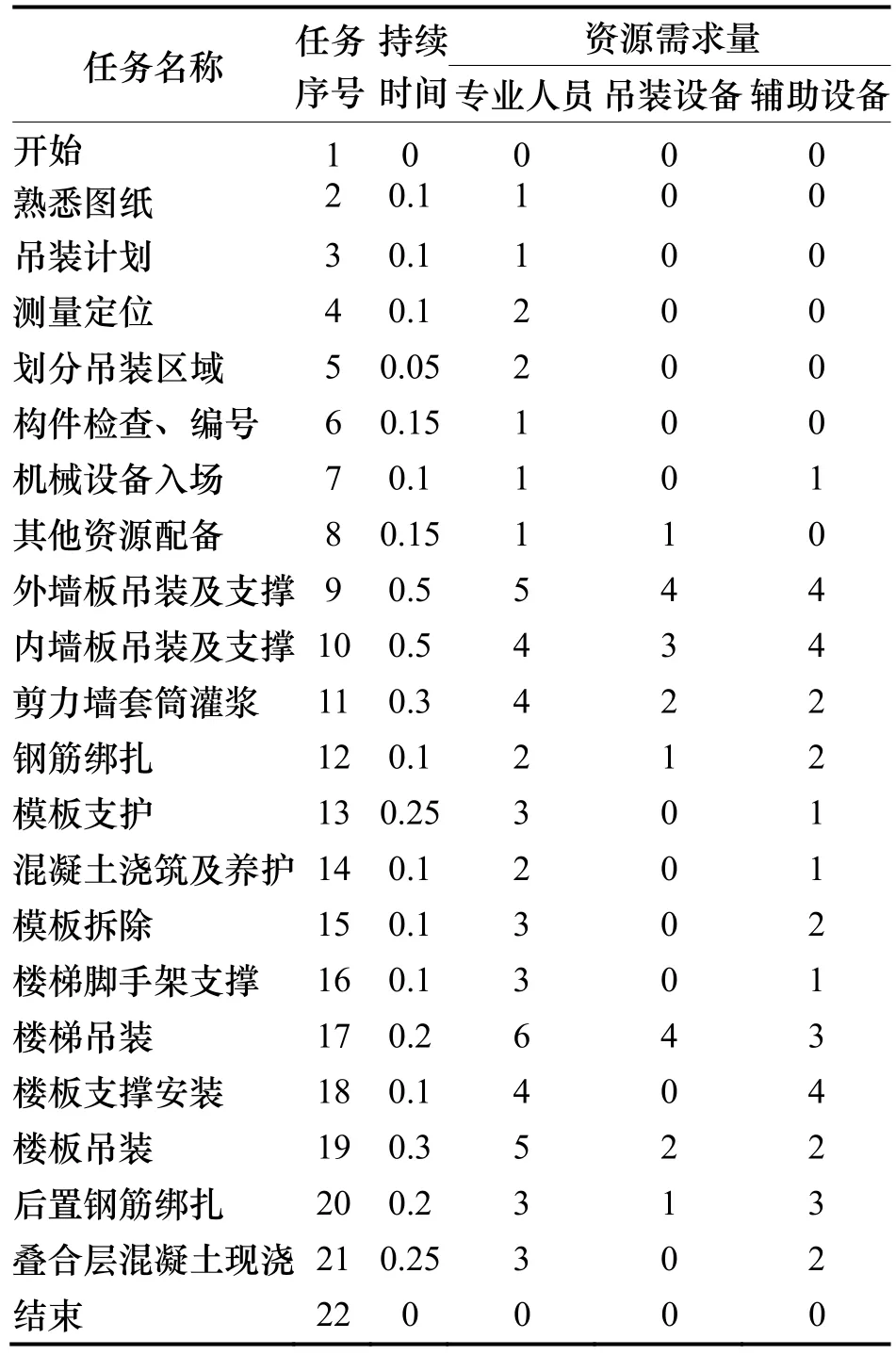
表1 项目任务信息列表Tab.1 Project task information

本工程每项工作的工期及资源需求量见表1．由于这里是以标准层为研究对象故表中前几项项工作中某些任务不需要专业的人员和设备，从表中可以看出预制剪力墙结构施工主要分为：墙体部分、现浇部分以及楼梯、楼板部分．

由于承建公司同时开展多个项目，故依据项目部的资源实际可调配情况，选取所有活动影响系数较高的3种可更新资源，分别为专业操作人员(司机、混凝土工、木工、钢筋工等)、可用吊装及其辅助设备(塔吊、电焊机、葫芦等)、其他可用设备(钢梁、钢丝绳等)．

本文采用差分算法(DE)、粒子群算法(PSO)、差分粒子群算法(DEPSO)对上述工程的调度问题进行求解，每种算法运行50次，分别求出平均工期以及工期的标准差，进而比较算法的合理性及性能的先进性．用Matlab软件实现算法并用Excel进行处理，运行结果如表2所示．

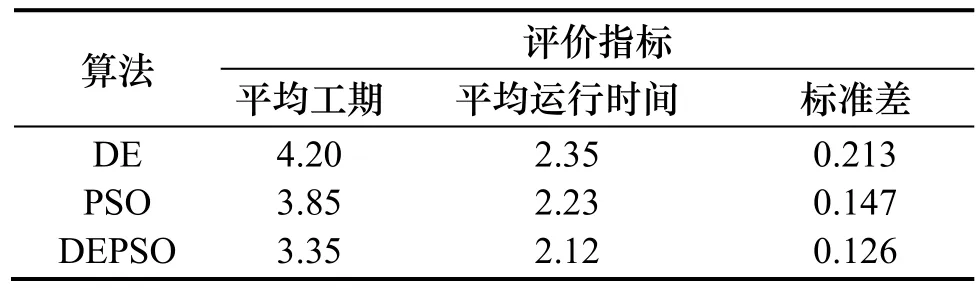
表2 算法结果对比Tab.1 The results of algorithm

从表2可以看出，三种算法均对装配式项目工期起到了优化作用，其中DEPSO在求解工期方面有较大的优势，经过多次运算后得到的平均工期为3.40 d、标准差为0.126，在三种算法中最优，DE和PSO在装配式工期优化方面效果较DEPSO差．在既有资源约束相同的情况下，通过DESPSO所得到的最优工期比同行业平均装配施工工期短，较好的实现了预期的目标，可为同类问题的进度优化提供很好的借鉴意义．

DEPSO混合算法通过加强两个种群之间的信息互融机制扩大了搜索的范围．另外，通过变异机制解决算法在迭代过程中的停滞现象，同时通过非线性惯性权重策略对其性能进行调整，使其跳出局部最优进而实现全局最优．最后得到的最优调度序列为（1，2，3，4，5，7，6，8，9，10，11，12，13，14，15，18，19，16，17，20，21，22），项目优化后的标准层工期为3.40 d．

4 结论

(1) 单一的算法在求解复杂项目的进度优化中不仅运行较慢，而且搜索全局最优解的的能力较低、求解精度不高；而通过算法的改进使其优势互补，可以提高其全局搜索能力，进而提高寻求最优解的概率．

(2) 建立的DEPSO混合算法通过在二者之间建立一种信息互融机制，使两种算法的有机结合；改进后的混合算法克服了DE收敛速度慢和PSO容易局部最优的缺陷，使得算法的性能更加合理、高效．

(3) 通过DEPSO求解构建的装配式住宅项目调度数学模型，得到了在有限资源下的最优工期，对工程实践有一定的指导作用．但装配式住宅项目优化过程中受多种资源的约束，文中只分析了影响较大的三种可更新资源，建议将受约束的不可更新资源考虑进去，使优化的结果更接近实际．

Reference

[1]KOLIS R, HARTMANN S. Experimental investigation of heuristics for resource-contrained project scheduling:an update[J]. European Journal of Operational Research,2006, 174(1):23-37.

[2]李雪, 聂兰顺, 齐文艳. 基于近似动态规划的动态车辆调度算法[J]. 中国机械工程, 2015, 26(5): 682-688.LI Xue, NIE Lanshun, QI Wenyan.Dynamic vehicle scheduling algorithm based on approximate dynamic programming [J]. China Mechanical Engineering, 2015,269(5): 682-688.

[3]黄风林,屈端,范峥.数学规划法优化氢网络的应用研究[J].化学工程,2015,43(3):70-73.HUANG Fenglin,QU Duan,FAN Zheng .Application research on mathematical programming methodology forhydrogen network optimization[J]. Chemical Engineering,2015,43(3):70-73.

[4]张光明,刘东峰,刘春峰.基于遗传算法的两阶段建筑工程多目标优化[J].西安建筑科技大学学报(自然科学版),2011,43(3):410-416.ZHANG Guangming, LIU Dongfeng, LIU Chunfeng.Comprehensive optimization for multiple objectives inconstruction based on GA[J]. J. Xi'an Univ. of Arch. &Tech. (Natural Science Edition), 2011,43(3):410-416.

[5]王秋平,史荣,张琦.基于改进蚁群算法和网络GIS分析的慢行交通最优路径选择[J].西安建筑科技大学学报(自然科学版),2013,45(5):668-674,687.WANG Qiuping, SHI Rong, ZHANG Qi. Optimal path selection of slow traffic based on GIS network analysis[J]. J. Xi'an Univ. of Arch. & Tech. (Natural Science Edition), 2013,45(5): 668-674, 687.

[6]刘海霞,李仁旺,李学.基于遗传模拟退火算法的制造网格资源调度策略[J].计算机工程与应用,2008,44(6):234-237.LIU Haixia, LI Renwang, LI Xue. Resource scheduling strategy in manufacture grid based on genetic algorithms and simulated anealing[J]. Computer Engineering and Application, 2008,44(6): 234-236.

[7]甄彤,郭嘉,吴建军.粒子群算法求解粮堆温度模型参数优化问题[J].计算机工程与应用,2012,48(12):206-208.ZHEN Tong, GUO Jia, WU Jianjun. To solve problems of mathematical model of temperature field for grain based on PSO[J]. Computer Engineering and Applications, 2012, 48(12): 206-208.

[8]刘士新.项目优化调度理论与方法[M].北京:机械工业出版社,2007.LIU Shixin. Theory and method of project optimization scheduling[M]. Beijing: Mechanical Industry Press, 2007.

[9]KENNEDY J,EBERHARTR C. Particle Swarm Optimization[C]//Proc. IEEE Int. Conf. on Neural Networks,Piscataway: IEEE, 1995: 1942-1948.

[10]SHI Y, EBERHARTR C. A Modified Particle Swarm Optimizer[C]//Proc. IEEE World Congress on Computational Intelligence, Piscataway: IEEE, 1998:69-73.

[11]池元成,方杰,蔡国飙.基于差分进化和粒子群优化算法的混合优化算法[J].计算机工程与计,2009,30(12):2963- 2965.CHI Yuancheng, FANG Jie,CAI Guobiao. Hybrid optimization algorithm based on differential evolution and particle swarm optimization[J]. Computer Engineering and Design, 2009,30 (12):2963-2965.

[12]PRICE K. An introduction to differential evolution: new ideas in optimization[M].. Maidenhead: McGraw-Hill,1999:79-1087.