结构性能概率模型的小样本建模方法

姚继涛，程凯凯，宋 璨

（西安建筑科技大学土木工程学院，陕西 西安 710055）

目前通过试验建立结构性能概率模型的过程中，一般采用经典统计学中的矩法推断其中关键的计算模式不定性系数的概率特性，并以此为基础推断结构性能的概率特性[1,2]．理论上讲，矩法仅适用于样本容量（试件数量）很大的场合[3]，而试验建模中的试件数量往往有限，很难达到大样本容量的要求，这时矩法的推断结果会受到显著的统计不定性的影响[4]，并直接影响对结构性能概率特性的推断，存在较大的因过高估计结构性能而导致额外失效风险的可能．欧洲规范在推断结构抗力设计值时建议，样本容量不大于100时应采用与经典统计学方法不同的小样本推断方法．这可作为试验建模中需考虑统计不定性影响的参考标准．但目前无论样本容量多少，均不加区别地采用了经典统计学的方法，可能因统计不定性的影响而过高估计结构的性能，导致额外的失效风险．这是目前试验建模中涉及基本方法的一个普遍问题，对结构的可靠度分析和设计都有着全局性的影响．

论文将针对目前试件数量普遍不足的现象，研究小样本条件下建立结构性能概率模型的方法，合理反映统计不定性对推断结果的影响．

1 建模的基本步骤

结构性能的概率模型一般可表达为[5]

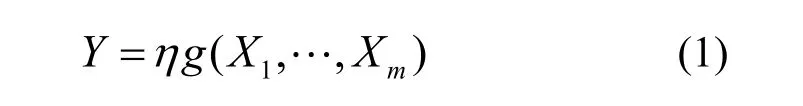
式中：g(·)为结构性能函数；X1,…,Xm为几何参数、材料性能等影响因素；η为反映尺寸效应、时间效应、环境条件、工艺条件等影响的计算模式不定性系数．这里将η分解为两部分，即

设实验室中通过n个试件的试验得到和Y的n组数据，这时建立结构性能概率模型的基本步骤如下：

(1)通过对试验数据的拟合或对理论分析结果的修正，建立结构性能函数g(·)．它一般应满足或近似满足

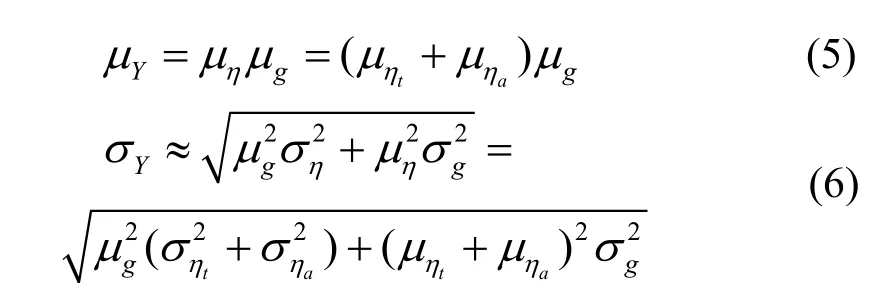
(5)确定结构性能Y的概率分布形式，最终形成完整的结构性能概率模型．一般直接假定其服从对数正态分布或正态分布[7]．

推断计算模式不定性系数的概率特性是上述建模过程中的关键步骤，这里以此为重点讨论结构性能概率模型的建模方法．

2 目前建模方法

虽然目前未明确对计算模式不定性系数η按式(2)进行分解，但其推断过程实际上包含着类似的两个步骤：根据试验结果推断实验室条件下计算模式不定性系数的概率特性；根据经验对其做适当调整，以考虑实际条件的影响．一般采用经典统计学中的矩法推断的均值和标准差，其结果分别为[1,2]

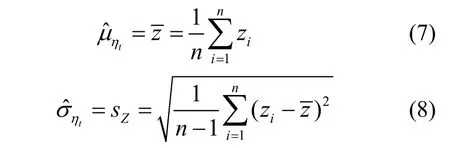
理论上讲，矩法仅适用于样本容量n很大的场合[3]，而试验建模中的试件数量往往有限，很难达到大样本容量的要求，这时矩法的推断结果会受到统计不定性的影响[4]．

所谓统计不定性指因样本容量不足而产生的推断结果的不确定性．样本容量n不足时，即使无试验误差，也不能断定均值、标准差的推断值为其真值若重复做同样的多组试验，各组的推断结果之间也往往存在差异，且样本容量越小，差异一般越大．这些均为推断中统计不定性的表现，一般可以一定置信水平下推断结果的相对误差反映统计不定性的影响．

它们亦为随机变量，且随机性越大，推断中的统计不定性越大．令它们分别为矩法推断结果可能具有的相对误差．可以证明

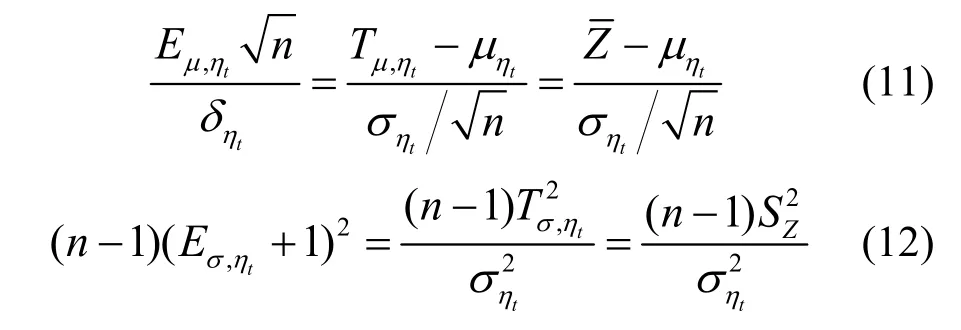
它们分别服从标准正态分布和自由度为n-1的卡方分布[8]．这时利用区间估计法[3]，可得一定置信水平下相对误差的上、下限．

图1所示为置信水平C=0.9、变异系数的典型情况下相对误差的上、下限．可见：样本容量较小时，矩法推断结果存在着较大的相对误差，受统计不定性的影响显著，且主要存在于对标准差的推断中．换言之，矩法的推断结果，特别是对标准差的推断结果，会在较大的范围内波动，存在较大的因过高估计结构性能而导致额外失效风险的可能．

图1 概率特性推断结果相对误差的上、下限Fig.1 The upper and lower value of relative error for inference result of probability characteristic for

3 区间估计法

为考虑统计不定性的影响，样本容量n较小时，宜采用较矩法保守的方法推断的概率特性，其中较常用的方法是区间估计法[3]．这时可构造统计量

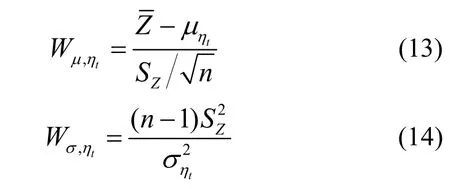
它们分别服从自由度为n-1的t分布和自由度为n- 1的卡方分布[8]．分别令

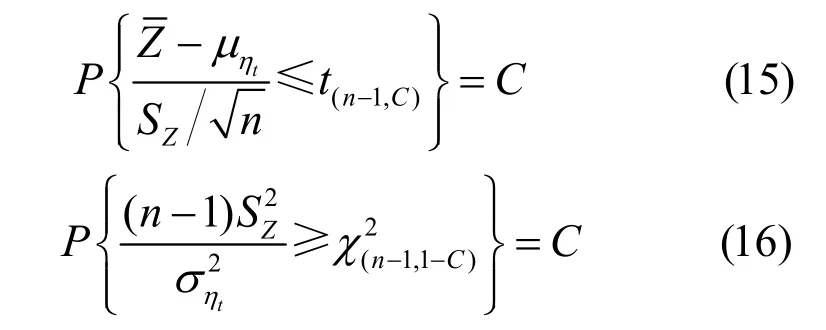
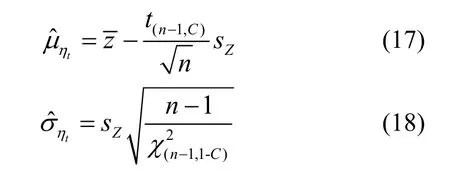
区间估计法虽可给出较矩法稳妥的结果，但推断中必须确定置信水平C，它对推断结果有着直接影响，且数值越高，影响越大．置信水平并不存在理论上的值，需依据经验选择，受主观因素的影响较大，这给建模方法的统一和建模结果的比较带来一定的困难，不便于应用．

4 贝叶斯法

贝叶斯法[9]同样可在小样本条件下给出较矩法稳妥的结果，但可回避对置信水平C的选择．这时需采取以下步骤：视计算模式不定性系数tη的概率分布为关于未知参数的条件概率分布它仍为正态分布；同时，视未知参数为随机变量，并利用先验信息确定其联合先验分布；利用贝叶斯公式，确定的联合后验分布；利用条件概率分析方法，进一步确定的概率分布据此确定未知参数的估计值．

贝叶斯推断中的关键问题是如何确定未知参数的先验分布，它不可避免地要受到主观因素的影响．在这一方面，Jeffreys提出的无信息先验分布因对未知参数的取值无任何偏爱而能够较大程度地降低主观因素的影响[10]，在贝叶斯推断中得到广泛应用．现行国际标准 ISO2394:1998[7]和欧洲规范EN1990:2002[11]中均采用了基于 Jeffreys无信息先验分布的贝叶斯法．

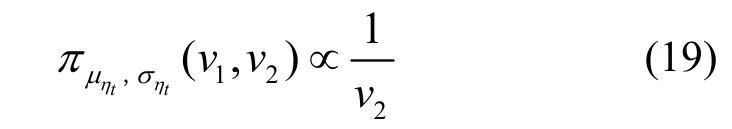
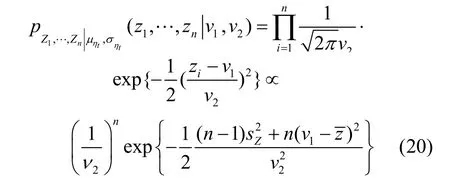
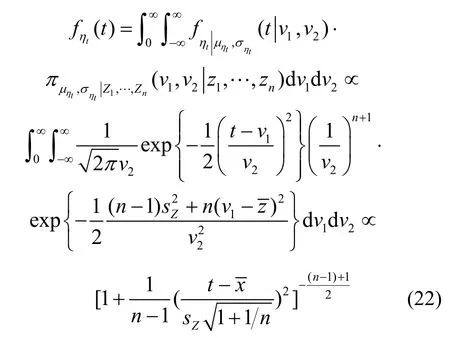
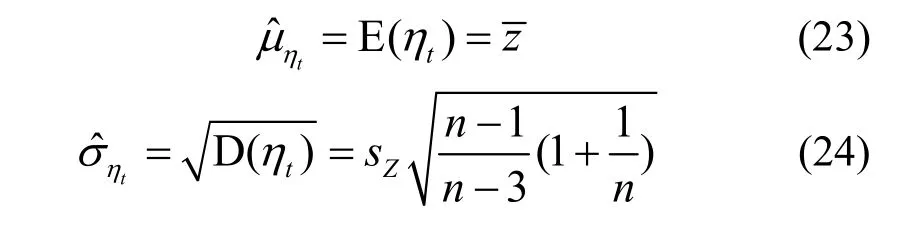
它适用于样本容量n≥4的场合，一般的试验建模中均可满足这一要求．

这里的贝叶斯法与一般的贝叶斯法存在着差别．按一般贝叶斯法[9]，在得到的联合后验分布后，则分别确定的边缘分布，并以的均值作为其估计值．根据式（21），的边缘分布分别为

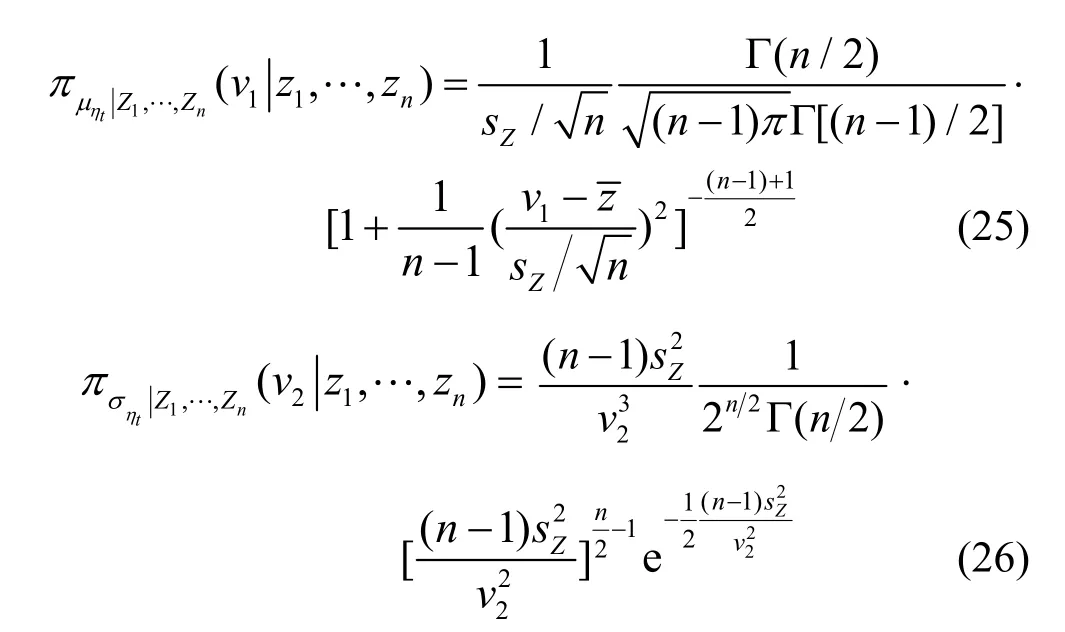
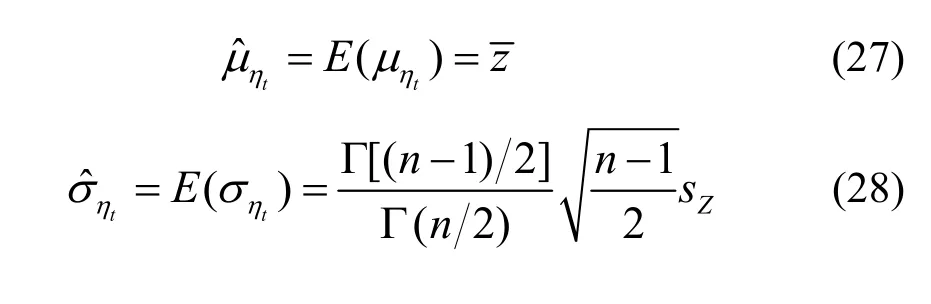
5 对比分析

5.1 统计不定性的反映程度

无论采用矩法、区间估计法、一般贝叶斯法还是本文贝叶斯法，样本容量较小时推断中的统计不定性都是存在的．矩法和区间估计法推断中的统计不定性表现为统计量的随机性，而贝叶斯法推断中的则表现为分布参数的随机性．

矩法是依据统计量的均值建立的，未充分考虑统计量的随机性，因此也不能充分反映统计不定性对推断结果的影响．区间估计法则是依据统计量的分位值建立的，置信水平较高时，其考虑统计量随机性的程度亦较高，可较充分地反映统计不定性的影响．一般贝叶斯法是依据分布参数的后验分布建立的，它以均值作为分布参数的推断结果，亦不能充分反映统计不定性的影响．文中贝叶斯法是以分布参数的后验分布为权函数，按式（22）对的条件概率分布加权平均后，依据的概率分布建立的，它考虑了分布参数所有可能的取值及其概率，这也意味着它可全面反映统计不定性对推断结果的影响；相对而言，区间估计法是局部地反映了统计不定性的影响．

5.2 推断结果的等效置信水平

矩法、贝叶斯法中虽无置信水平的概念，但隐含着等效的置信水平．令它们的推断结果与区间估计法的相等，便可确定相应的等效置信水平．例如，对于文中贝叶斯法，可令

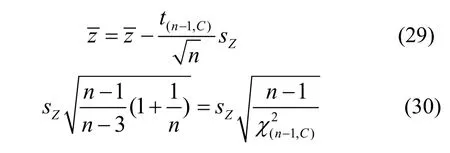
通过独立求解关于C的这两个方程，可分别确定推断结果的等效置信水平．

图2所示为矩法和贝叶斯法推断结果的等效置信水平，可见：均值推断结果的等效置信水平均为0.5；在标准差的推断中，矩法和一般贝叶斯法的等效置信水平相近，但均低于0.5，特别是当样本容量较小时；文中贝叶斯法中标准差推断结果的等效置信水平在样本容量为4～70时为0.58～0.85，且样本容量越小，等效置信水平越高．统计不定性的影响主要存在于对标准差的推断中，等效置信水平越高，对统计不定性的考虑越充分．按区间估计法的观点，标准差推断结果的等效置信水平应高于 0.5，特别是在样本容量较小时．文中贝叶斯法的等效置信水平满足这种一般性要求，但矩法和一般贝叶斯法等效置信水平过低．

图2 矩法和贝叶斯法推断结果的等效置信水平Fig.2 The equivalent confidence level of inference result for the moment and the Bayesian method

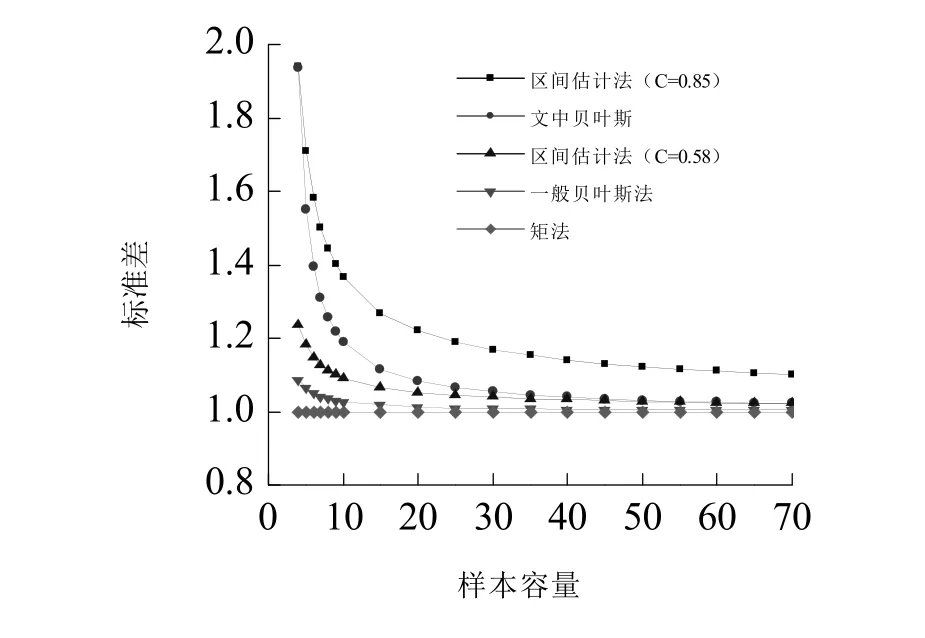
图3 各种方法中标准差的推断结果Fig.3 The inference result of the standard deviation ofvarious methods

5.3 推断结果

综上所述，文中贝叶斯法不仅回避了区间估计法中因置信水平的选择而带来的困难，更便于应用，而且可全面反映统计不定性的影响，其均值的推断结果相对准确，而标准差推断中的等效置信水平可满足一般性的要求，推断结果稳妥、适中，可作为小样本条件下建立结构性能概率模型的一个基本方法．

6 结论

推断计算模式不定性系数的概率特性是建立结构性能概率模型的关键．针对样本容量普遍不足的现象，重点研究了实验室条件下计算模式不定性系数概率特性的推断方法，结论如下：

(1) 样本容量较小时，无论采用哪种方法，推断中的统计不定性都是存在的．目前采用的矩法未充分反映统计不定性的影响，推断结果受统计不定性的影响显著，且主要存在于对标准差的推断中，相应的等效置信水平过低，推断结果偏于冒进，存在较大的因过高估计结构性能而导致额外失效风险的可能．一般贝叶斯法存在与矩法同样的缺陷．

(2) 区间估计法较充分地反映了统计不定性的影响，可给出较矩法和一般贝叶斯法稳妥的结果，特别是在样本容量较小时，但必须人为选择置信水平，受主观因素的影响较大，给建模方法的统一和建模结果的比较带来一定困难，不便于应用．

(3) 文中贝叶斯法可全面反映统计不定性的影响，其均值的推断结果相对准确，而标准差推断中的等效置信水平可满足一般性的要求，推断结果稳妥、适中，同时回避了区间估计法中的困难，更便于应用，可作为小样本条件下建立结构性能概率模型的一个基本方法．

References

[1]中华人民共和国建设部．GB/T 50152-2012 混凝土结构试验方法标准[S]．北京：中国建筑工业出版社，2012.Ministry of construction of the People’s Republic of China．GB/T 50152-2012 Standard methods for testing of concrete structures [S]．Beijing：China Architecture and Building Press，2012.

[2]中华人民共和国建设部．GB 50152-92 混凝土结构试验方法标准[S]．北京：中国建筑工业出版社，1992.Ministry of construction of the People’s Republic of China．GB 50152-92 Standard methods for testing of concrete structures [S]．Beijing：China Architecture and Building Press，1992.

[3]茆诗松，王静龙，濮晓龙．高等数理统计[M]．北京：高等教育出版社，施普林格出版社，1998.MAO Shisong，WANG Jinglong，PU Xiaolong．Advanced Mathematical Statistics [M]．Beijing：Higher Education Press，Springer-Verlag Press，1998.

[4]Alfredo H-S. Ang，Wilson H. Tang. Probability concepts in engineering planning and design (Ⅱ) [M]．New York:John Wiley & Son, Inc，1984.

[5]JCSS. JCSS probabilistic model code: part 1: basis ofdesign [S]. Copenhagen, Denmark: Joint Committee on Structural Safety, 2001.

[6]中国建筑科学研究院．建筑结构设计统一标：GBJ68-84[S]．北京：中国建筑工业出版社，1984.

China Academy of Building Research．GBJ 68-84 Unified standard for design of building structures[S]．Beijing：China Architecture and Building Press，1984.

[7]International Organization for Standardization. ISO2394:

1998 International Standard: General Principles on Reliability for Structures [S]. Switzerland : International Organization for Standardization ,1998.

[8]茆诗松，王静龙，史定华．统计手册[M]．北京：科学出版社，2003.MAO Shisong，WANG Jinglong，SHI Dinghua．Statistics handbook [M]．Beijing：Science Press， 2003.

[9]茆诗松．贝叶斯统计[M]．北京：中国统计出版社，2005.MAO Shisong．Bayesian Statistics [M]．Beijing：China Statistics Press，2005.

[10]JEFFREYS H．Theory of Probability [M]．London：Oxford University Press，1961.

[11]European committee for standardization. EN1990-2002：Eurocode-basis of structural design [S]. London, UK:BSI,2002