冻融受荷协同作用下沥青混合料损伤模型研究

张 倩，李 泽，温志广，侯振华

(1. 西安建筑科技大学土木工程学院，陕西 西安 710055；2. 包头市公路局，内蒙古 包头 014030)

寒区沥青混凝土路面常年处于正负温交变状态，在外荷载和冻融环境因素综合作用下，内部携带的各类初始微缺陷会不断萌生、发展，当累积损伤达到材料失效门槛值时，裂缝、松散和坑槽等宏观物理性能逐渐响应[1]．近年来，随着寒区基础设施工程建设不断兴起，越来越多的沥青混凝土路面冻融耦合损伤问题亟待解决．因此，建立沥青混合料冻融受荷协同损伤模型，探究其损伤劣化机制，进而提出冻融损伤后寿命预估方法，将对冻区沥青路面设计、性能评估及养护时机选择具有重要的理论价值和现实意义．

近年来，国内外众多学者对沥青混合料冻融破坏研究主要集中在环境或荷载等单因素对混合料宏观性能指标及冻融损伤特性的影响方面．AMINI等[1-3]研究了沥青混合料含水量、饱和度、含盐浓度、温度等外在因素和级配、油石比、空隙率，对其强度和模量的耐冻性能影响，Si Wei[4]考虑了温度和冻融循环对寒区沥青混合料压缩特性的影响，张倩等[5]基于冻融劈裂前后试件的 CT图像，研究了沥青混合料微观结构损伤特性，谭忆秋等[6-7]建立了沥青混合料冻融损伤本构方程，吴志勇[8]获得了与加载次数，荷载大小及劲度模量相关的幂函数疲劳累积损伤模型．文献[9-10]通过试验阐释了沥青混合料的性能冻融衰减特征及规律．事实上，寒区沥青路面损伤是多因素全方位、多层次、多角度综合作用的结果，不仅受限于材料内部不同尺度的宏细观影响，而且还有外部环境和荷载的作用．但现有大部分研究只考虑冻融或荷载等单因素作用下造成的损伤，不能真实反映沥青路面实际工作状态．尝试在冻融循环条件下研究受荷沥青混合料多因素的协同损伤问题，将是寒区沥青路面研究的热点课题．

基于损伤力学方法，借助宏观统计损伤模型，构建沥青混合料冻融受荷协同作用下损伤模型，研究冻融次数与应变对沥青混合料力学特性及损伤劣化的影响，揭示材料冻融受荷损伤演变规律，探讨不同油石比条件下冻融破坏机理，并通过冻融弯曲试验结果验证模型的合理性，以期为沥青路面抗冻融受荷设计和性能评估提供理论支撑．

1 冻融受荷协同损伤模型

1.1 沥青混合料冻融受荷协同破损机制

冻融与外荷载以不同的力学机理作用于沥青混合料微裂隙等薄弱部位相连通的损伤域，耦合效应加剧了空隙中水冰相变、水分迁移，使得荷载与材料损伤之间不断反馈调整，导致材料物理力学性能劣化失效．

考虑到沥青混合料冻结和融化的含冰混合料、水、空气等多相介质具有不同的热物理特性和缩胀率，当温度降低时，饱水混合料体积收缩，而空隙水凝冰膨胀，易引起跨集料边界缩胀失调；由于混合料的非连续特性，在集料及微空隙间产生显著的冻胀力不能得到有效传递释放而在粗集料界面附近易发生应力集中，当冻胀力超过沥青-集料界面粘结力失效阈值时会迫使内部微裂纹萌生、扩展，损伤也相继形成；当温度上升时，混合料内部凝冰开始融化，同时伴随着冻胀力的消散、迁移水对沥青-集料界面反复侵蚀．多次冻融循环后，沥青混合料累积耗散能逐渐降低，导致其物理力学性能不可逆衰减，残余寿命相继缩短．尤其在消融时段，外荷载会对混合料产生负压泵吸作用，沥青砂浆受空隙中正负动水压力反复冲刷效应加剧，进一步加速集料界面之间滑移与错动，沥青砂浆颗粒逐渐损失，集料表面沥青膜减薄；大量微裂隙、孔洞产生、扩展、汇合贯通，材料性能迅速退化，最终演化为一定尺度的宏观裂缝、剥落、松散、坑槽等病害．

1.2 冻融荷载协同损伤变量

沥青混合料经历多次冻融后内部细微观缺陷损伤规律非常复杂，表征冻融损伤的弯曲劲度模量等物理力学指标不断退化．宏观唯象损伤力学理论[11]认为，沥青混合料性能指标弯曲劲度模量的衰减能够反映材料的内部损伤程度，且在冻融受荷试验过程中便于量测和分析．因此可将沥青混合料冻融损伤变量表示为

式中：Dn为沥青混合料n次冻融后的损伤变量；En、E0分别为沥青混合料n次冻融后和冻融前初始弯曲劲度模量．

由于大多数沥青混合料碾压成型过程中皆携带初始微损伤，故将其冻融前初始损伤状态定义为基准损伤状态，根据Lemaitre提出的应变等效假设及有效应力概念，可得沥青混合料损伤本构关系为

式中：Dl为荷载作用下损伤变量．

根据张全胜等[12]推广后的应变等价原理，材料在不同损伤状态下的本构关系形式相同，只替换式(2)中的E0即可．因此将沥青混合料冻融损伤后的状态作为第一种损伤状态，冻融荷载协同作用下的损伤状态作为第二种损伤状态，从而可得损伤本构关系为

将式(1)代入式(3)，得到沥青混合料冻融荷载协同损伤本构关系为

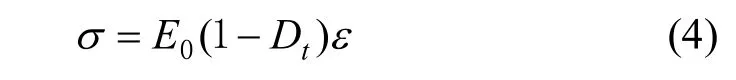
其中:

式中：Dt为冻融受荷总损伤变量，Dl Dn为耦合项．

由式(5)可以看出，总损伤变量并不等价于冻融变量与荷载变量的简单代数叠加，二者耦合效应加剧了沥青混合料的损伤程度，呈非线性递增趋势．但耦合项前的负号表示在荷载下集料颗粒的搓揉、滑移削弱了由冻融引起的内部损伤，冻胀效应得到有效缓解，使总损伤有所弱化．

1.3 冻融荷载协同损伤演化方程

沥青混合料是一种内含各类随机分布细观缺陷的非均质材料，初始携带的各类微空隙、微裂缝可视为连续分散于材料内部的一种细观结构损伤场，其损伤程度在多因素综合作用下也呈概率性分布，假设沥青混合料微元体强度服从Weibull分布，其概率密度函数[13]为

式中，ε为沥青混合料应变值；m、F为表征材料物理力学性质的参数，分别反映材料对外荷载不同响应下的统计特征，通常与模量E、泊松比υ等材料参数有关．

假定沥青混合料的损伤由局部微元体不均匀破坏引起，将某一荷载下已破坏微元体数目Nc与总微元体数目N之比定义为统计损伤变量Dl．在任意应变区间内，产生破坏的微元体数目为NP(x)dx，当加载到某一应变水平ε时，已破坏的微元体数目可表示为

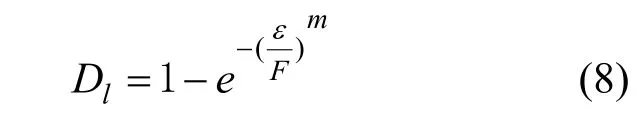
联立式(2)、(8)，根据应力-应变曲线上的峰值强度可推导确定损伤统计本构模型参数m和F分别为

由式(1)、(5)、(8)、(9)和(10)，得出以冻融次数和应变为损伤控制变量的总损伤演化方程为

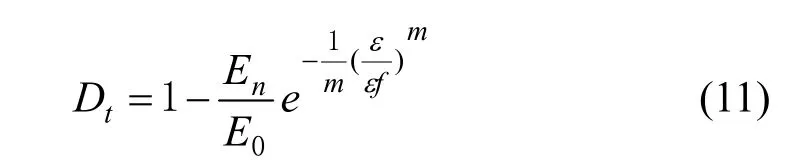
式(11)表明，当仅考虑冻融损伤时，即ε=0，则Dt=Dn；当只考虑受荷损伤时，即E0=En，则Dt=Dl．

将式(11)代入式(4)得到沥青混合料冻融受荷损伤本构方程为

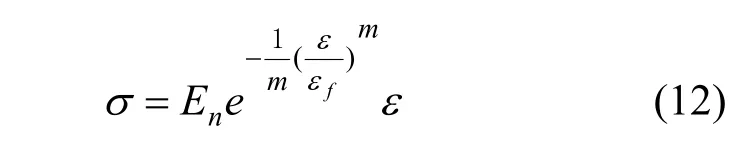
当冻融次数和受荷应变变化时，由式(1)、 (5)、(8)、(11)可得沥青混合料总损伤率演化方程为

当冻融次数恒定时，受荷损伤演化率为

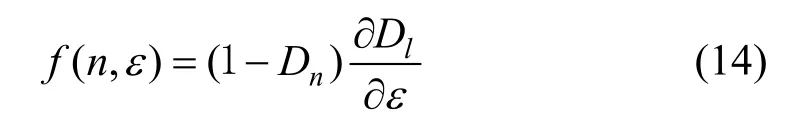
当受荷应变恒定时，冻融损伤演化率为

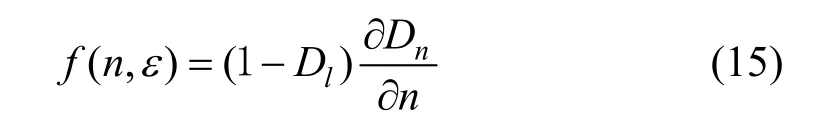
由式(13)、(14)和(15)可知，沥青混合料总损伤分别沿冻融和荷载两途径演化，揭示了冻融循环次数和应变对其损伤演变相互耦合、相互影响的特性，客观清晰地再现了沥青混合料损伤力学行为及损伤破坏规律．

2 计算实例与模型验证

文献[14]选取AC-13沥青混合料，在不同冻融循环周期下进行低温弯曲试验．其中冻融试验条件为：−20 ℃低温冷冻箱中冻结 12 h，25 ℃恒温水浴中融化12 h，利用低温冷冻箱与恒温水浴模拟冻融作用，冻结时用塑料袋密封试件，并注水30 mL，使其充分饱水．低温弯曲试验条件为：试验温度为−10 ℃，加载速率为50 mm/min．表1为AC-13沥青混合料级配组成，试验所得相关数据见表2～4，根据式(9)计算获得模型参数m见表5，图1是由式(11)计算得到的 5种油石比沥青混合料冻融受荷损伤模型演化曲线．

表1 AC-13沥青混合料级配Tab.1 Gradation of AC-13 asphalt mixture

表2 沥青混合料冻融弯拉强度Tab.2 The tensile strength of asphalt mixture under freeze-thaw conditions

表3 沥青混合料冻融破坏弯曲应变Tab.3 The ultimate tensile strain of asphalt mixture under freeze-thaw conditions

表4 沥青混合料冻融破坏劲度模量Tab.4 The limit stiffness modulus of asphalt mixture under freeze-thaw conditions

表5 冻融受荷损伤模型参数Tab.5 Parameters of damage model under freeze-thaw and loading

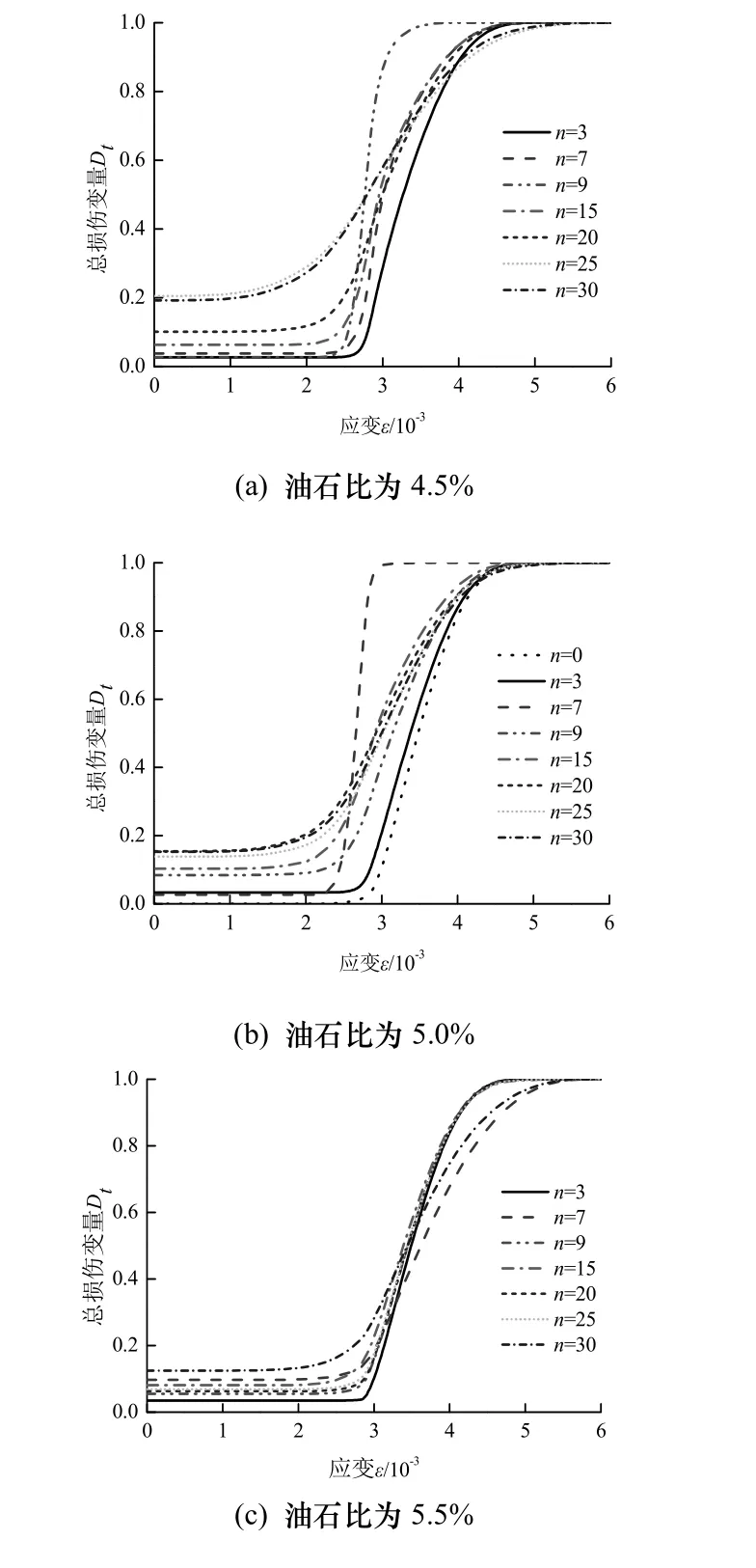
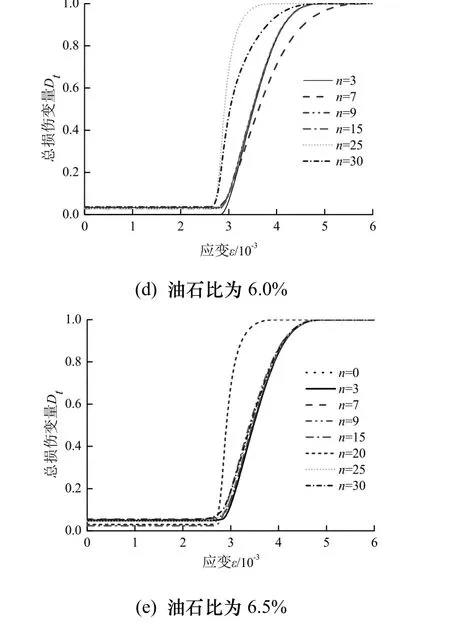
图1 沥青混合料冻融受荷损伤模型演化曲线Fig.1 Damage model evolution curves of asphalt mixture under freeze-thaw and loading

图1计算结果表明：

不同油石比条件下，沥青混合料的冻融损伤劣化随着冻融循环次数的增加而加剧，但在经历20次冻融循环后，损伤变量总体变化幅度相对较小，基本趋于恒定，表明初期冻融循环对寒区沥青混合料的抗弯拉特性影响较大．

在施荷初始阶段，当冻融次数相同时，随着油石比增加，冻融损伤程度不断得到弱化，在经过20次冻融循环后，油石比达到6.5%时，损伤变量衰减超过50%，说明沥青混合料冻融损伤程度受油石比影响显著；然而，油石比的大小又与沥青混合料的空隙率密切相关，由于冻融循环过程试件一直处于饱水状态，当油石比较低时，其内部较大的空隙完全由冰水相控制，尤其凝冰会引起内部空隙形成巨大的冻胀压力，导致混合料损伤域不断扩展断裂．随着油石比的增大，其空隙率降低，内部产生的膨胀力低于沥青-集料粘结力失效阈值，沥青混合料冻融损伤程度减缓并逐渐稳定．

冻融循环次数不变时，不同油石比沥青混合料冻融损伤劣化程度随应变的增大而加剧，这是由于受荷初期表现为损伤弱化阶段，内部微孔隙、微裂纹受压闭合，冻融产生的空隙逐渐减少，整体呈“密实”状态；当应变达到损伤阈值时，沥青混合料开始损伤演化，不断加速扩展，期间伴随着内部微裂缝的萌生、扩展、贯通，最终表现为宏观裂纹的出现，到此损伤变量趋近1，材料产生破坏．且随着油石比的加大，沥青混合料压密段逐渐变长，这与自由沥青富余有关，多余的自由沥青在集料之间发生相对滑动过程中有润滑作用，外荷载的施加，压密阶段持续时间相应延长．

图2 沥青混合料沿受荷损伤演化率分布曲线Fig.2 Damage evolution rate distribution curves of asphalt mixture along loading

图 2给出了根据式(14)计算得到的沥青混合料沿受荷损伤演化率分布曲线．由图可知，不同油石比下的沥青混合料经历相同冻融次数时，随着应变的增加，损伤率呈非线性增大趋势，达到峰值后逐渐减小．当油石比大于5.5%(最佳油石比)时，存在应变值临界区间0.002～0.002 5，若应变值小于下限，损伤率几乎为零；若应变值大于上限时，损伤率呈线性递增趋势．在最佳油石比条件下，不同冻融周期的沥青混合料损伤率较小且演化幅度大致相同，说明按最佳油石比成型的路面可改善其冻融受荷耐久性能．

沥青混合料沿受荷损伤率演化曲线特征基本一致，在峰值应变处存在最大值，但在最佳油石比时损伤率相对较小，也进一步佐证了在此状态下沥青混合料耐久性良好的观点．相较于油石比为4.5%，损伤率演化曲线峰后斜率在6.5%时较小，表明油石比较小的沥青混合料脆性破坏较显著．因此，为避免寒区沥青路面引起脆性失效，可在最佳油石比基础上适当上浮，可有效提高其抗冻融受荷破损的能力．

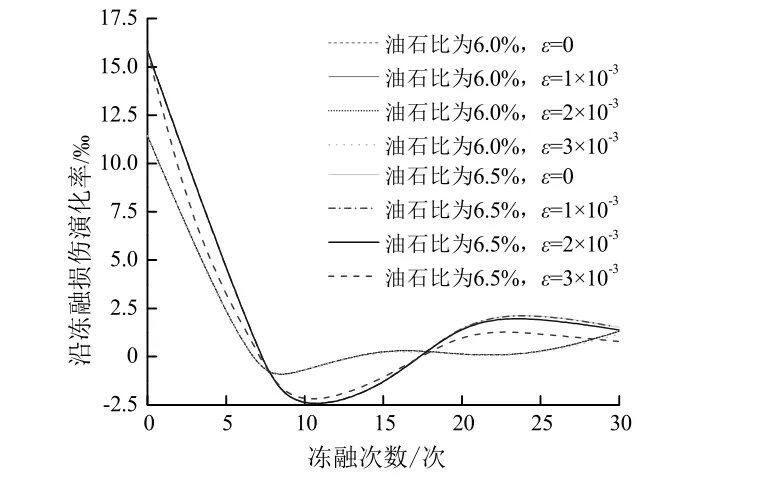
图3 沥青混合料沿冻融损伤演化率分布曲线Fig.3 Damage evolution rate distribution curves of asphalt mixture along freeze-thaw

根据式(14)和(15)计算得到沥青混合料分别沿冻融和荷载两条途径损伤演化率曲线，如图2和图3所示．当冻融次数一定时，受荷损伤率呈先增大，达到某一峰值后逐渐减小的趋势；当受荷应变恒定时，冻融损伤演化率随着冻融次数的增加逐渐减小，但在冻融次数超过 20时，无论沿冻融损伤还是沿受荷途径损伤率降低幅度都较大且基本趋于恒定．由图可知在油石比小于6.5%时，受荷应变越大，冻融损伤率贡献越小，反之亦然，说明冻融和荷载对沥青混合料损伤率的贡献变化是一个此消彼涨的过程，因此合理评估沥青混合料的冻融受荷损伤劣化程度须在特定冻融周期和实际荷载工况下进行．

图4 弯拉强度与冻融次数关系Fig.4 Relation curves between tensile strength and freeze-thaw cycles

由于不同油石比下沥青混合料冻融受荷损伤演化趋势相同，为验证不同冻融次数条件下本构方程的合理性，分别选取油石比为6.0%和6.5%的试验数据按式(12)进行计算，图 4给出了试验结果与模型计算结果．从图4可看出，两种油石比下的模型计算曲线与试验值均非常接近，吻合较好．

根据本文冻融受荷模型得到的沥青混合料损伤演化规律与文献[14]中试验现象及实际分析结论相一致．说明提出的表征沥青混合料冻融受荷的损伤本构方程和演化模型较为合理可靠．

3 结论

(1) 考虑冻融与荷载双因素协同作用，基于损伤力学分析方法，建立了表征沥青混合料冻融受荷损伤模型及演化方程，且验证了其合理性，为从细观损伤方向研究宏观冻融受荷协同破损机制提供了新视角．

(2) 冻融与荷载协同作用可使沥青混合料总损伤程度加剧，呈非线性增长趋势，但耦合效应使总损伤弱化．二者以不同的损伤机理作用于沥青混合料，使得两种损伤之间不断反馈调整，最终导致材料发生破坏．在油石比恒定条件下，沥青混合料冻融损伤变量随冻融次数的增加而增大，但在 20次之后，其值基本恒定；在冻融损伤变量不变情况下，随着冻融次数的增加，应变呈降低趋势；当应变一定时，冻融损伤劣化程度随冻融次数增加而加剧．

(3) 沥青混合料沿冻融和荷载两条途径损伤演化率曲线呈不同分布特征．沿受荷应变损伤时，损伤率呈先增大后减小趋势，存在峰值；沿冻融循环损伤时，损伤率逐渐减小并最终保持稳定，但在两种途径下损伤率在超过 20次冻融循环后降低幅度都较大且趋于恒定．

References

[1]AMINI B, TEHRANI S S. Simultaneous effects of salted water flow on asphalt concrete pavement deterioration under freeze-thaw cycles [J]. International Journal of Pavement Engineering, 2014, 15(5): 383-391.

[2]SÉBASTIEN L, DANIEL P, HERVÉ D B. Contraction and expansion of partially saturated hot mix asphalt samples exposed to freeze-thaw cycles[J]. Road Materials and Pavement Design, 2015, 16(2): 277-299.

[3]OZGAN E, SERIN S. Investigation of certain engineering characteristics of asphalt concrete exposed to freeze-thaw cycles [J]. Cold Reg. Sci. Technol., 2013（85）: 131-136.

[4]SI Wei, MA Biao, WANG Hainian, et al. Analysis of compressive characteristics of asphalt mixture under freeze-thaw cycles in cold plateau regions[J]. Journal of Highway and Transportation Research and Development,2013, 7(4): 17-22.

[5]张倩, 李创军. 沥青混合料冻融劈裂微观结构损伤特性分析[J]. 公路交通科技, 2010, 27(2): 6-9.ZHANG Qian, LI Chuangjun. Analysis of micro structural damage characteristic of freeze thaw split asphalt mixtures[J]. Journal of Highway and Transportation Research and Development, 2010, 27(2): 6-9.

[6]谭忆秋, 赵立东, 蓝碧武, 等. 沥青混合料冻融损伤模型及寿命预估研究[J]. 公路交通科技, 2011,28(6): 1-7.TAN Yiqiu, ZHAO Lidong, LAN Biwu, et al．Research on freeze-thaw damage model and life prediction of asphalt mixture[J].Journal of Highway and Transportation Research and Development, 2011, 28(6): 1-7.

[7]李兆生, 谭忆秋. 沥青混合料冻融损伤特性研究[J].中国科技论文, 2014, 9(11): 1279-1281.LI Zhaosheng, TAN Yiqiu. Research on asphalt mixture freezing-thawing damage performance[J]. China Science Paper. 2014, 9(11): 1279-1281.

[8]吴志勇. 基于多级等幅荷载下的沥青混合料损伤累积和沥青面层疲劳损伤破坏研究[D]. 广州: 华南理工大学, 2014.WU Zhiyong. Research on cumulative fatigue damage of asphalt mixture and asphalt layer based on multi-level amplitude loading[D].Guangzhou: South China University of Technology, 2014.

[9]司伟, 马骉, 任君平, 等. 基于可靠度的冻融循环下沥青路面性能[J].吉林大学学报(工学版), 2016, 46(1):126-132.SI Wei, MA Biao, REN Junping, et al. Analysis of asphalt pavement performance under freeze-thaw cycles using reliability method[J].Journal of Jilin University (Engineering and Technology Edition), 2016, 46(1):126-132.

[10]颜可珍, 游凌云, 王晓亮. SMA 混合料冻融循环性能试验及超声波法评价[J].中国公路学报,2015,28(11):8-14.YAN Kezhen, YOU Linyun, WANG Xiaoliang. Test on characteristics of SMA mixture under freeze-thaw cycle and ultrasonic evaluation method[J]. China Journal of Highway and Transport, 2015, 28(11): 8-14.

[11]李兆霞. 损伤力学及其应用[M]. 北京: 科学出版社,2002.LI Zhaoxia. Damage mechanics and its application[M].Beijing: Science Press, 2002.

[12]张全胜, 杨更社, 任建喜. 岩石损伤变量及本构方程的新探讨[J]. 岩石力学与工程学报, 2003, 22(1):30-34.ZHANG Quansheng, YANG Gengshe, REN Jianxi. New study of damage variable and constitutive equation of rock[J].Chinese Journal of Rock Mechanics and Engineering, 2003, 22(1): 30-34.

[13]张我华, 孙林柱, 王军, 等. 随机损伤力学与模糊随机有限元[M]. 北京: 科学出版社, 2011.ZHANG Wohua, SUN Linzhu, WANG Jun, et al. The stochastic damage mechanics and fuzzy-random finite element method[M]. Beijing: Science Press, 2011.

[14]虎见. 冻融循环作用下的沥青混合料力学参数研究[D].西安: 长安大学, 2011.HU Jian. Study on the mechanical parameters of asphalt mixture under the action of freeze-thaw cycling [D].Xiʹan: Changʹan University, 2011.