基于博弈粒子群算法的混流混合车间调度研究
2016-01-21鲁建厦胡海芬董巧英
鲁建厦,胡海芬,董巧英
(浙江工业大学 机械工程学院,浙江 杭州 310014)
基于博弈粒子群算法的混流混合车间调度研究
鲁建厦,胡海芬,董巧英
(浙江工业大学 机械工程学院,浙江 杭州 310014)
摘要:为了有效解决混流混合车间生产调度的全局优化问题,同时考虑部件车间、总装车间的齐套及平顺化要求,部件车间与零件车间缓存区存量控制要求,建立了以总装车间部件平顺化、部件车间齐套性和加工车间缓存区库存最小为优化指标的多目标调度模型.同时为解决多目标调度目标之间的矛盾关系,运用博弈粒子群算法进行求解.算法通过PSO对各车间按不同优化指标进行搜索求解并加入博弈理论以解决陷入单目标局部最优的缺陷,从而获得总生产系统全局最优.最后运用实例对模型和算法进行有效性验证.
关键词:混合车间;调度;齐套性;博弈;粒子群
车间调度问题是困扰学者的一类典型NP难题,由于其可以给企业带来明显的经济效益,因此引起了企业界和学术界的广泛关注.对于加工装配型企业,产品由零件、部件最后总装成成品.并且如今在多元化发展的趋势下,企业为了顺应时代的步伐更多的运用混流装配方式进行产品的装配.从之前的研究可知已有大量对于混流装配线及作业车间的单独调度研究,以及对混合车间的单目标整体研究.李平[1]研究在不确定条件下的混流装配线和作业车间的结合调度问题,建立了存在确定性吸收的调度数学模型,并且在其主动预调度的前提下建立自适应性柔性车间扰动—反应模型.将贝叶斯理论引入到不确定调度系统中,建立模型,并与原有模型对比.胡恒[2],施锦峰[3]就混流混合车间建立了模糊调度和鲁棒调度模型,并就车间的模糊或不确定信息表现在模型中,最终利用智能算法求解模型.李修琳[4]将零件、部件、产品三部分综合一起编码,并运用模拟退火和遗传算法的混合算法对在制品成本最小的目标进行计算.之前的研究虽然可以在一定程度上反应车间的情况,却不能更完整的全局的映射混合车间的生产状况.而在生产管理中,各车间都有其特点,因此进行全局考虑排产非常重要.笔者对混流混合车间进行全局的建模与优化,即可以顾及各车间的优化特点建立不同模型,又能全局的联系整个生产及装配车间.
多目标调度已有大量的研究文献,但处理各目标关系更多采用经验求权重计算方法,其局限于经验者的主观臆断,优值则会因人而异.为了使结果更加客观,运用博弈论[5]对各车间目标进行整合求解.国内外研究博弈论主要面向经济学,在生产方面研究较少,并且也只运用在单机或单条流水线中[6].Calleja[7]提出了单客户多任务及单任务多客户的单机调度问题.由于博弈论是对几个相互关联、影响的决策者的理性决策,并且对这些决策结果进行均衡研究的理论,因此即可以避免决策者的主观臆断,又能对多目标进行求解.笔者运用博弈理论来平衡混流混合车间多目标之间的矛盾关系,并求解各车间之间的纳什均衡作为最终的全局优化解.
1混流混合车间模型
混合车间一般由两部分或两部分以上不同车间组成.图1为笔者所研究的混流混合车间模型.该模型由三部分组成:第一部分为零件作业车间,第二部分为部件装配线,第三部分为总装线,各部分之间存在缓存区.
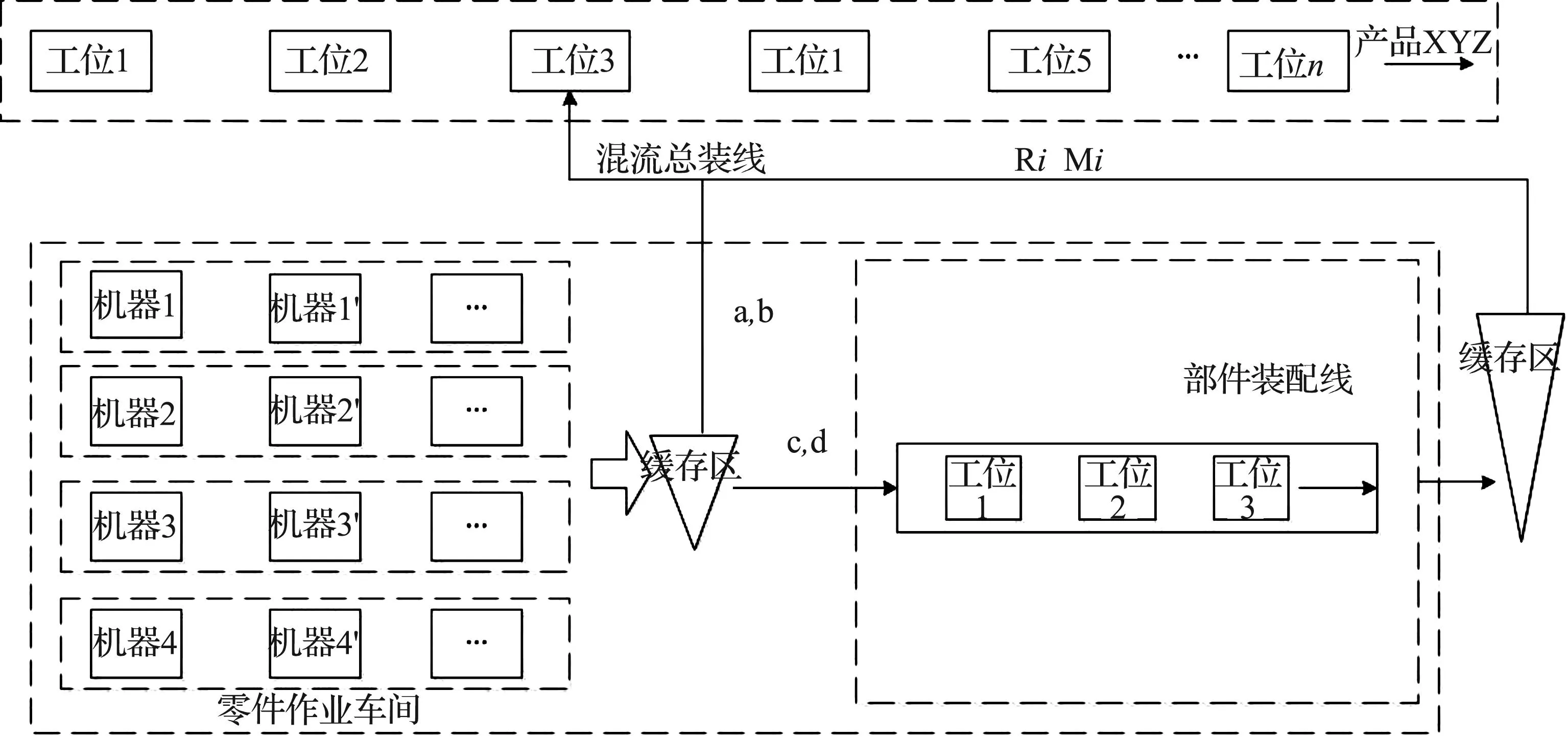
图1 混合车间模型Fig.1 Mixed-model and mixed-flow production
混合车间调度问题数学描述如下:
作业车间:有M=(m1,m2,…,mm)台机器,其中mi表示第i个机器,i=(1,2,…,m),加工r=(r1,r2,…,rr)批零件,同批零件加工工艺相同,不同批工艺由不同的事先规定的加工工艺决定;部件线:有一条具有个工位的部件线,加工个部件,每个部件需经过F道工序;总装线:包括H=(h1,h2,…,hn)个订单产品,表示第个订单产品;经过D=(1,2,…,d)个工位对产品进行装配,其中表示产品的第道工序.
混流混合车间具有的特点包括:
1) 总装线和部件线装配都是以混流的方式装配.
2) 零件作业车间、部件线、总装线之间设有缓冲区.
3) 上下游环节生产相互关联,下游装配受上游零部件加工影响.总装线需要某零部件成套时才开始总装,若装配线所需要的零部件没有及时供应,则将造成等待.
4) 混合车间生产是零件作业车间以批为单位生产零件,部件及总装线以件为单位进行混流装配,因此前后生产批量不一致将导致库存,增加成本.
2基于博弈的车间调度模型
为了客观评价多目标调度问题,解决各车间目标函数之间的矛盾关系,将博弈理论运用到混合车间调度中,并且摒弃历史研究中将加工方或者客户作为博弈的参与者,而将加工/装配区域分别抽象化为不同的局中人,并分开运算局部最优解,将最优策略以及次优策略抽象为局中人的策略空间,最优值抽象为收益函数.表1为车间调度中的元素与博弈中要素的一一映射关系.

表1 车间调度与博弈映射
2.1单条混流总装线调度模型
混流生产线的优势为减少零部件需求波动大的问题,因此零部件需求的平顺化为其特殊优化目标.设置需求平顺化即对总装线的生产序列进行合理的规划以使对零部件的需求尽量均衡,从而可以确保上游加工线中的零部件能均衡产出.根据文献[8]并考虑零部件库存,建立平顺化优化模型为
(1)
s.t.qik∈{0,1}∀i∈Ik=1,2,…,K
(2)
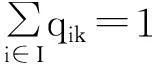
(3)
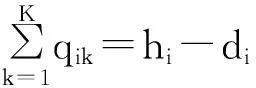
(4)

(5)
(6)
(7)
式中:qik用于判断产品i的生产位置,是0,1变量;式(3,4)分别表示序列k的位置上只会排一个产品和需要装配的产品i的数量;yik表示从1到k个产品中产品i的数量;xjk为装配yik个产品需要前工位提供j的数量;Nj为所需部件j的总数量;hi为产品i的订单需求数量;di是为i产品的库存量;bij为一个产品i需要部件j的数量;Sj为缓冲区零部件j的库存;目标函数式(1)表示最小化部件j的实际需求和平均需求的差的平方,目的尽可能使需求量与平均值相等.
2.2部件装配线调度模型

0,1判断式为
(8)
齐套系数为
(j=1,2,…,nh;1≤h≤H)
(9)
建立数学优化模型为

(10)
由于总装线目标函数求最小值,为了一致性,将式(10)处理后也求解最小值,则数学模型改为
(11)
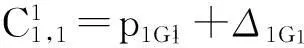
(12)
(13)
(14)
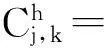
j,g∈[2,nh]i,h∈[1,H]
k=2,3,…,K
(15)
(16)
式(11)即为目标函数并且以成套订单加权和的倒数表示;式(12)表示装配序列中第一个部件在装配线上的第一个工位的完成时间;式(13)代表第一个部件在装配线其余工位的完成时间;式(14)代表序列中从第二个开始,其余部件在的第一工位完工时间;式(15)表示从序列二开始,其在部件线工位2及以后工位的完成时间.
2.3作业车间调度模型
作业车间调度问题具有工件在不同机器上加工和加工顺序不同的特点,因此可以简单描述成:存在n个零件和M台机器,每个零件已知有Yx道工序,且每道工序对应的机器和时间都是定值,其调度就是如何安排零件生产顺序和工序间隔,使调度目标最优.本节以准时制生产为目标,最小化上游零件完成时间和下游需求时间之差.
数学模型表示为
(17)
s.t. Cxtk-Cx(y-1)h≥txyk,1≤x≤n,
1≤y≤Yx,1≤k,h≤M
(18)
Chjk-Cgdk≥thjk,1≤h,g≤n,
1≤j,d≤Yx,1≤k≤M
(19)
Cxyk=max(C(x-1)gk,Cx(y-1)h)+txyk
1≤i≤n,g,j∈[1,Yx],k,h∈[1,M]
(20)
式中:Cxyk表示零件x的第y道工序在机器k上的完成时间;txyk表示零件x的第y道工序在机器k上的加工时间;Cx为零件x被加工出来的完工时刻;Tx表示零件x被领走的下游工序的开始时刻;式(18)即表示工件x的加工时间约束,需要在第y-1道工序完工以后才可以加工第y道工序;式(19)表示机器k的资源约束,即在k上不能加工不同的工件,需要一个完成后才能加工.
3调度模型求解算法设计
多目标问题的解往往有多个,并且存在难以决策的情况.通常在实际问题上可以通过优化者对该问题的了解和偏好来选择最优解,但存在主观臆断,结果并不理想.通过一个博弈理论将主观因素量化为可计算、可分析因素,并将其融入普通粒子群算法中,设计了博弈粒子群算法用于求解多目标混合车间调度问题.
3.1基本粒子群算法
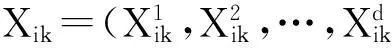
Vi,j(t+1)=ωVi,j(t)+c1×r1×[pbest(i,j)-xi,j(t)]+
c2×r2×[gbest(j)-xi,j(t)]
(21)
xi,j(t+1)=xi,j(t)+Vi,j(t+1)
(22)
式中ω为惯性权重,ω越大则全局搜索能力越强,时间也越长.如果设置的ω较小则局部搜索能力增强,时间减少.因此,可以引入动态惯性权值ω为
(23)
式中:ωmax为最大惯性权重,一般取0.9;ωmin为最小惯性权重,一般取0.4;kmax为最大迭代次数;k为当前迭代次数.c1,c2为粒子学习因子,用于调节粒子向个体及全局极值点方向飞行的最大步长,可以设置c1=c2=2.r1、r2为在(0,1)内变化的随机数.对于粒子群算法中的速度V应设置其取值范围[Vmin,Vmax]以防止粒子速度过大而超出粒子搜索范围或速度过小而早期收敛,位置Xi的取值范围为Xmin~Xmax.
3.2博弈粒子群算法
由第2节介绍可知:各车间优化目标之间会产生矛盾关系,只用普通PSO算法无法客观求得整体调度最优解,而各车间之间的矛盾关系与博弈理论中不同局中人之间的博弈关系相似,因此笔者提出增加博弈理论的博弈粒子群算法(Gameparticleswarmoptimization,GPSO)来求解混流混合车间的最优排序问题.博弈粒子群算法是在普通PSO算法的基础上,将每次迭代产生的粒子抽象为不同的策略,也代表不同解.每一次群体更新都会产生多个策略,在每一次迭代更新过程中,各个局中人都会希望将收益函数最高的策略保留下来.但各局中人之间都相互联系和影响,因此,局中人A的最优策略可能会使局中人B产生较差的结果,即对于各局中人的不同决策,会产生不同的结果.而纳什均衡即达到一个所有决策者都可接受的稳定的较优解,任何一个决策者不改变自己的决策,其他决策者只要改变就会造成收益的减少.
算法在每次种群更新的过程中都会产生各种群(局中人)的博弈,每个粒子代表博弈的纯策略,各粒子在其策略空间内搜寻最优的策略,并将最优策略用于博弈.在重复博弈中,各局中人根据纳什均衡特点对其策略进行调整以达到各局中人都满意的解.在算法的每次迭代更新中,粒子群中各粒子会向纳什均衡解的同伴粒子进行学习,通过学习,不同局中人中的粒子会调整各自的策略使粒子趋向最终纳什均衡[11].
3.2.1编码方案设计
参考遗传编码中的编码方式,数字代表各工位.其中编码方式分为两种,对于总装车间和部件车间的编码方式可以根据产品数量比例确定生产循环后用最小生产循环的产品序列进行编号,其维度为产品数量.其中相同数字代表同种产品,其粒子xp=(x1,x2,…,xn)代表总装线或部件线的产品排序.例如投产A,B,C种产品分别为2,1,2个,则其编码为Xp=(1,1,2,3,3)对于零件车间粒子的策略(加工)信息可以用一个L维向量来表示,L=n×m,其中n和m分别表示工件和机器数量.xp=(x1,x2,…,xn×m)编号代表不同零件以及各零件的加工顺序,比如编码(1 1 2 3 3 2)代表先生产零件1的第一个工位和第二个工位再生产零件2的第一个工位和零件3的第一个工位,可知相同数字代表同种零件且按顺序确定工位号.
由于寻优目标是工件的最优排序,因此需要粒子更新改变工件的顺序,但是实际上PSO算法迭代更新的都是分量的值.因此需要加入一个位置向量Y=(Y1,Y2,…,Ym)每次以工件排序为初始值,经过迭代后所得结果即为位置向量,并将位置向量进行从小到大排序即为工件排序.
例如经过一次迭代结果见表2.
通过排序:1(1.8)<2(2.7)<1(3.3)<3(3.5)<3(3.9)<2(4.1)<2(5.2)<1(6.6),这样可以得到一个可行解.Xp={1,2,1,3,3,2,2,1}为了防止产生非法解,对迭代产生粒子的顺序进行约束条件检验.对于违背约束的粒子进行位置修正.

表2 某粒子向量初始值及迭代值
3.2.2算法描述
Step 1给出粒子群规模N,速度Vmax,最大迭代次数Tmax,Pareto解集上限2,ωmax,ωmin.并初始化每个粒子的位置X和速度V.
Step 2根据之前的编码方法对各分量进行排序,生成有序的调度可行方案.
Step 3对调度方案进行解码,计算粒子适应度值,比较第一次迭代产生的适应值确定最好的为全局最优值gbest,具研究的目标函数来看,最优值为最小值;第一次迭代的各粒子适应值分别为其局部最优值pbest.具体解码过程以总装线为例表述如下:
1) 给每个粒子分别设置向量:Tk,Nj,n,Naverage.从粒子向量中顺序读取第K个产品,查找产品零部件j的需求,记录入Nj,同时根据加工时间确定第k个产品需要部件j的时刻并查找库存在Tk时刻的部件j的数量sj再与Naverage相减,将平方差值录入N.顺序读取下一个产品,将各零件所需的值和缓存区该零件的值与平均值的平方差再加入到N中直到最后一个产品处理结束.N即为该粒子的适应值.
2) 计算所有粒子适应值,N最小为当前最优粒子,将最优粒子与全局最优值比较,若小则替换gbest,并置换Pareto解集中的解;若大则保持原gbest,如果相等则作为Pareto解集中的一个解保留下来.如果此代粒子Pareto解集中只有一个解则在粒子群中查找次优粒子备用.
根据不同目标函数对部件线和零件作业车间按相同方法解码并获得全局最优和局部最优,再将总装线、部件线和零件线作为博弈对象进行三人博弈,并用划线法求得纳什均衡解分别赋值于gbest,pbest.
Step 4根据公式(21~23)进行迭代以及速度和位置的更新.
Step 5确定是否到达迭代次数Tmax,没达到则继续Step 2,直到迭代第Tmax次,输出全局最优值.
其中可以将博弈的伪码描述如下:
定义变量:
COUNT(组合策略)//COUNT表示博弈比较中该组合较优的次数
N//表示总比较次数
INPUT:各局中人的不同策略相互组合所得的每个局中人的收益值;策略组合数
OUTPUT:纳什均衡解//各车间全局极值
Begin:
For1toN
总策略数中取两种策略组合进行对比
If<所对比策略组合中的策略有且只有一个不同>then
比较不同策略所对应的收益值的大小
元素收益值小者所在的COUNT(组合策略):=COUNT(组合策略)+1
End
End
取COUNT(组合策略)值最大的策略组合为纳什均衡解
End
4实例验证
为了验证博弈粒子群算法对混流混合车间多目标调度问题求解有效性,选择以多产品加工企业的混合车间为例进行调度运算.
实例为加工A,B,C三种产品且加工量分别为2,4,2台.其中A产品需要一个零件a和一个部件M;B产品需要一个零件b和一个部件R;C产品需要一个零件c和一个部件W;一个部件M需要一个零件d;一个部件R需要一个零件e;一个部件W需要一个零件f.表3为产品所需零部件对应表.

表3 产品所需零部件对应表
表4,5为总装产品A,B,C对应的工艺及作业时间和部件M,R,W的装配工艺及时间.其中总装线工序1时分别需要零件a,b,c,工序3时分别需要部件M,R,W;部件线工序2时需要零件d,e,f.
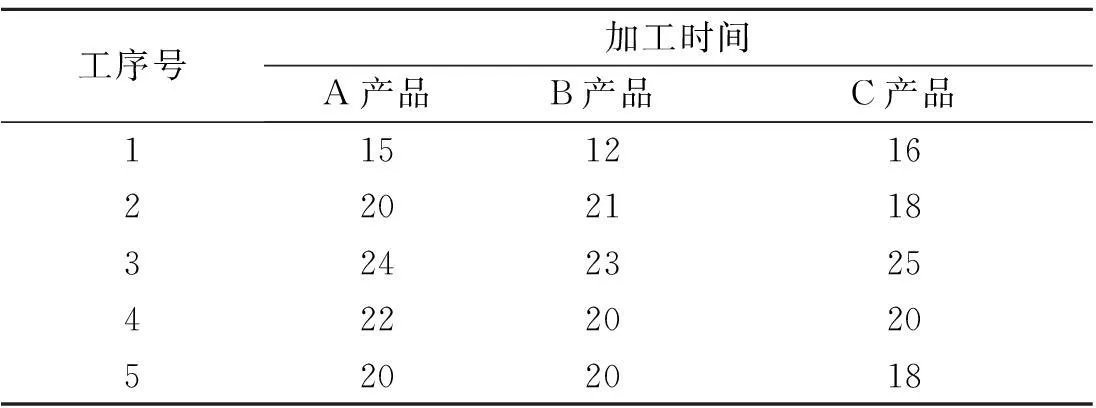
表4 总装装配工序及时间

表5 部件装配工艺及时间
自制件在机器上的加工以2个为一批进行加工,表6为其工艺顺序、加工时间和所对应机器.

表6 零件加工工位及对应时间
表7为按3.2.1编码方案进行的编码,数字1代表a零件,2和3代表b零件以此类推.根据已知条件A,B,C的产量分别为2,4,2台,其最小生产循环为1︰2︰1,因此可以对其进行初始化为(12 13 13 14 12 13 13 14).根据已知条件同时可以知道部件线所需部件M,R和W分别为2,4,2个,则其最小生产循环为1︰2︰1,可以初始化为(9 10 10 11 9 10 10 11).零件区域所需a,b,c,d,e,f零件分别为2,4,2,2,4,2 个.按批量为2来生产零件,则其零件最小循环为1︰2︰1︰1︰2︰1.按照之前的编码标准进行编码并运用PHP语言对目标及算法进行编程计算.设置初始值分别为种群大小20,迭代次数100次,最大速度为10.根据给定条件运行博弈粒子群算法求得零件、部件和总装调度方案分别为{5 6 8 5 1 6 5 1 2 7 8 6 5 2 1 8 6 7 1 7 8 2 4 3 4 2 7 3 4 4 3 3};{9 9 10 10 11 11 10 10};{12 12 13 13 14 14 13 13}.其总完工时间为360,图2为用Matlab画出零件甘特图.
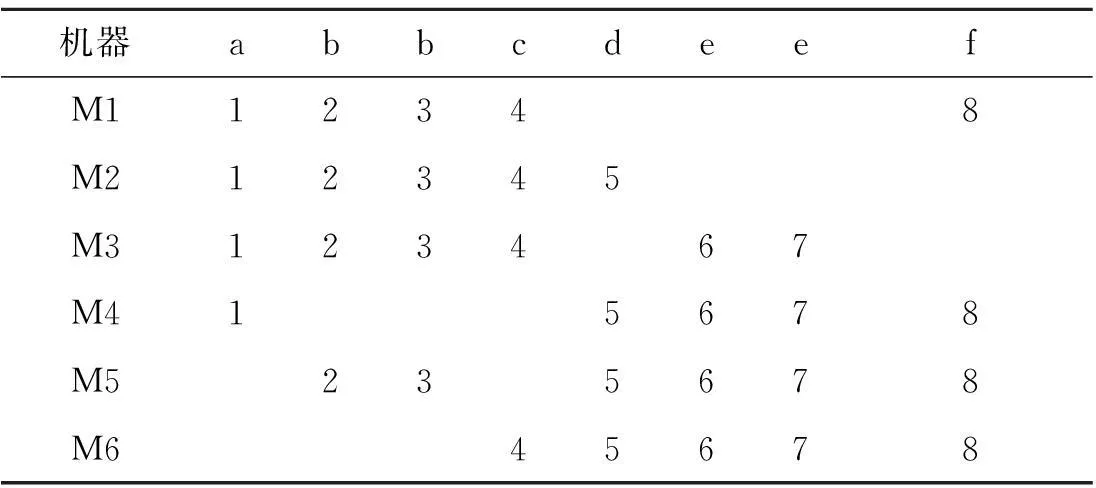
表7 实例中的工序编号

图2 零件甘特图Fig.2 Parts Gantt
通过顺序求解各车间最优序列以对比笔者算法的优越性,并求得零件、部件和总装调度方案分别为{1 5 6 2 1 6 1 5 8 2 6 2 4 6 5 1 8 4 2 8 5 7 3 3 8 4 7 3 4 7 3 7};{10 10 9 11 9 11 10 10};{13 13 12 14 13 13 12 14}.其总完工时间为386.
分别用博弈粒子群算法与顺序求解粒子群法,求得零件、部件和总装生产最大完工时间对比仿真结果,如表8所示.GPSO求解与顺序PSO求解所得结果的偏差为
通过表8对比结果可以看出:顺序PSO在零件部分和部件部分可以得到比GPSO算法更优,但在总装部分没有GPSO算法优.通过对结果的分析,得出GPSO可以对总体进行一个寻优,而作为混流混合车间更需要整体的协调和求整体较优解.
5结论
以总装车间平顺化、部件车间齐套性和零件车间缓存区最小为调度模型,极大的考虑了各车间的不同生产特点.在求解算法选择上,以基本粒子群算法分别迭代各车间,同时运用博弈论对各车间迭代结果进行评价选择.博弈粒子群算法即具有粒子群算法的规则简单优点又克服了其陷于局部最优的缺点.最后通过一个实际算例来验证算法与模型的有效性.所研究的混流混合车间调度问题极大的贴近现实生产,所设多目标优化比各学者历史研究更能体现混流混合车间特性.实例中使用的PHP脚本语言计算为之后混流混合车间调度在bs架构下的原型系统设立奠定基础.
参考文献:
[1]李平.不确定条件下混装和作业车间调度问题研究[D].武汉:武汉科技大学,2013.
[2]胡恒,鲁建厦,李英德,等.基于多群体并行遗传算法的混流混合车间模糊调度研究[J].浙江工业大学学报,2012,40(5):554-558.
[3]鲁建厦,施锦峰,李修琳,等.一类已知概率分布下的混合车间鲁棒调度问题研究[J].中国机械工程,2012,21(19):2328-2333.
[4]李修琳,鲁建厦,柴国钟,等.基于混合遗传算法的混流混合车间协同调度问题[J].中国机械工程,2012,23(8):935-940.
[5]TIJS S, DEIESSEN T, Game theory and cost allocation problems [J]. Management Science,1986,32(8):1015-1028.
[6]周艳平.基于博弈理论的多目标生产调度问题研究[D].上海:华东理工大学,2012.
[7]CALLEJA P, ESTEVEZ-FERNANDEZ A, BORMP. Job scheduling cooperation and control[J].Operations Research Letters,2006,34(1):22.
[8]王炳刚.混流加工/装配系统集成优化研究[J].机械工程学报,2010,46(17):114-121.
[9]周水银,陈荣球.单机加权成套订单数遗传算法研究[J].系统工程.2005,23(5):22-24.
[10]韩冬梅,王丽萍,吴秋花. 基于模糊偏好的多目标粒子群算法在库存控制中的应用[J]. 浙江工业大学学报,2012,40(3):348-351.
[11]李晓,金寿松,冯定忠,等. 基于合作博弈托盘租赁联盟收益分配的研究[J]. 浙江工业大学学报,2012,40(1):84-87.
(责任编辑:陈石平)
Game theory and particle swarm optimization for mixed-model
hybrid-shop scheduling problem
LU Jiansha, HU Haifen, DONG Qiaoying
(College of Mechanical Engineering, Zhejiang University of Technology, Hangzhou 310014, China)
Abstract:The paper focused on solving the scheduling global optimization problem for mixed-model hybrid-shop, which consider the request of complete kit part consumption and the inventory control of buffer zone between job shop and Flow shop,then three objectives are given: minimizing the total variation in parts consumption in the assembly line, complete kitting of parts in the part line and minimizing buffer in the job shop. Then the GPSO algorithm is used to solve the problem of contradiction among the multi-objective scheduling objectives. The algorithm can use PSO to search local optimum of each part then the game-theory try to solve the problem to get the global optimum. Finally, an example was given to test the model and algorithm, and the results prove the method is effective and excellent.
Keywords:hybrid-shop; scheduling; complete kit; game theory; PSO
文章编号:1006-4303(2015)04-0398-07
中图分类号:TP301
文献标志码:A
作者简介:鲁建厦(1963—),男,浙江余姚人,教授,博导,研究方向为精益生产、生产调度和制造业信息化,E-mail:ljs@zjut.edu.cn.
基金项目:浙江省自然科学基金资助项目(LQ14E050004, LY12E05021)
收稿日期:2015-03-05